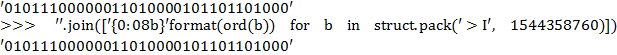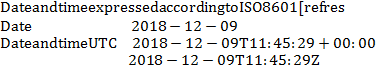- Код статьи
- S042473880003983-0-1
- DOI
- 10.31857/S042473880003983-0
- Тип публикации
- Статья
- Статус публикации
- Опубликовано
- Авторы
- Том/ Выпуск
- Том 55 / Номер 1
- Страницы
- 116-125
- Аннотация
единое времяво всех космических кораблях Человечества во Вселенной, включая Землю — как один из таких космических кораблей. В статье изложены фундаментальные принципы математического, стандартного 13-месячного эталонного зодиакального календаря.
- Ключевые слова
- стандартный Медлера—Менделеева—Морозова календарь; стандартный 13-месячный эталонный календарь; сингулярная точка времени «1 января 2013 г. (2013-I-01 00:00:00.000000000)»; ошибка запаздывания (отставания) в коде учета времени ISO 8601; космическое общество — шестая общественно-экономическая формация Цивилизации; геоцентризм; космоцентризм; астроцентризм; единое время во всех космических кораблях Человечества во Вселенной.
- Дата публикации
- 21.03.2019
- Год выхода
- 2019
- Всего подписок
- 98
- Всего просмотров
- 2206
- ГЕЛИАКАЛЬНЫЙ ГОД ЗВЕЗДЫ СИРИУС — ЭТАЛОННЫЙ ПРИРОДНЫЙ ХРОНОМЕТР ЕГИПЕТСКИХ ЖРЕЦОВ
Годичный (годовой) цикл звезды Сириус имел особое значение в Древнем Египте. Жрецы заметили, что 295¼ суток звезда Сириус хорошо видна в Северном полушарии на широте Мемфиса, но затем 70 суток она видна только в Южном полушарии Земли. Ее очередное первое циклическое появление в Северном полушарии в лучах восходящего утреннего Солнца после 70 суток отсутствия оказалось исключительно стабильным. Этот годичный цикл звезды Сириус получил научное название гелиакального года звезды Сириус. Для сельского хозяйства Древнего Египта восхождение этой звезды имело исключительное значение, так как оно удивительно коррелировало, как с разливом реки Нил, так и с началом тропического года Солнца.
Тропический год Солнца составляет промежуток времени, равный промежутку времени между двумя последовательными солнцестояниями на тропике (Рака или Козерога). Он вычисляется математически, исходя из базового, сопряженного с ним исторически гелиакального года звезды Сириус. Это был трехсезонный (каждый сезон продолжительностью четыре месяца) египетский календарь со следующими сезонами (периодами): 1) разлива реки Нил и посева ячменя и пшеницы, 2) уборки урожая, 3) засухи.
Звезда Сириус в течение 295¼ суток была хорошо видна в Северном полушарии. Затем на 70 суток она исчезала из поля зрения наблюдателей, перемещаясь из Северного полушария в Южное, и снова появлялась в лучах восходящего Солнца (т.е. гелиакально) в Северном полушарии, знаменуя таким образом новый годовой цикл.
Гелиакальный год звезды Сириус составлял ровно 365¼ суток (295¼ суток + 70 суток = 365¼ суток = 365 (32/128) суток = 365,25 суток = 365 суток 6 часов).
Этот природный астрономический феномен был очень стабильным в течение нескольких тысячелетий. Это был уникальный по точности эталонный природный хронометр египетских жрецов, который давал им абсолютную власть над населением Египта. Жрецы, благодаря своим уникальным астрономическим знаниям, точно предсказывали дату начала разлива реки Нил и связанных с этим событием начало всех сельскохозяйственных работ.
Речь идет именно о гелиакальном годе Сириуса, продолжительность которого на протяжении многих тысячелетий была равной 365,25 суток (365 суток 6 часов) с точностью до ± (1÷1,5 секунды). По расчетам выдающегося австрийского астронома Теодора Оппольцера (1841—1886)1, стандартный гелиакальный год Сириуса был равен:
в 4236 г. до н. э. — 365 суток 5 часов 59 минут 46 секунд,
в 2776 г. до н. э. — 365 суток 6 часов 00 минут 08 секунд,
в 1318 г. до н. э. — 365 суток 6 часов 00 минут 43 секунды,
в 139 г. н. э. — 365 суток 6 часов 01 минут 29 секунд.
В 46 г. до н.э. гелиакальный календарь звезды Сириус был перенесен из Египта в Рим легендарным Гаем Юлием Цезарем, где до него не было египетского 12-месячного трехсезонья звезды Сириус, но были четыре тропических 3-месячных сезона звезды Солнца.
Сезонный тропический год звезды Солнца (365 (31/128) = 365,2421875 суток) оказался на 1/128 суток короче гелиакального года звезды Сириус, что обнаружили впервые в 325 году н.э. на Никейском соборе, когда расчетная дата весеннего равноденствия в календаре переместилась на трое суток (46 + 325 = 371/128 = 2,898 ≈3 суток): с 18 марта 46 г. до н.э. на 21 марта 325 г. н.э. При этом астрономическое равноденствие реально никуда не сдвигалось. Такой неточный для годового цикла звезды Солнца расчетный юлианский календарь звезды Сириус нуждается в солнечной коррекции:
(365 32/128 суток) — 1/128 суток = (365 + 31/128) суток = 365,2421875 суток.
Поэтому после коррекции в цикле 128 лет солнечного тропического года получился 31 високосный год и 97 невисокосных лет (31 + 97 = 128 лет), вместо 32 високосных и 96 невисокосных в базовом расчетном юлианском календаре (32 + 96 = 128 лет) гелиакального года звезды Сириус. Таким образом, точность расчетного тропического календаря после коррекции регулируется вставными, високосными, годами с частотой 31/128 = 0,2421875 суток, т.е. 5 часов 48 минут 45 секунд, или 20 925 секунд. Иными словами, ошибка расчетного тропического календаря по отношению к реальному тропическому астрономическому году после математической процедуры коррекции равна нулю. Коррекция имеет идеальный по точности усредненный характер. Это чисто математическая процедура в полной аналогии с теоретической математической фазой Луны у евреев в их лунно-солнечном календаре патриарха Гиллеля II, введенной им в 359 г. н.э.
Перечень всех 31 високосных лет (перечислены в табл. 1) в первом 128-летнем цикле (2012 + 128 = 2140 год). В високосном году к Новому году будут отнесены 29- и 30-й день Козерога и 1-й день Водолея (правило 30 дней Козерога). Для этих 31 високосных лет будет использоваться один и тот же високосный календарь.
Таблица 1. Перечень 31 високосных лет
| [2016 | 2020 | 2024 | 2028 | 2032 | 2036 | 2040 | 2044 | 2048 | 2052] | ||
| [2056 | 2060 | 2064 | 2068 | 2072 | 2076 | 2080 | 2084 | 2088 | 2092] | ||
| [2096 | 2100 | 2104 | 2108 | 2112 | 2116) | 2120 | 2124 | 2128 | 2132 | 2136 | 2140] |
В табл. 2 рассчитаны все невисокосные годы (97 простых лет) в первом цикле (2012 + 128 = 2140 год). На все эти 97 невисокосных (простых) лет будет использоваться один и тот же невисокосный календарь. В невисокосном году к Новому год будут отнесены 2 дня — 29 Козерога и 1 Водолея (правило 29 дней Козерога).
Таблица 2. Перечень 97 невисокосных лет
| (2013 | 2014 | 2015) | (2017 | 2018 | 2019) | (2021 | 2022 | 2023) | (2025 | 2026 | 2027) |
| (2029 | 2030 | 2031) | (2033 | 2034 | 2035) | (2037 | 2038 | 2039) | (2041 | 2042 | 2043) |
| (2045 | 2046 | 2047) | (2049 | 2050 | 2051) | (2053 | 2054 | 2055) | (2057 | 2058 | 2059) |
| (2061 | 2062 | 2063) | (2065 | 2066 | 2067) | (2069 | 2070 | 2071) | (2073 | 2074 | 2075) |
| (2077 | 2078 | 2079) | (2081 | 2082 | 2083) | (2085 | 2086 | 2087) | (2089 | 2090 | 2091) |
| (2093 | 2094 | 2095) | (2097 | 2098 | 2099) | (2100, 2101 | 2102 | 2103) | (2105 | 2106 | 2107) |
| (2109 | 2110 | 2111) | (2113 | 2114 | 2115) | (2117 | 2118 | 2119) | (2121 | 2122 | 2123) |
| (2125 | 2126 | 2127) | (2129 | 2130 | 2131) | (2133 | 2134 | 2135) | (2137 | 2138 | 2139) |
- МАТЕМАТИЧЕСКАЯ АРХИТЕКТУРА ПОСТОЯННОЙ УНИВЕРСАЛЬНОЙ 13-МЕСЯЧНОЙ ЗОДИАКАЛЬНОЙ КАЛЕНДАРНОЙ МАТРИЦЫ
Идеальное ядро предлагаемой универсальной календарной матрицы состоит из 364 суток, 52 недель по 7 суток каждая (табл. 3). В каждом из 13 месяцев, которые имеют названия созвездий эклиптических зодиаков Солнца: I) Водолей, II) Рыбы, III) Овен, IV) Телец, V) Близнецы, VI) Рак, VII) Лев, VIII) Дева, IX) Весы, X) Скорпион, XI) Змееносец2, XII) Стрелец, XIII) Козерог), содержится ровно по 28 суток. Каждый из четырех кварталов содержит 91 день.
В обычном году имеются дополнительные 365-е сутки. В високосном году имеется дубль — дополнительные сутки — 366-е сутки. После каждого дополнительного 365-го дня в обычном году, и после каждого дубликата дополнительного 366 дня в високосном году, — календарная матрица возвращается в исходное состояние — обратно, на начало года (синхронизация реального года с идеальным). Поэтому каждый Новый год всегда постоянно начинается с 1-го дня Водолея, в воскресение.
Мы рассматриваем календарь как обычный математический цифровой счетчик времени. Из табл. 4 следует, что дни недели в традиционных календарях (в нижнем ряду каждой клетки календарной матрицы) подвижны: на начало каждого обычного года они сдвигаются на один день недели вперед, а начало каждого високосного года — сдвигается сразу на два дня недели вперед при неизменности и постоянстве самих цифровых рядов относительно друг друга: верхнего универсального и нижнего текущего.
Во всех современных календарях все происходит наоборот: постоянной является сетка Дней недели, а переменной величиной — сдвиг числовых рядов относительно друг друга — на один день в обычном году и на два дня — в високосном году.
В астрономическом плане это преобразование полностью эквивалентно в относительных параметрах. Но экономический эффект от него оказывается противоположным. Следует выбирать что-то одно: либо переменные ряды цифр при постоянной сетке дней недели, либо постоянные ряды цифр при переменной сетке дней недели.
Предлагаемые нами постоянные ряды цифр дней календаря при переменной сетке дней недели (в нижней, текущей, шкале календарной матрицы) имеют важнейшие кардинальные преимущества в экономическом плане перед постоянной сеткой дней недели и переменными рядами цифр, принятыми сегодня повсеместно во всех календарях мира.
Таблица 3. Универсальная постоянная 13-месячная календарная матрица (матрица: 13 месяцев, 52 недели по 7 суток, 8 выходных в месяц)
| Дни недели | Месяцы | |||||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | XIII | ||
| Водолей | Рыбы | Овен | Телец | Близнецы | Рак | Лев | Дева | Весы | Скорпион | Змееносец | Стрелец | Козерог | ||
| Январь | Февраль | Март | Апрель | Май | Июнь | Июль | Август | Сентябрь | Октябрь | Змееносец | Ноябрь | Декабрь | ||
| Воскресенье | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Понедельник | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| Вторник | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |
| Среда | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| Четверг | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| Пятница | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | |
| Суббота | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | |
| Воскресенье | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | |
| Понедельник | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |
| Вторник | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |
| Среда | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | |
| Четверг | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | |
| Пятница | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | |
| Суббота | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | |
| Воскресенье | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | |
| Понедельник | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | |
| Вторник | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | |
| Среда | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | |
| Четверг | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | |
| Пятница | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | |
| Суббота | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | |
| Воскресенье | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | |
| Понедельник | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | |
| Вторник | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | |
| Среда | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | |
| Четверг | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | |
| Пятница | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | |
| Суббота | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 (364) | |
| Воскресенье | 29 (365) | |||||||||||||
| Понедельник | 30 (366) |
Примечание. 14-й день Льва — дата Николы Тесла (абсолютный центр математической календарной матрицы, середина года, середина июля (Лев)).
Источник: Морозов, 2013.
При постоянных рядах цифр в календарной матрице постоянного календаря и, соответственно, при переменной сетке дней недели в нижней текущей шкале постоянного календаря, — даты деловых встреч, расписания в школах и университетах, даты школьных каникул, сетевые графики, производственные планы, длительностью более года, биржевые и банковские расчеты и т.д. будут оставаться идентичными из года в год и не потребуют, как это имеет место сейчас, никаких ежегодных перерасчетов.
Верхний универсальный (абсолютный) ряд цифр календарной матрицы в каждой клетке никогда не меняется. Он уникален и един для всех вариантов календарей. Ему взаимно однозначно соответствует свой постоянный уникальный день недели верхнего ряда календарной матрицы. Эти даты неизменны, абсолютны и постоянны — они математически едины. Это позволяет привести к единому математическому знаменателю любые конкретные календарные системы, которые размещаются во втором (нижнем) ряду каждой клетки календарной матрицы (табл. 4).
Таблица 4. Водолей
| Воскресение | Понедельник | Вторник | Среда | Четверг | Пятница | Суббота |
| 1 Водолей UM 2019 Новый год (1 января VG) вторник | 2 (2 января) среда | 3 (3 января) четверг | 4 (4 января) пятница | 5 (5 января) суббота | 6 (6 января) воскресение | 7 (7 января) понедельник |
| 8 (8 января) вторник | 9 (9 января) среда | 10 (10 января) четверг | 11 (11 января) пятница | 12 (12 января) суббота | 13 (13 января) воскресение | 14 (14 января) понедельник |
| 15 (15 января) вторник | 16 (16 января) среда | 17 (17 января) четверг | 18 (18 января) пятница | 19 (19 января) суббота | 20 (20 января) воскресение | 21 (21 января) понедельник |
| 22 (22 января) вторник | 23 (23 января) среда | 24 (24 января) четверг | 25 (25 января) пятница | 26 (26 января) суббота | 27 (27 января) воскресение | 28 (28 января) понедельник |
Примечание. Верхний ряд цифр — универсальная постоянная абсолютная дата (UM, или УД), вместе с постоянной абсолютной сеткой дней недели. В скобках указана обычная текущая ватиканская григорианская дата (VG, или ГД), последняя строка ячейки — переменная текущая сетка дней недели.
Источники: Морозов, 2018б, 2018в.
Предлагаемый в этой статье стандартный 13-месячный эталонный календарь теоретически является самым точным в истории. Он также идеально подходит для обслуживания всех известных клерикальных систем. Его ошибка по отношению к среднему тропическому году равна нулю («0»). Им удобно и предельно просто пользоваться. Он разбивает числовую ось истории на равномерные однотипные циклы — по 128 лет каждый — и содержит два ряда цифр: 1) верхний (постоянный) универсальный; 2) нижний (текущий) обычный григорианский. Запись даты производится двумя числами: 1) универсальным (УД, или UM); 2) в скобках — обычным, григорианским (ГД, или VG).
Пример 1. 1 Водолея 2020, воскресение (УД) (1-й день Января 2020, среда (ГД))».
Предлагаемый в этой статье стандартный 13-месячный эталонный календарь стабилен. Каждый Новый год всегда начинается с одной и той же даты и с одного и того же дня недели. Он позволяет иметь один и тот же универсальный день во всем мире (верхняя шкала цифр в каждой клетке календарной матрицы). Предлагаемый постоянный календарь дает неоспоримую экономическую выгоду, которая исчисляется триллионами долларов в глобальном масштабе. Это — экономия десятков тысяч тонн бумаги, красителей, типографских и транспортных расходов. Минимальный оценочный прогностический годовой экономический эффект (МОГЭЭ) от отказа от непроизводительных расходов при внедрении предлагаемого единого трафаретного стандартного 13-месячного календаря можно рассчитать по формуле:
МОГЭЭ = 5 × 10-5 × у = 5 × 10-5 × (1502,692x — 2964609,455) млрд долл.,
где y — расчетное значение мирового ВВП, x — год (линейная корреляционно-регрессионная модель). Коэффициент корреляции модели равен 0,953. Коэффициент детерминации равен 0,9093. Непроизводительные мировые затраты суммарно составляют приблизительно $0,5—1,0 трлн .[≈0,4-0,8% от мирового ВВП].
Постоянный календарь идеален при использовании в медицине и пилотируемой космонавтике, при расчетах блокчейнов и операций мировых криптобирж, в астронавигации и астродинамике (Морозов, 2018а, 2018б).
Особую популярность предлагаемый 13-месячный календарь получит в связи с тем объективным обстоятельством, что в каждом месяце он содержит стабильно по 28 суток. Это обстоятельство делает его идеальным календарем для женщин, востребованным в практической медицине у половины населения всего Земного шара, которое составляют примерно 5 млрд женщин.
На каждый цикл в 128 лет используется всего два типа (шаблона) календаря: високосный и невисокосный (простой), которые сами между собой отличаются только числом дней, относящихся к Новому году (три дня в високосном году — правило 30 дней Козерога и два дня в невисокосном году — правило 29 дней Козерога. Во всем остальном оба календаря абсолютно идентичны.
- ПОСЕКУНДНАЯ ТАРИФИКАЦИЯ КАЛЕНДАРНЫХ РАСЧЕТОВ
В табл. 5 показано, что в астронавигационных расчетах часто используют оценку продолжительности экваториального (равноденствующего) астрономического года (промежуток времени между двумя последовательными равноденствиями: осенними или весенними) по Ньюкому (1900)4. Его значение превышает фактическую длительность тропического года на ≈ 1,08 ± 1,23 секунды в год. И даже эта ошибка повышает риски космических инцидентов при баллистических расчетах и космических скоростях.
Таблица 5. Посекундное соотношение расчетов продолжительности года в различных календарях в сравнении с длительностью тропического года звезды Солнце
| Календарный год | Число суток | Секунд в году |
| Юлианский (гелиакальный год звезды Сириуса) | 365,25 = 365¼ = 365 100/400= 365 32/128 | 31 557 600 |
| Григорианский | 365,2425 = 365 97/400 | 31 556 952 |
| Невисокосный | 365 | 31 536 000 |
| Високосный | 366 | 31 622 400 |
| Астрономический (равноденствующий) средний год Солнца по Ньюкому (1900) (по точкам весеннего или осеннего равноденствия на экваторе) | 365,2422 = 365 132/545 = 365,2422018 | 31 556 926,08 = =31 556 926,23 |
| Экспериментальное определение длительности среднего равноденствующего года Солнца (1900 г.) | 365,24219878 | 31 556 925, 974592 |
| Экспериментальное определение продолжительности среднего тропического года Солнца (2015 г.): 365 суток, 5 часов, 48 минут, 45 секунд (365,2421875 суток = 365 31/128 суток) 5 | 365,2421875 = 365 31/128 | 31 556 925 |
| Теоретический расчет длительности среднего тропического года Солнца (по точкам солнцестояния на тропике Рака или Козерога) | 365,2421875 = 365 31/128 | 31 556 925 сек = = 31 556 925 × 109 наносекунд |
- УНИВЕРСАЛЬНЫЕ КОМПЬЮТЕРНЫЕ АСПЕКТЫ ОПЕРАЦИЙ И ХРАНЕНИЯ МИРОВОГО ВРЕМЕНИ ПРИ ИСПОЛЬЗОВАНИИ ТЕХНОЛОГИИ БЛОКЧЕЙН
Для хранения данных криптовалютных токенов Bitcoin используется двоичная система счисления, выраженная 4-байтовым (32 бита — 32 двоичных цифры) беззнаковым (т.е. без знака плюс или минус) целым числом. При этом максимально представимая дата в таком значении заканчивается 6 января 2106 г.
Для хранения данных о криптовалютных токенах Etherium используется 32-байтовое беззнаковым целое число (256 бит). Максимально представимая дата в таком значении в 2^224 раз больше, чем у биткойна:
В качестве нулевой точки отсчета для блокчейнов и криптовалют сейчас используется григорианская дата 1 января 1970 г., счет времени от нее ведут посекундно. Средняя ошибка григорианского календаря составляет 27 секунд каждый год.
Пример 2. Дата 1 января 1971 г. составляет 31 536 000 секунд (см. табл. 5, невисокосный год — 365 суток).
Пример 3. Дата Sun Dec 9 15:32:40 MSK 2018 в секундах составляет 1 544 358 760 секунд и выражается в 32 битах как:
C 2107 г. потребуется объем уже в размере 33 бит информации.
Пример 4. Для представления следующей даты 2110-12-09T13:05:17.442971 с точностью до микросекунд потребует уже 64 бита информации:
Если применить для хранения данных “Timestamp” 8-байтное (64 бита, т.е. 64 двоичных цифры) беззнаковое целое число, то в таком случае максимально представимый диапазон времени включает не только один полный цикл на оси времени, размером в 128 лет, в наносекундах (109), а четыре таких цикла по 128 лет каждый, т.е. охватывает период в 512 лет:
За 48 лет (с 1970 по 2018 г.) ошибка запаздывания (отставания) в машинном двоичном коде учета времени во всем мире, основанном на григорианском календаре, уже составила 1296 секунд:
Величина этой ошибки постоянно нарастает по всем расчетам в двоичном коде во всех компьютерных сетях по всему миру.
Вместо принятой сегодня стандартной нулевой точки отсчета, которая начинается с 1 января 1970 г. по григорианскому календарю (имеющему среднюю ошибку в 27 секунд в год), мы предлагаем взять за новую точку отсчета мирового компьютерного времени (в наносекундах) безошибочную универсальную нулевую точку отсчета, которой является начало текущего 128-летнего цикла — с 1 января 2013 г. (2013-I-01 00:00:00.000000000) — и абсолютное значение годового периода в размере 31 556 925 × 109 наносекунд. Это полностью соответствует данным нижней графы табл. 5 (36531/128 = 365,2421875 суток = 31 556 925 × 109 наносекунд).
Это и есть предлагаемый нами стандарт времени для новой (шестой) общественно-экономической формации космического общества (стандарт календаря Медлера—Менделеева—Морозова).
13-месячный календарь космического государства Асгардии6, который начал функционировать с 1 января 2017 г., легко вписывается в предлагаемую стандартную 13-месячную эталонную матрицу с дифференциалом в четыре года. Это — принципиально новый алгоритм и новая базовая платформа для проведения любых безошибочных глобальных операций со временем в истории: его учета и хранения, начиная с гипотетического момента Большого взрыва.
Для отображения отрезка времени, расположенного перед нулевой точкой отсчета, используется знаковое (со знаком “+” или “–”) 128-битное или любое, еще большее, целое число, например, удовлетворяющее условиям решения задач теоретической физики, в том числе, датировки времени гипотетического Большого взрыва, охватывающее суммарно какое угодно наперед заданное число лет в наносекундах в любом направлении счета времени от сингулярной точки 1 января 2013 г. (2013-I-01 00:00:00.000000000).
Как частный случай предложенную разработку можно использовать для создания любой криптовалюты (например, Солара космического государства Асгардии).
- СУЩЕСТВУЮЩИЙ ГРИГОРИАНСКИЙ СТАНДАРТ ВИЗУАЛИЗАЦИИ ФОРМАТА ДАТЫ И ВРЕМЕНИ — ISO 8601
Стандарт визуализации формата даты и времени (компьютерной метки времени) необходим во всех случаях, когда нужна максимально подробная расшифровка даты времени создания информации. Она всегда требуется в тех случаях, когда потребуется “вернуться назад”, т.е. однозначно получить обратное число секунд (например, для коррекции, для внесения изменений пользователем; обновления баз данных и пересчетов).
Распространенным сегодня решением универсальной визуализации даты и времени в григорианском календаре (который содержит теоретическую и практическую ошибку в расчетах в размере отставания от тропического года на 27 секунд в год) является стандарт ISO 8601 (год, месяц, день, час, минута, секунда (и доли секунды)) (дни недели в стандарте ISO 8601 отсутствуют; разделение на високосные и невисокосные годы тоже отсутствует):
YYYY-MM-DD-T- hh:mm:ss; YYYY-MM-DD-T- hh:mm:ss±hh:mm; YYYY-MM-DD-T-hh:mm:ss.sss (ms — точность в миллисекундах).
В нем используется метка “Z” для времени по UTC (Coordinated Universal Time = Greenwich Mean Time/GMT) или ±hh:mm для других часовых поясов.
- ВАРИАНТ ЕДИНОГО НОВОГО СТАНДАРТА МЕТКИ ВРЕМЕНИ С УЧЕТОМ РАЗНИЦЫ МЕЖДУ ВИСОКОСНЫМИ И НЕВИСОКОСНЫМИ ГОДАМИ
где
(I) — маркер: високосный / невисокосный (Leap year/Not Leap);
(II) — год: Асгардиианский (Менделеева);
(III) — месяц зодиака, римскими цифрами от I до XIII;
(IV) — день месяца от 1 до 28, в XIII месяце: Extra Day (экстра-день –«365» сутки обычного года) 29, Extra Day Duplicate (дубликат экстра-дня – «366» сутки високосного года) 30;
(V) — время — часы: мин: сек — с точностью до наносекунд;
(VI) — часовой пояс: UTC или поправка на часовой пояс.
Введение нового стандарта визуализации формата даты и времени постоянного календаря Медлера—Менделеева—Морозова имеет следующие преимущества по отношению к существующему стандарту ISO 8601:
1) точность: ликвидируется ошибка запаздывания (отставания) в машинном двоичном коде учета времени во всем мире;
2) универсальность: с первого взгляда понятен момент времени с точностью до наносекунд;
3) постоянство: время однотипно прописывается раз и навсегда во всех космических объектах Вселенной;
4) глобальность: не конфликтует с национальными календарями;
5) конвертация: может выступать инструментом-конвертером между парами любых календарей благодаря точно прописанному математическому взаимоотношению с каждым из них.
Приложение
Компактное отображение постоянного универсального 13-месячного календаря в виде одной математической таблицы-матрицы
| День недели | Месяц: I —XIII | Экстра-дни года, обычного (ED) Високосного (EDD) | |||
| 1 | 1 | 8 | 15 | 22 | ED 29 EDD 30 |
| 2 | 2 | 9 | 16 | 23 | |
| 3 | 3 | 10 | 17 | 24 | |
| 4 | 4 | 11 | 18 | 25 | |
| 5 | 5 | 12 | 19 | 26 | |
| 6 | 6 | 13 | 20 | 27 | |
| 7 | 7 | 14 | 21 | 28 |
Библиография
- 1. Морозов С.Л. (2013). Об одной новой календарной системе // Экономика и мате-матические методы. Т. 49. № 4. С. 111—125.
- 2. Морозов С.Л. (2018а). Гомеостатический ковчег и эталонный постоянный календарь Д.И. Менделеева как главные средства в стратегии индустриализации космоса и создания космического общества. Монография. М.: ООО «Ваш формат».
- 3. Морозов С.Л. (2018б). Менделеевский эталонный календарь России на 2019 год. Монография. М.: ООО «Ваш формат».
- 4. Морозов С.Л. (2018в). Менделеевский эталонный календарь России на 2020 год. Монография. М.: ООО «Ваш формат».
- 5. Сухова С. (2018). Эталона года как не было, так и нет. Экономист объяснил Свет-лане Суховой, какой календарь нужен современному человечеству? // Огонёк. № 49 (5544). С. 26—27.