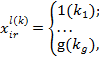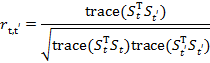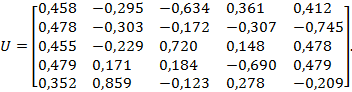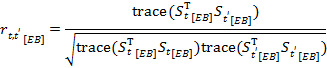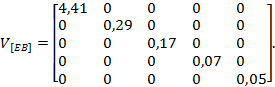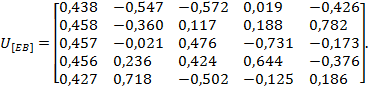- Код статьи
- S042473880004678-4-1
- DOI
- 10.31857/S042473880004678-4
- Тип публикации
- Статья
- Статус публикации
- Опубликовано
- Авторы
- Том/ Выпуск
- Том 55 / Номер 3
- Страницы
- 34-46
- Аннотация
По ряду частотных характеристик для набора переменных отдельно для регионов и городов России и стран Европы построены обобщенные главные компоненты для временного интервала 2011—2015 гг. в рамках метода STATIS. Использованы данные RLMS и EUROBAROMETER. Отбор критериев для анализа проведен в соответствии с процедурой оценивания связи между порядковыми переменными. Рассмотрены оценки уровня материального благосостояния, статуса респондентов, а также ряда критериев социальной напряженности (частота употребления алкоголя, закредитованность населения, оценка проблемы иммиграции, безработицы). Для этого были использованы полученные непосредственно от респондентов оценки. В рамках метода STATIS
удалось выявить группы взаимосвязанных показателей, формирующих максимальный вклад в компромиссное пространство. Компромиссное пространство строится по всем временным интервалам и всей совокупности рассматриваемых признаков. Предложены и апробированы способы вычисления элементов компромиссной (обобщенной) матрицы с учетом критерия максимальной информативности. Внутри компромиссного пространства определены группы населенных пунктов и стран. В качестве критериев разделения на группы использованы полученные в результате сингулярного разложения компромиссной матрицы элементы матрицы счетов. Научная новизна исследования состоит в применении метода обобщенных главных компонент для данных субъективного характера, имеющих вид порядковых переменных. Сопоставляются данные, полученные в ходе опросов населения регионов России и стран Европы.
- Ключевые слова
- качество жизни, удовлетворенность жизнью, многомерный статистический анализ, обобщенные главные компоненты, RLMS, EUROBAROMETER
- Дата публикации
- 22.08.2019
- Год выхода
- 2019
- Всего подписок
- 92
- Всего просмотров
- 2188
ВВЕДЕНИЕ
Большие объемы данных — явление, привычное для различных социально-экономических исследований. Однако число инструментов, позволяющих отслеживать динамику и выявлять слабые места в рядах наблюдений для фиксированного числа объектов в виде матриц размера  , ограничено.
, ограничено.
Особенное значение придается подобным методам в рамках исследования социально-экономических и социально-психологических категорий: «качество жизни» и «удовлетворенность жизнью» (Berenger, Verdier-Chouchane, 2007). Отметим, что основной характеристикой категории «Качество жизни» является отсутствие единого, общепризнанного ее определения, несмотря на большое число методологических концепций ее оценивания (Айвазян и др., 1989). Согласно определению, данному в (Айвазян и др., 1989), «качество жизни» — уникальная категория, являющаяся одновременно синтетической, объединяющей различные категории, сферы жизнедеятельности, и латентной, непосредственно измерить которую не представляется возможным. Однако если ставится задача субъективного определения качества жизни, то в некоторой степени возможна интеграция ряда оценок, полученных непосредственно от индивидов (Волкова, 2017).
В работе используется методология обобщенных главных компонент, инструментарий для оценивания которых был впервые предложен Бернардом Флури (Flury, 1986). Однако мы ориентируемся на несколько иную концепцию, а именно — на обобщение метода главных компонент для динамического ряда (Structuring Three-way Data Sets in Statistics, STATIS) (Escoufier, 1980; Lavit, 1988; Lavit et al., 1994; Abdi, Valentin, 2007). Метод позволяет сравнивать между собой наборы данных за разные интервалы времени, выявлять сходства и различия между отрезками времени, объектами наблюдения и выявлять те из них, которые в наибольшей степени формируют различные проблемы в структуре данных. Положим, исходные данные представляют собой таблицы значений p исходных признаков ( ) для i наблюдений (
) для i наблюдений ( ) по ряду лет
) по ряду лет  . К данным предъявляется требование: набор объектов — городов, регионов, стран, должен быть постоянен для всего исследуемого временного интервала. Мы предложили и апробировали варианты определения элементов компромиссной матрицы (ее определение будет дано далее):
. К данным предъявляется требование: набор объектов — городов, регионов, стран, должен быть постоянен для всего исследуемого временного интервала. Мы предложили и апробировали варианты определения элементов компромиссной матрицы (ее определение будет дано далее):
- выбор матрицы, соответствующей моменту времени t = 1 для отслеживания динамики относительно первой точки отсчета;
- определение компромиссной матрицы через усреднение имеющихся наборов данных по числу рассматриваемых временных интервалов;
- вычисление элементов компромиссной матрицы путем взвешивания значений исходных переменных в стандартизованном виде с помощью нормированных весовых коэффициентов. В качестве указанных коэффициентов выступают нормированные компоненты собственного вектора корреляционной матрицы (по временным отрезкам), соответствующего ее максимальному собственному значению.
Основной критерий выбора метода расчета элементов компромиссной матрицы — максимальная доля общей вариации исходных признаков, которую объясняет ее первая главная компонента.
ДАННЫЕ
Рассматриваются результаты опроса респондентов из 35 российских населенных пунктов (Приложение, п. 1) и 34 государств Европы за 2011—2015 гг. по базам RLMS и EUROBAROMETER; расчеты проводились в среде Matlab R2017.
В итоговый перечень переменных вошли те признаки, которые характеризуют качество работы, материального благосостояния, здоровья, оценки уровня закредитованности российских респондентов (Зубаревич, 2005). Также рассматривались комплексные критерии, позволяющие оценивать качество жизни в целом (Ратникова, Фурманов, 2014). Для случая европейских стран дополнительно рассматривались оценки миграционной активности, экономической ситуации, качества образования и здравоохранения в странах проживания респондентов (Johansson, 2002).
Перечень переменных был сформирован неслучайно. Признаки, отражающие отношение респондентов к какому-либо вопросу в обеих базах, — порядковые или бинарные переменные. По ним был проведен анализ таблиц сопряженности, а именно проверка взаимосвязи между рассматриваемыми порядковыми переменными с помощью γ-критерия Гудмана—Краскела (Goodman, Kruskal, 1954, 1959, 1963; Кендалл, Стьюарт, 1973).
Процедура расчета значений критерия основана на ранжировании откликов двух порядковых переменных (Bollen, Barb, 1981), — так с его помощью решается задача определения силы согласованности двух переменных (a, b), относящихся к одному набору объектов. В нашем случае таких наборов два: перечень населенных пунктов по выборке RLMS и набор стран по выборке EUROBAROMETER (O’Brien, 1979). Диапазон значений для γ меняется от –1 до +1. Причем при γ = –1 между переменными наблюдается полная обратная взаимосвязь, а при γ = +1 — полная прямая взаимосвязь. Если переменные независимы, то значение γ-критерия равно нулю (Гржибовский, 2008).
Основанием для включения переменных в список являлось попадание значения γ-критерия для пары переменных в один из двух интервалов:  или
или  , в соответствии со смысловой нагрузкой объясняющей переменной.
, в соответствии со смысловой нагрузкой объясняющей переменной.
Исходные данные — переменные с бинарным  или множественным откликом
или множественным откликом
где i — номер населенного пункта, r — номер респондента, l — номер вопроса с числом градаций k. Все исходные переменные были преобразованы в частотные характеристики:  .
.
Учитывались два нюанса. Во-первых, рассматривались только валидные частоты, т.е. отбрасывались пропущенные значения или пользовательские миссинги (отсутствие ответа на поставленный вопрос): «затрудняюсь ответить», «отказываюсь отвечать». Во-вторых, объектом исследования становились не респонденты, а населенные пункты, что достигалось за счет усреднения суммарного отклика для каждой градации по числу респондентов в конкретном населенном пункте (стране). Это было сделано с целью проведения динамического сопоставления в течение ряда лет. Рассматривались только некоторые градации из всех относящихся к конкретной переменной. Так, если у переменной — нечетное число градаций, то выделялись только те, которые находятся выше средней (их частоты суммировались). В случае если у переменной — две градации (1 и 0), то использовалась только градация «1». Опишем методику отбора на конкретных примерах из базы RLMS.
Пример 1. Переменная  . «Насколько вы удовлетворены своим материальным положением? Возможные градации: 1 — полностью удовлетворен»; 2 — в принципе удовлетворен; 3 — и да, и нет; 4 — не очень удовлетворен; 5 — совсем не удовлетворен».
. «Насколько вы удовлетворены своим материальным положением? Возможные градации: 1 — полностью удовлетворен»; 2 — в принципе удовлетворен; 3 — и да, и нет; 4 — не очень удовлетворен; 5 — совсем не удовлетворен».
Выделяя и суммируя частоты для первых двух градаций, мы имеем дело с теми респондентами, которые удовлетворены своим материальным положением.
Пример 2. Переменная  . «Есть ли у вашей семьи неоплаченные долги по кредитам? Возможные градации: 0 — нет; 1 — да».
. «Есть ли у вашей семьи неоплаченные долги по кредитам? Возможные градации: 0 — нет; 1 — да».
Для дальнейшего анализа этой переменной были использованы только частоты для ответа «1».
Разная смысловая нагрузка переменных обусловливает необходимость преобразования исходной статистической информации (была применена процедура стандартизации).
МЕТОДОЛОГИЯ
Опишем методологию STATIS в виде итеративной процедуры.
Итерация 1. Вычисление матричного произведения:  ,
,  , где
, где  — матрица стандартизованных значений для года t, t = 1,…, k (Rivadeneira et al., 2016), а
— матрица стандартизованных значений для года t, t = 1,…, k (Rivadeneira et al., 2016), а  — транспонированная матрица стандартизованных значений.
— транспонированная матрица стандартизованных значений.
Итерация 2. Определение скалярного произведения:  (Rivadeneira et al., 2016), где
(Rivadeneira et al., 2016), где  — произведение матриц стандартизованных значений за тот год
— произведение матриц стандартизованных значений за тот год  , который сопоставляется с текущим годом,
, который сопоставляется с текущим годом,  .
.
Итерация 3. Вычисление коэффициентов корреляции r:
(Rivadeneira et al., 2016). Матрица С  — корреляционная матрица, анализируя элементы которой можно определить пары лет, характеризующиеся бóльшим или меньшим (статистическим) сходством.
— корреляционная матрица, анализируя элементы которой можно определить пары лет, характеризующиеся бóльшим или меньшим (статистическим) сходством.
Итерация 4. Спектральное разложение корреляционной матрицы C:  , где
, где  . U — матрица, состоящая из собственных векторов матрицы С; U–1 — матрица, обратная ей, а V — диагональная матрица, на диагонали которой — собственные значения корреляционной матрицы С. Могут быть вычислены компоненты матрицы G (координаты каждого набора данных на плоскости главных компонент матрицы С):
. U — матрица, состоящая из собственных векторов матрицы С; U–1 — матрица, обратная ей, а V — диагональная матрица, на диагонали которой — собственные значения корреляционной матрицы С. Могут быть вычислены компоненты матрицы G (координаты каждого набора данных на плоскости главных компонент матрицы С):  (
( ) (Abdi, Valentin, 2007).
) (Abdi, Valentin, 2007).
Первый столбец матрицы U — собственный вектор, соответствующий максимальному собственному значению матрицы C. Тогда  — нормированные весовые коэффициенты.
— нормированные весовые коэффициенты.
Итерация 5. Определение элементов компромиссной (обобщенной) матрицы  (
( ), компоненты которой рассчитываются как линейная комбинация
), компоненты которой рассчитываются как линейная комбинация  объектов, взвешенных с помощью коэффициентов, рассчитанных на предыдущем шаге (Rivadeneira et al., 2016). Для случаев, если этот вариант построения дает невысокую информативность, нами были предложены иные методы. Среди них:
объектов, взвешенных с помощью коэффициентов, рассчитанных на предыдущем шаге (Rivadeneira et al., 2016). Для случаев, если этот вариант построения дает невысокую информативность, нами были предложены иные методы. Среди них:
- вычисление среднего значения по всем матрицам
 ,
, - выделение в качестве компромиссной матрицы одной из матриц
 и другие.
и другие.
Итерация 6. Спектральное разложение компромиссной матрицы:  (Rivadeneira et al., 2016). В результате определяются компоненты матрицы счетов и матрицы нагрузки.
(Rivadeneira et al., 2016). В результате определяются компоненты матрицы счетов и матрицы нагрузки.
Анализ данных RLMS
С помощью расчета значений γ-критерия Гудмана—Краскела был отобран ряд переменных (указан вместе с теми градациями, которые были использованы).
Перечень переменных (RLMS).
 : «Насколько вы удовлетворены своей работой в целом?» (уд_работой) —
: «Насколько вы удовлетворены своей работой в целом?» (уд_работой) —
k1 — полностью удовлетворен; k2 — в принципе удовлетворен.
 : «Насколько вы удовлетворены условиями своего труда?» (уд_усл_труда) —
: «Насколько вы удовлетворены условиями своего труда?» (уд_усл_труда) —
k1 — полностью удовлетворен; k2 — в принципе удовлетворен.
 : «Насколько вы удовлетворены своей заработной платой?» (уд_зарплатой) —
: «Насколько вы удовлетворены своей заработной платой?» (уд_зарплатой) —
k1 — полностью удовлетворен; k2 — в принципе удовлетворен.
 : «Насколько вы удовлетворены возможностями своего профессионального роста?» (проф_рост) —
: «Насколько вы удовлетворены возможностями своего профессионального роста?» (проф_рост) —
k1 — полностью удовлетворен; k2 — в принципе удовлетворен.
 : «Насколько вы удовлетворены своим материальным положением в настоящее время?» (уд_мат_положением) —
: «Насколько вы удовлетворены своим материальным положением в настоящее время?» (уд_мат_положением) —
k1 — полностью удовлетворен; k2 — в принципе удовлетворен.
 : «Представьте себе лестницу, где на первой ступени — богатые, а на девятой — нищие. На какой находитесь лично вы в настоящее время (изначально таких ступеней девять)?» (богатство) —
: «Представьте себе лестницу, где на первой ступени — богатые, а на девятой — нищие. На какой находитесь лично вы в настоящее время (изначально таких ступеней девять)?» (богатство) —
k1 — первая ступень (высшая); k2 — вторая ступень; k3 — третья ступень;
k4 — четвертая ступень.
 : «Представьте себе лестницу, где на первой ступени находятся те, кого больше всего уважают, а на девятой — те, кого совсем не уважают. На какой находитесь лично вы в настоящее время (изначально таких ступеней девять)?» (уважение) —
: «Представьте себе лестницу, где на первой ступени находятся те, кого больше всего уважают, а на девятой — те, кого совсем не уважают. На какой находитесь лично вы в настоящее время (изначально таких ступеней девять)?» (уважение) —
k1 — первая ступень (высшая); k2 — вторая ступень; k3 — третья ступень;
k4 — четвертая ступень.
 : «Как вы оцениваете свое здоровье в настоящее время?» (здоровье) —
: «Как вы оцениваете свое здоровье в настоящее время?» (здоровье) —
k1 — очень хорошее; k2 — хорошее.
 : «Курите ли вы в настоящее время?» (курение) —
: «Курите ли вы в настоящее время?» (курение) —
1 — да.
 : «Вы употребляете хотя бы иногда алкогольные напитки, включая пиво?» (алкоголь) —
: «Вы употребляете хотя бы иногда алкогольные напитки, включая пиво?» (алкоголь) —
1 — да.
 : «На сегодняшний день у вашей семьи есть какие-либо долги по кредитам?» (кредиты)
: «На сегодняшний день у вашей семьи есть какие-либо долги по кредитам?» (кредиты)
1 — да.
В табл. 1 приведена матрица C коэффициентов корреляции по российским данным.
Таблица 1. Матрица C коэффициентов корреляции (RLMS)
| Год | 2011 | 2012 | 2013 | 2014 | 2015 |
| 2011 | 1 | 0,71 | 0,60 | 0,60 | 0,38 |
| 2012 | 0,71 | 1 | 0,66 | 0,67 | 0,37 |
| 2013 | 0,60 | 0,66 | 1 | 0,63 | 0,38 |
| 2014 | 0,60 | 0,67 | 0,63 | 1 | 0,56 |
| 2015 | 0,38 | 0,37 | 0,38 | 0,56 | 1 |
Сходство между соседними интервалами логически объясняется их близостью на шкале времени. Тогда как значительный разрыв между начальной и конечной точкой — результат изменения субъективных оценок, обусловленных в том числе снижением уровня удовлетворенности респондентов материальным положением, работой. Причина такого снижения кроется в первую очередь в последствиях экономического кризиса 2014 г. В результате сингулярного разложения  матрицы С были определены ее собственные значения, находящиеся на диагонали матрицы V:
матрицы С были определены ее собственные значения, находящиеся на диагонали матрицы V:
 —
—
и собственные векторы — матрица U:
Определение компонент компромиссной матрицы в случае российских данных производилось двумя способами.
- Построение линейной комбинации
 ,
,  , где
, где  — нормированные компоненты собственного вектора корреляционной матрицы С, соответствующего ее максимальному собственному значению. Отсюда получаем
— нормированные компоненты собственного вектора корреляционной матрицы С, соответствующего ее максимальному собственному значению. Отсюда получаем  .
. - Усреднение исходных матриц по числу рассматриваемых K периодов времени:
 .
.
По результатам определения объясняющей силы двух компромиссных матриц для дальнейшего анализа был выбран второй вариант. В качестве иллюстрации полученных нами результатов приведем первые пять собственных значений матрицы. Соответствующие им пять первых главных компонент компромиссной матрицы вместе объясняют более 70% общей вариации признаков (табл. 2). Тогда как первый вариант определения элементов компромиссной матрицы дает меньшую информативность — пять первых главных компонент объясняют лишь 65% общей вариации.
Таблица 2. Собственные значения компромиссной матрицы (сегмент матрицы L) и доля общей вариации признаков (для семи первых главных компонент), вариант с выбором в качестве компромиссной матрицы среднего значения за 5 лет
| Собственное значение | Накопленная доля общей вариации признаков, % |
 | 28,9 |
 | 46,5 |
 | 57,5 |
 | 65,3 |
 | 72,5 |
| ... | … |
 | 100 |
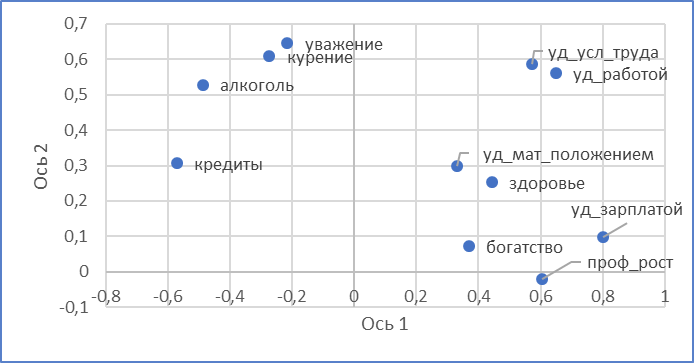
Для анализа структуры данных и проекции объектов на плоскость осей (главных компонент) компромиссной матрицы к ней, согласно итерационной процедуре, было проведено спектральное разложение  . По результатам спектрального разложения и дальнейшего анализа матрицы нагрузок определились группы признаков (максимально коррелированные друг с другом и с осями компромиссного пространства):
. По результатам спектрального разложения и дальнейшего анализа матрицы нагрузок определились группы признаков (максимально коррелированные друг с другом и с осями компромиссного пространства):
- - оценка материальной обеспеченности (причем уровень удовлетворенности материальным положением тесно связан с субъективной оценкой здоровья);
- - удовлетворенность работой и условиями труда;
- - наличие вредных привычек, статус в обществе (рис. 1).
Рис. 1. График нагрузок
Рассчитаны и построены проекции объектов (населенных пунктов) на плоскости первых двух главных компонент компромиссной матрицы (рис. 2) (Vermunt, Magidson, 2005). Для этого определены элементы матрицы счетов:  , размерностью
, размерностью  , где
, где  — матрица, состоящая из собственных векторов компромиссной матрицы, а
— матрица, состоящая из собственных векторов компромиссной матрицы, а  — диагональная матрица, на диагонали которой — собственные значения компромиссной матрицы, т.е.
— диагональная матрица, на диагонали которой — собственные значения компромиссной матрицы, т.е.  — квадратный корень матрицы
— квадратный корень матрицы  . Каждая строка матрицы
. Каждая строка матрицы  — объект наблюдения (населенный пункт), а каждый столбец — компонента компромиссного пространства.
— объект наблюдения (населенный пункт), а каждый столбец — компонента компромиссного пространства.

1 – Санкт-Петербург 2 – Москва 3 – Московская область 4 – Сыктывкар, Коми 5 – Волосовский район, Ленинградская область 6 – Смоленск 7 – Ржев, Тверская область 8 – Тула 9 – Куйбышевский район, Калужская область 10 – Нижний Новгород 11 – Шумерлинский район, республика Чувашия 12 – Земетченский район, Пензенская область 13 – Уварово, Тамбовская область 14 – Казань 15 – Саратов 16 – Вольск, Саратовская область 17 – Руднянский район, Волгоградская область 18 – Батайск, Ростовская область 19 – Краснодар 20 – Георгиевск, Ставропольский край 21 – Кущевский район, Краснодарский край 22 – Челябинск 23 – Курган 24 – Глазов, Удмуртия 25 – Орск, Оренбургская область 26 – Соликамск, Пермский край 27 – Красноармейск, Челябинская область 28 – Томск 29 – Сургутский район, Тюменская область 30 – Бийск, Алтайский край 31 – Курьинский район, Алтайский край 32 – Красноярск 33 – Владивосток 34 – Назарово, Красноярский край 35 – Тамбовский район, Амурская область
Произошло ожидаемое разделение всей совокупности объектов на группы. Так, в верхнем правом квадранте — наиболее благополучные объекты. Для них характерны высокие оценки материальной удовлетворенности, возможностей профессионального роста, условий труда. Помимо этого, здесь отмечается низкая степень кредитной задолженности, высокие оценки здоровья и статусные оценки (уважение со стороны окружающих).
Одни из наиболее отстающих — Вольск, Курьинский район (Алтайский край), Руднянский район (Волгоградская область). Здесь отмечаются низкие оценки труда и благосостояния, высокий уровень закредитованности населения (Якубов, 2009).
Для проверки устойчивости модели из анализа последовательно исключались исходные матрицы (всего было проведено пять вариантов исключения, начиная с 2011 г. и заканчивая 2015 г.). Эти процедуры не повлияли на результаты, информативность компромиссной матрицы не снижалась.
страны Европы
Для динамического анализа качества жизни в контексте субъективных оценок были отобраны 34 страны (Приложение, п. 2), среди которых есть как страны–члены ЕС, так и государства—кандидаты на вступление в ЕС)1.
Информационная база — стандартный EUROBAROMETER за 2011—2015 гг.2
Из всей совокупности переменных были отобраны девять признаков, имеющие максимальную связь с переменной «Удовлетворенность жизнью» (степень тесноты связи определялась путем расчета γ-критерия Гудмана—Краскела) (Dehley et al., 2002).
Преобразование переменных производилось по той же схеме, которая применялась для российских населенных пунктов.
Оценивались переменные (указаны рассматриваемые градации):
 : «Как вы оцениваете свою работу?» — k1: очень хорошо;
: «Как вы оцениваете свою работу?» — k1: очень хорошо; : «Как вы оцениваете финансовое положение семьи?» — k1: очень хорошо;
: «Как вы оцениваете финансовое положение семьи?» — k1: очень хорошо; : «Как вы оцениваете ситуацию в занятости в стране?» — k1: очень хорошо;
: «Как вы оцениваете ситуацию в занятости в стране?» — k1: очень хорошо; : «Вас беспокоит проблема инфляции?» — k1: да;
: «Вас беспокоит проблема инфляции?» — k1: да; : «Вас беспокоит проблема безработицы?» — k1: да;
: «Вас беспокоит проблема безработицы?» — k1: да; : «Вас беспокоит проблема иммиграции?» — k1: да;
: «Вас беспокоит проблема иммиграции?» — k1: да; : «Вас беспокоит состояние системы здравоохранения?» — k1: да;
: «Вас беспокоит состояние системы здравоохранения?» — k1: да; : «Вас беспокоит состояние системы образования?» — k1: да;
: «Вас беспокоит состояние системы образования?» — k1: да; : «Вас беспокоит состояние окружающей среды?» — k1: да.
: «Вас беспокоит состояние окружающей среды?» — k1: да.
В соответствии с методологией анализа матричнозначных временных рядов были рассчитаны компоненты матрицы  (для унифицированного изложения результатов оставлены те же обозначения, что и в предыдущем случае, но добавлен нижний индекс [EB] (сокращение от EUROBAROMETER). Компоненты корреляционной
(для унифицированного изложения результатов оставлены те же обозначения, что и в предыдущем случае, но добавлен нижний индекс [EB] (сокращение от EUROBAROMETER). Компоненты корреляционной  -матрицы
-матрицы 
(табл. 3). Здесь  для каждого периода
для каждого периода  , а также
, а также  для периода
для периода  ;
;  и
и  — исходная и транспонированная матрицы стандартизованных значений рассматриваемых признаков.
— исходная и транспонированная матрицы стандартизованных значений рассматриваемых признаков.
Таблица 3. Корреляционная матрица  (по данным EUROBAROMETER)
(по данным EUROBAROMETER)
| Год | 2011 | 2012 | 2013 | 2014 | 2015 |
| 2011 | 1 | 0,86 | 0,82 | 0,78 | 0,76 |
| 2012 | 0,86 | 1 | 0,93 | 0,90 | 0,81 |
| 2013 | 0,82 | 0,93 | 1 | 0,92 | 0,84 |
| 2014 | 0,78 | 0,90 | 0,92 | 1 | 0,91 |
| 2015 | 0,76 | 0,81 | 0,84 | 0,91 | 1 |
Сопоставив элементы матрицы С (по данным RLMS) и [[[image70]]][[[image70]]] (по данным EUROBAROMETER), мы отмечаем более сильную связь между отрезками времени во втором случае. Кроме того, определяется большее сходство между соседними отрезками. Минимальное значение коэффициента корреляции между 2011 и 2015 г. — с течением времени между ними произошло некоторое число преобразований, самое заметное из которых — изменение отношения респондентов к иммиграции. Особенно это касается тех стран, куда были направлены наибольшие миграционные потоки из регионов Северной Африки и Ближнего Востока, — Германия, Италия, Швеция (Суворова, 2018).
Определены собственные значения матрицы [[[image70]]][[[image70]]]:
Учитывая разницу между первым и вторым собственными значениями матрицы [[[image70]]][[[image70]]], можно ожидать большей информативности компромиссного пространства, построенного по европейским данным. Матрица собственных векторов корреляционной матрицы [[[image70]]][[[image70]]] имеет вид:
Исходя из значений полученных нормированных весовых коэффициентов  , наименьший вклад в компромиссное пространство имеют матрицы за 2011—2015 гг. Компоненты компромиссной матрицы для европейских стран определены в виде
, наименьший вклад в компромиссное пространство имеют матрицы за 2011—2015 гг. Компоненты компромиссной матрицы для европейских стран определены в виде  , поскольку первая главная компонента компромиссной матрицы объясняет в этом случае 59% общей вариации признаков.
, поскольку первая главная компонента компромиссной матрицы объясняет в этом случае 59% общей вариации признаков.
Построена проекция 34 объектов (стран) на плоскость первых двух главных компонент компромиссной матрицы (рис. 3).
Рис. 3. Проекция стран на оси (1; 2) компромиссного пространства Верстка! Названия полностью или заменить на цифры. Расшифровка:
1 – Франция 2 – Бельгия 3 – Голландия 4 – Германия (Запад) 5 – Италия 6 – Люксембург 7 – Дания 8 – Ирландия 9 – Великобритания 10 – Северная Ирландия 11 – Греция 12 – Испания 13 – Португалия 14 – Германия (Восток) 15 – Финляндия 16 – Швеция 17 – Австрия 18 – Кипр 19 – Чехия 20 – Эстония 21 – Венгрия 22 – Латвия 23 – Литва 24 – Мальта 25 – Польша 26 – Словакия 27 – Словения 28 – Болгария 29 – Румыния 30 – Турция 31 – Хорватия 32 – Кипр (Турецкая часть) 33 – Македония 34 – Черногория
Вся совокупность стран очень четко разделилась на группы. С одной стороны, богатые страны с развитой экономикой, население которых, по большей части, довольно своим материальным положением, работой, высоко оценивает состояние систем образования и здравоохранения, а также выражает обеспокоенность миграционными процессами. С другой — страны юга и центра Европы. Особенно выделяются Испания, Кипр, Хорватия, Португалия, Греция (точка с номером 11 на рис. 3). Для них характерны высокий уровень безработицы, невысокая (субъективная) материальная обеспеченность домашних хозяйств и множество других, сопряженных с перечисленными, проблем. Последовательное исключение исходных матриц из анализа не нарушило устойчивости модели.
Заключение
Для анализа матричнозначных временных рядов на диапазоне 2011—2015 гг. к данным субъективного характера был применен ряд матричных преобразований в рамках метода STATIS. Определена теснота связи между рассматриваемыми временными отрезками для обоих случаев. Для российских данных коэффициенты корреляции между матрицами объект-признак по российским данным ниже, чем в случае анализа стран Европы. Это в первую очередь обусловлено более значимыми изменениями в оценках, полученных от респондентов, проживающих в Российской Федерации. Компромиссные (обобщенные) матрицы получены для двух совокупностей исходных данных. В обоих случаях отмечена устойчивость полученных результатов. Определены группы объектов, расположенных максимально близко относительно друг друга на плоскости первых двух главных компонент обобщенных матриц. Разделение европейских стран на группы более иллюстративно: четко отделены друг от друга группы благополучных и неблагополучных стран. В список самых благополучных попали две страны: Дания и Швеция. Москва, Московская область и город Сургут — тройка лидеров по субъективному качеству жизни среди российских населенных пунктов.
Приложение
1. Перечень населенных пунктов и переменных, вошедших в анализ удовлетворенности жизнью населения (по данным RLMS):
1) Санкт-Петербург; 2) Москва; 3) Московская область; 4) Сыктывкар, Коми; 5) Волосовский район, Ленинградская область; 6) Смоленск; 7) Ржев, Тверская область; 8) Тула; 9) Куйбышевский район, Калужская область; 10) Нижний Новгород; 11) Шумерлинский район, Республика Чувашия; 12) Земетченский район, Пензенская область; 13) Уварово, Тамбовская область; 14) Казань; 15) Саратов; 16) Вольск, Саратовская область; 17) Руднянский район, Волгоградская область; 18) Батайск, Ростовская область; 19) Краснодар; 20) Георгиевск, Ставропольский край; 21) Кущевский район, Краснодарский край; 22) Челябинск; 23) Курган; 24) Глазов, Удмуртия; 25) Орск, Оренбургская область; 26) Соликамск, Пермский край; 27) Красноармейск, Челябинская область; 28) Томск; 29) Сургутский район, Тюменская область; 30) Бийск, Алтайский край; 31) Курьинский район, Алтайский край; 32) Красноярск; 33) Владивосток; 34) Назарово, Красноярский край; 35) Тамбовский район, Амурская область.
2. Перечень населенных пунктов и переменных, вошедших в анализ удовлетворенности жизнью населения (по данным Eurobarometer):
1) Франция; 2) Бельгия; 3) Голландия; 4) Германия (Запад); 5) Германия (Восток) (комментарий: в таком виде, с учетом территориального разделения, приводится информация в системе EUROBAROMETER, поскольку прежде ФРГ и ГДР приписывались разные весовые коэффициенты, которые сейчас не используются); 6) Люксембург; 7) Дания; 8) Ирландия; 9) Великобритания; 10) Северная Ирландия; 11) Греция; 12) Испания; 13) Португалия; 14) Италия; 15) Финляндия; 16) Швеция; 17) Австрия; 18) Кипр; 19) Чехия; 20) Эстония; 21) Венгрия; 22) Латвия; 23) Литва; 24) Мальта; 25) Польша; 26) Словакия; 27) Словения; 28) Болгария; 29) Румыния; 30) Турция; 31) Хорватия; 32) Кипр (Турецкая часть); 33) Македония; 34) Черногория.
Библиография
- 1. Айвазян С.А., Бухштабер В.М., Енюков И.С., Мешалкин Л.Д. (1989). Прикладная статистика: Классификация и снижение размерности. Айвазян С.А. (общ. ред.). М.: Финансы и статистика.
- 2. Волкова М.И. (2017). Выявление факторов удовлетворенности жизнью в России и Европе // Социальная политика и социология. № 5. С. 6—15.
- 3. Гржибовский А.М. (2008). Анализ порядковых // Экология человека. № 8. С. 56—62.
- 4. Зубаревич Н.В. (2005). Россия регионов: в каком социальном пространстве мы живем? Независимый институт социальной политики. М.: Поматур.
- 5. Кендалл М., Стьюарт А. (1973). Статистические выводы и связи. Т. 2. Колмогорова А.Н. (общ. ред.). М.: Наука, Физматлит.
- 6. Ратникова Т.А., Фурманов К.К. (2014). Анализ панельных данных и данных о длительности состояний. Учебное пособие. НИУ ВШЭ. М.: Изд. дом Высшей школы экономики.
- 7. Суворова В.А. (2018). Миграционный кризис в Европе: проблемы вынужденной миграции // Власть. № 1. P. 176—179.
- 8. Якубов А.Х. (2009). Цели, критерии и методические подходы к оптимизации сельских поселений в муниципальном районе // Вестник Челябинского государственного университета. № 26 (164). С. 104—109.
- 9. Abdi H., Valentin D. (2007). Multiple Correspondence Analysis. In: Salkind N. (ed.) “Encyclopedia of Measurement and Statistics”. Thousand Oaks: Sage. P. 652—658.
- 10. Berenger V., Verdier-Chouchane A. (2007). Multidimensional Measures of Well-Being: Standard of Living and Quality of Life Across Countries // World Development. Vol. 35. No. 7. P. 1259—1276.
- 11. Flury B.N. (1986). Asymptotic Theory for Common Principal Component Analysis // The Annals of Statistics. Vol. 14. No. 2. P. 418—430.
- 12. Bollen K.A., Barb K.H. (1981). Pearson’s r and Coarsely Categorized Measures // American Sociological Review. Vol. 46. Р. 232—239. https://doi.org/10.2307/2094981.
- 13. Dehley J., Bpehnke P., Habich R., Zapf W. (2002). Quality of Life in a European Perspective: The Euromodule as a New Instrument for Comparative Welfare Research // Social Indicators Research. Vol. 58. P. 163—176.
- 14. Escoufier Y. (1980). L’analyse conjointe de plusieurs matrices de donnees. In: Jolivet M. (ed.) “Biometrie et Temps. Paris: Societe Francaise de Biometrie”. P. 59—76. [Электронный ресурс] Режим доступа: https://www.gesis.org/fileadmin/upload/dienstleistung/daten/umfragedaten/eurobarometer/eb_bibliography/EB_Bibliography.pdf, свободный. Загл. с экрана. Яз. фран. (дата обращения: декабрь 2018 г.).
- 15. Goodman L., Kruskal W.H. (1954). Measures of Association for Crossclassification I // Journal of the American Statistical Association. Vol. 49. Р. 732—764.
- 16. Goodman L., Kruskal W.H. (1959). Measures of Association for Crossclassification II // Journal of the American Statistical Association. Vol. 54. P. 123—163.
- 17. Goodman L., Kruskal W.H. (1963). Measures of Association for Crossclassification III // Journal of the American Statistical Association. Vol. 58, pp. 310 – 364.
- 18. Johansson S. (2002). Conceptualizing and Measuring Quality of Life for National Policy // Social Indicators Research. Vol. 58. P. 13—32.
- 19. Lavit C. (1988). Analyse conjointe de tableaux quantitatifs. Paris: Masson.
- 20. Lavit C., Escoufier Y., Sabatier R., Traissac P. (1994). The ACT (STATIS method) // Computational Statistics & Data Analysis. Vol. 18. P. 97—119.
- 21. O’Brien R.M. (1979). The Use of Pearson’s with Ordinal Data // American Sociological Review. Vol. 44. Р. 851—857. https://doi.org/10.2307/2094532.
- 22. Rivadeneira F.J., Figueiredo A.M.S., Figueiredo F.O.S., Carvajal S.M., Rivadeneira R.A. (2016). Analysis of Well-being in OECD Countries Through STATIS Methodology // HOLOS. Vol. 7. P. 335—351.
- 23. Vermunt J.K., Magidson J. (2005). Factor Analysis with Categorical Indicators: A Comparison between Traditional and Latent Class Approaches. In: Quantitative methodology series. New Developments in Categorial Data Analysis for the Social and Behavioral Sciences. Ark L.A. van der, Croon M.A., Sijtsma K. (eds). Mahwah: Lawrence Erlbaum Associates Publishers. P. 41—62.