Везде
К теории кредита и процентной ставки
Оглавление
Аннотация Оценить Содержание публикации
Библиография Комментарии
Поделиться
QR
Метрика
К теории кредита и процентной ставки
Аннотация
Код статьи
S042473880014718-8-1
DOI
10.31857/S042473880014718-8
Тип публикации
Статья
Статус публикации
Опубликовано
Авторы
Некипелов Александр Дмитриевич 
Должность: директор
Аффилиация: Московская школа экономики МГУ им. М.В.Ломоносова
Адрес: Москва, ул. Косыгина, д. 2 к. 1, кв. 9
Выпуск
Том 57 Номер 2
Страницы
5-20
Аннотация

С учетом особенностей методологии чистой экономической теории в статье исследуются корневые предпосылки возникновения кредитных отношений. В качестве объекта анализа избрана модель простой меновой экономики, причем при абстрагировании от явлений и процессов, происходящих вне сферы обращения. Показаны уязвимые пункты двух имеющихся подходов к анализу общей природы кредита: на основе объединения в единой функции полезности текущих и будущих благ и допущения о наличии у потребителей временно́го предпочтения. При принятых ограничениях достаточным условием для возникновения кредитных отношений оказывается существование благ, порождающих поток потребительских услуг (капитальных потребительских благ), а не единовременное удовлетворение потребностей. В ходе решения поставленной задачи обнаруживается неразрывная связь между текущим и трансвременным обменом, выявляется единая основа у потребительского и производственного кредитов, связанная с их использованием винвестиционных целях. Становится ясным, что отношения кредита логически предшествуют деньгам, а не наоборот, как это часто предполагается при их анализе.

Ключевые слова
чистая экономическая теория, простая меновая экономика, кредитные отношения, чистая торговля и чистый кредит, производственный кредит, потребительский кредит, процентная ставка, функции и функционалы трансвременной полезности, временное предпочтение, капитальные потребительские блага.
Классификатор
Получено
16.06.2021
Дата публикации
25.06.2021
Всего подписок
18
Всего просмотров
1370
Оценка читателей
0.0 (0 голосов)
Цитировать   Скачать pdf
1

1. Постановка проблемы и общая теория кредита
2 1.1. Постановка проблемы
3 С точки зрения отстаиваемой нами методологии чистой экономической теории (Некипелов, 2006, 2017, 2019а) принципиальное значение имеет вопрос о том, на какой стадии исследования возникает возможность вводить в анализ те или иные экономические явления. Ответ на него призван выявить условия, минимально необходимые для формирования соответствующих экономических отношений, и дать на этой основе исходную, наиболее абстрактную характеристику их природы. В ходе последующего анализа эти сведения должны обогащаться и конкретизироваться, что, как предполагается, позволит в конечном счете получить целостное представление об исследуемой экономической системе.
4 Эти соображения важны для понимания проблемы, которой посвящена настоящая статья. Мы попробуем показать, что условия для появления отношений заимствования (кредита) могут (а потому и должны, с точки зрения упомянутой выше методологии) быть выявлены в рамках модели простой меновой экономики.
5 Меновая экономика представляет собой как бы вторую (после модели «робинзонады» (Некипелов, 2019б)) ступеньку, на которой предметом исследования становится взаимодействие экономических агентов, являющихся собственниками производимой ими продукции. Именно на этом уровне анализа появляется возможность выявить природу важнейших для рыночной системы отношений — отношений обмена (пока — натурального), а также обнаружить силы, которые приводят к развитию общественного разделения труда.
6 Экономическая теория давно установила тот факт, что отношения обычного (текущего) обмена уходят корнями в особенности индивидуальных предпочтений и потому могут быть введены в анализ при абстрагировании от сферы производства. Из анализа модели чистой торговли следует, что необходимым условием взаимовыгодного обмена является несовпадение предельных оценок двух благ у его потенциальных участников. Естественно, возникает вопрос, а как обстоит дело с трансвременным обменом, реализующимся через отношения заимствования. Можем ли мы и здесь говорить о чистом кредите, т.е. о таком кредите, предпосылки которого складываются в сфере обращения, или для этих целей необходимо выйти за ее рамки? И если нам все же удастся найти основания для того, чтобы вводить в рассмотрение кредитные отношения без обращения к сфере производства, будут ли они в полной мере симметричны тем, которые определяют аналогичную возможность для обычных (текущих) меновых отношений?
7 Таков комплекс вопросов, являющихся предметом настоящей статьи.
8 1.2. Имеющиеся наработки по общей теории кредита
9 Изложенный выше методологический подход не является общепринятым. В рамках господствующей эмпирической науки экономическая теория рассматривается как совокупность моделей, каждая из которых опирается на определенные гипотезы и некоторый комплекс наблюдаемых явлений и на их основе формулирует экономические закономерности, подлежащие практической верификации. При этом неизбежным оказывается использование в моделях категорий, отражающих экономические явления, природа которых не была ранее определена. Соответственно, не придается значения и вопросу о том, каковы минимальные условия, необходимые для включения в анализ того или иного явления.
10 Эти особенности эмпирической науки проявляются и в трактовке природы кредита. Так, в учебниках, претендующих на систематическое изложение предмета, проблематика отношений заимствования возникает, как правило, далеко не в первых главах1, причем после того как введено понятие «экономические издержки» (между тем, последние, как известно, включают процент на применяемый капитал). Кроме того, в подавляющем большинстве случаев отношения кредита рассматриваются сторонниками эмпирической теории применительно к условиям денежной экономики. В этом случае объектом этих отношений являются деньги, а процентная ставка выступает в качестве цены денег, т.е. той добавочной суммы, которую заемщик должен отдать кредитору в установленный соглашением срок.
1. К примеру, в учебнике (Mas-Colell, Whinston, Green, 1995) кредит становится объектом рассмотрения лишь в главе 20, в учебнике (Katzner, 2006) — в главе 13, в учебнике (Silberberg, 1990) — в главе 12.
11 Сказанное не означает, что в ходе изучения отношений заимствования, ведущегося уже не одно столетие, не было получено значимых результатов о причинах возникновения трансвременного обмена и данный вопрос мог остаться вне поля зрения исследователей. Другое дело, что получение ответа на него не рассматривалось как составная часть усилий, направленных на построение упорядоченного интеллектуального макета рыночной экономической системы.
12 Весьма распространена — и, на наш взгляд, вполне справедливо — точка зрения, в соответствии с которой основное направление исследований в этой области было задано еще Е. Бем-Баверком (Böhm-Bawerk, 1890), сформулировавшим три возможных причины существования кредита:
13 1) экономический рост и связанные с этим ожидания повышения уровня благосостояния (способствует повышению благосостояния благодаря выравниванию уровня потребления); 2) предпочтение текущего потребления по отношению к будущему; 3) использование окольных методов производства.
14 Первая из указанных причин дала импульс развитию исследований, направленных на выяснение того, каким образом кредит способен содействовать выравниванию уровней потребления на различных этапах жизни людей, и породила особый класс моделей, в которых взаимодействуют так называемые перекрывающиеся поколения. Ключевую роль в развитии этих исследований сыграли труды М. Алле и П. Самуэльсона (Allais, 1947; Samuelson, 1958).
15 Третья причина породила многочисленные разработки в области экономической динамики и определения оптимального уровня накопления. Среди них можно отметить работы (Malinvaud, 1953; Swan, 1956; Solow, 1956; Weizsacker, 1971; Gale, 1973; Bliss, 1975).
16 Однако эти, несомненно, важные исследования находятся за рамками сформулированной нами задачи. С точки зрения методологии чистой экономической теории к этим вопросам следовало бы обратиться на более поздних этапах формирования интеллектуального макета экономической системы. По этой же причине не имеют прямого отношения к нашей теме и публикации по проблемам связи между деньгами и кредитом, среди которых важное место занимает известная работа Л. фон Мизеса «Теория денег и кредита», написанная в 1912 г. (Mises, 1971).
17 Поэтому здесь нас должны интересовать результаты, полученные прежде всего в ходе исследований, направленных на увязку кредитных отношений с особенностями индивидуальных предпочтений (вторая причина — по Е. Бем-Баверку). Их немало. Прежде всего следует отметить выявление двух возможных подходов к учету фактора времени при анализе индивидуальных предпочтений.
18 Первый подход основан на применении отношений предпочтения не только к различным благам, но и к одним и тем же благам, получаемым потребителем в различные моменты (периоды) времени. В этом случае величина трансвременной полезности оказывается простой функцией, аргументами которой являются уровни потребления всех благ (или агрегированные уровни потребления) во все рассматриваемые моменты времени.
19 Суть второго подхода состоит во введении особых отношений предпочтения между уровнями благосостояния, реализуемыми индивидуумом в различные моменты времени. В этом случае величина трансвременной полезности оказывается функционалом, аргументами которого являются функции полезности, относящиеся к отдельным моментам времени.
20 Несложно убедиться, что первый подход позволяет рассматривать натуральные кредитные отношения как обычный обмен двух благ. В самом деле, пусть функция полезности потребителя имеет вид
21
U=Ux1t,…,xnt , (1)
22 где i=1,…,n — виды потребляемых благ, t=1,…,T — моменты (периоды) потребления. Тогда, если предельная норма замещения блага i 1 в период t благом i , но t+1 -периода (т.е. ∂x1t+1/∂x1t ) одного потребителя будет отличаться от аналогичного показателя другого потребителя, то возникают условия для взаимовыгодного обмена между ними. И, как известно, согласно теории чистой торговли пропорция обмена должна находиться в промежутке между относительными предельными оценками блага i у участников обмена. Но разность количества блага x1t и блага x1t+1 , являющаяся результатом применения одной из таких пропорций обмена, может рассматриваться и как выраженный в натуральной форме процент от сделки предоставления этого блага в кредит одним участником другому. А это значит, что при таком подходе полностью исчезает различие между обычным и трансвременным обменами, между пропорцией обмена и процентной ставкой. Более того, оказывается, что по одним товарам кредитором может быть один контрагент, а по другим — другой.
23 Поскольку проблематика кредитных отношений в подавляющем большинстве случаев рассматривается сторонниками эмпирической теории применительно к условиям денежной экономики, то появляется возможность представить сопутствующее кредиту перераспределение экономическим агентом потребления во времени в удобном скалярном виде — через изменения размера находящегося в его распоряжении денежного дохода. Еще И. Фишер в обоснование этого приема ссылался на то, что доход, в сущности, является синонимом потребления: в случае, когда владелец денег воздерживается от его немедленного расходования, происходит всего лишь перераспределение потребления во времени (Fisher, 1970)2.
2. Первое издание книги И. Фишера относится к 1930 г.
24 Замена в функции полезности (1) отдельных благ, потребляемых в разные периоды, агрегированным уровнем потребления, или доходом разных периодов (см., например, (Silberberg, 1990)), приводит к необходимости внести небольшое уточнение в представленные выше выводы. Пусть функция полезности имеет вид
25 U=Uyt, (2)
26 где yt — уровни дохода в периоды 1,…,T.
27 Допустим, что yt0 — вектор дохода, которым потребитель будет заведомо располагать в периоды 1,…,T (эти величины могут быть, а могут и не быть равными друг другу). Если через r обозначить процентную ставку, используя которую потребитель может перераспределять имеющийся у него доход во времени, то 1+rt-1 будет представлять альтернативные издержки потребления единицы дохода в текущий период, оцененные через утраченную полезность периода t . Соответственно, 1/1+rt-1 является выражением альтернативных издержек потребления единицы дохода в период t , измеренных через утраченную полезность текущего (первого) периода. Тогда текущую величину богатства можно определить как приведенную ценность текущего и будущего дохода W=∑t=1Tyt/1-rt-1 . В результате кредитных отношений эта величина богатства W не может измениться (она может только перераспределиться во времени). Поэтому
28 ∑t=1Tyt0/1-rt-1=∑t=1Tyt/1-rt-1=W,
29 или
30 ∑t=1Tyt0-yt/1-rt-1=0. (3)
31 Максимизация целевой функции (2) при соблюдении ограничения, заданного уравнением (3), требует соблюдения следующих необходимых условий (соблюдение достаточных условий максимума гарантируется квазивогнутостью и возрастающим характером функции полезности (2)):
32 It=∂U∂y1-λ1-rt-1=0, t=1,…,T, (4)
33 Iλ=∑t=1Tyt0-yt/1-rt-1=0, (5)
34 где It и Iλ — частные производные функции Лагранжа, построенной на основе целевой функции (2) и ограничения (3).
35 Система уравнений (4)–(5) может быть решена относительно yt . В результате получаем маршаллианские функции спроса на потребление (доход) в периоде t : yt=ytr,yt0.
36 Если взять два уравнения It ( t=t и t=t+1 ) и разделить их друг на друга, получим важное выражение
37 ∂U∂yt/∂U∂yt+1=∂yt+1∂yt=1+r.
38 Оно свидетельствует о том, что в оптимальном положении абсолютная величина предельной нормы замещения дохода периода t доходом периода t+1 должна равняться единице плюс процентная ставка, т.е. альтернативной оценке дохода первого периода.
39 Отсюда следует, что если предельная норма замещения потребления периода t потреблением периода t+1 больше 1+r , то потребителю выгодно привлекать кредит, в противоположном же случае — невыгодно. Очевидным становится и механизм формирования равновесной процентной ставки: она будет установлена рынком на таком уровне, на котором спрос на кредит и его предложение уравновесят друг друга.
40 Как и в рассмотренном выше случае, мы имеем в этом отношении полную аналогию с текущим обменом. Но в отличие от модели, в которой в качестве аргументов функции (трансвременной) полезности используются все блага, потребляемые во все периоды времени, здесь исключена ситуация, когда во взаимоотношениях двух экономических агентов каждый может выступать и в качестве кредитора, и в качестве заемщика.
41 Как отмечалось выше, изложенный подход к определению условий формирования кредитных отношений в увязке исключительно с особенностями индивидуальных предпочтений потребителей не является единственным. Дело в том, что его применение сопряжено со своеобразным умалением роли фактора времени, которое оказывается не более чем одной из характеристик благ (уровней потребления, дохода). Это ограничение снимает подход, основанный на введении особых отношений предпочтения между уровнями благосостояния, реализуемыми индивидуумом в различные моменты (периоды) времени (см., в частности, (Silberberg, 1990, p. 419–420; Mas-Colell, Whinston, Green, 1995, p. 732)). В данном случае трансвременная функция (функционал) полезности принимает вид
42 V=VU1,…,UT, (6)
43 где V — трансвременная функция полезности, U1,…,UT — текущие уровни полезности в периоды 1,…,T .
44 Использование трансвременного функционала полезности (6) предполагает определенную конкретизацию его свойств, относящихся к характеру зависимости величины трансвременной полезности V от текущих полезностей U1,…,UT .
45 В середине 1950-х годов Р. Стротц обратил внимание на необходимость того, чтобы трансвременные функции полезности были динамически консистентными (состоятельными). Это означает, что сравнительная величина (предельная норма замещения) полезностей двух периодов должна оставаться неизменной при ее оценке, опирающейся на разные точки отсчета (Strotz, 1956, p. 165–180). Необходимость наложения соответствующих ограничений на структуру функции (6) была фактически безоговорочно принята экономическим сообществом.
46 Более сложной оказалась судьба гипотезы о наличии у потребителей временно́го предпочтения, которая была сформулирована еще Е. Бем-Баверком и подробно разработана И. Фишером (Fisher, 1970). Воплощение этой гипотезы возможно различными способами3, но наиболее распространенной стала аддитивная функция вида:
3. В частности, Т. Купманс привлек внимание (Koopmans, 1960) к широкому классу рекуррентных функций полезности, частным случаем которых является и функция (7). Все функции этого семейства предполагают наличие временно́го предпочтения, хотя показатель нетерпения ρ может быть не постоянной, а переменной величиной.
47 VU1,…,UT=∑t=1TUtyt1+ρt-1,     ρ≥0, (7)
48 где yt — уровень потребления экономического агента в период t , ρ≥0 — показатель, определяющий степень его нетерпения. При этом важно, что функция (7) является динамически состоятельной по Стротцу: предельная норма замещения полезностью любого следующего периода полезности периода предыдущего всегда равняется одной и той же величине -1+ρ.
49 Наличие временно́го предпочтения ведет к возможности потребителя получить эффект от участия в кредитных отношениях. Для этого, ради простоты, рассмотрим механизм максимизации трансвременной полезности V на отрезке времени, состоящем из двух периодов, и при предположении, что в начальный момент каждого периода потребитель обладает одинаковым количеством благ, обеспечивающих уровень потребления e . В этих условиях модель максимизации трансвременной полезности будет иметь вид
50 VU1,U2=U1y1+U2y2/1+ρ
51 при условиях y1=e+crdt, y2=e-crdt1+r, где crdt — размер кредита, привлеченного («+») / предоставленного («–») потребителем; r — уровень процентной ставки.
52 Техника, связанная с использованием функции Лагранжа, позволяет убедиться в том, что, во-первых, размер кредита (привлекаемого или предоставляемого) является функцией процентной ставки (т.е.  crdt=crdtr ), а во-вторых, что максимум трансвременной полезности будет достигаться при таком размере кредита, при котором соблюдается равенство
53 ∂y1/∂y2=-1+r/1+ρ. (8)
54 Следовательно, когда процентная ставка выше показателя нетерпения, потребителю будет выгодно предоставлять кредит, и наоборот — он будет привлекать кредит в ситуации, когда ρ>r.
55 Поскольку условие (8) относится к любому потребителю, несложно сделать вывод, что необходимым условием формирования кредитных отношений является исходное неравенство у двух индивидуумов предельных норм замещения текущего потребления будущим4. Соответственно, равновесной будет такая величина процентной ставки, при которой суммарные спрос на кредит и его предложение будут совпадать друг с другом.
4. Следует иметь в виду, что неравенство у потребителей предельных норм замещения текущим доходом (потреблением) будущего (т.е. ∂y1/∂y2 ) не противоречит требованию состоятельности функционала трансвременной полезности, которое предполагает равенство минус единице предельной нормы замещения текущей полезностью будущей (т.е. ∂Ut/∂Ut+1 ).
56 Эти выводы очевидным образом коррелируют с теми, которые вытекают из рассмотренной выше модели с простой функцией трансвременной полезности (см. уравнения (2)–(5)) и, соответственно, с условиями текущего обмена: во всех случаях условием взаимовыгодности сделок (и трансвременных, и текущих) является неравенство предельных оценок объектов обмена потребителями. Преимущество модели с трансвременным функционалом полезности состоит в том, что в ней не происходит размывания различия между текущим и трансвременным обменами, а, следовательно, — и различия между пропорциями обычного обмена и процентной ставкой5.
5. Последнее можно наглядно продемонстрировать, если усложнить модель, представив функции текущей полезности как Utx1t,…,xnt , где xit — количество потребляемых благ i в период t , и введя ограничения, обеспечивающие неизменность совокупной меновой ценности благ в процессе текущего обмена. Этот прием будет использован нами при анализе модели, не предусматривающей наличия временно́го предпочтения у потребителей.
57 Несмотря на эти достоинства, подход, основанный на гипотезе временно́го предпочтения, в течение длительного времени остается объектом острой дискуссии. Оппоненты ссылаются на то, что признание предпочтительности благ текущих перед благами будущими равносильно утверждению о близорукости людей6. Ф. Рамсей еще в 1920-е годы связывал нетерпеливость потребителя со слабым воображением (Ramsey, 1928).
6. Характерно следующее высказывание Ю. Сильберберга: «…Существование временно́го предпочтения является сомнительным и эмпирически неподтвержденным. Оно предполагает наличие близорукости в отношении времени. Если мы знаем, что будущее придет (а неопределенность будущего не рассматривается как источник временно́го предпочтения), почему будущее должно оцениваться ниже, чем настоящее? Переместив потребление на более близкий срок, не пожалеем ли мы об этом, когда будущее настанет, и разве мы не могли заранее предвидеть это сожаление?» (Silberberg, 1990, p. 420).
58 Есть свои аргументы и у сторонников гипотезы временно́го предпочтения. Согласно одному из них дисконт 1/1+ρ может рассматриваться и как вероятность дожития до следующего периода (Mas-Colell, Whinston, Green, 1995, p.734), и как отражение роли полезности будущих поколений для полезности текущего поколения (Barro, 1989)7.
7. С точки зрения применяемой нами методологии эти аргументы не работают, поскольку в той простейшей модели, которая является объектом исследования, потребитель лишен и возраста, и пола, и семейного положения. Все эти факторы должны быть приняты во внимание на более поздних этапах анализа.
59 С учетом сказанного, мы можем конкретизировать сформулированную в начале статьи постановку интересующего нас вопроса. Не отвергая заведомо принципиальную возможность существования у ряда или даже у всех потребителей временно́го предпочтения, попытаемся выяснить, исключает ли отказ от этой гипотезы всякую возможность объяснения чистых кредитных отношений на стадии анализа простой меновой экономики.
60

2. О возможности чистого кредита при отсутствии у потребителей временного предпочтения
61 2.1. Случай обычных благ
62 Интересующую нас проблему мы будем рассматривать в дискретном времени. Такой подход представляется вполне оправданным — он отвечает реальному поведению людей, которые делят непрерывное время своей жизни на отдельные отрезки времени и с учетом этого принимают решения.
63 Функционал трансвременной полезности, наряду с обычными свойствами — возрастающим характером, квазивогнутостью (следовательно, и убывающей предельной нормой замещения полезности текущей полезностью будущей) и динамической состоятельностью — будет характеризоваться также отсутствием временно́го предпочтения (т.е. ∂Ut+1y0/∂Uty0=-1 )8.
8. Такими свойствами обладают, например, функции типа V=∑tUtα.
64 С учетом отсутствия в нашей модели денег возможны два способа решения вопроса об аргументах функций текущей полезности.
65 Первый состоит в использовании конструкции композитного блага, представляющего набор, в который входят все блага с фиксированными долями. С математической точки зрения этот подход ничем не отличается от подхода, когда в качестве аргумента функций текущей полезности выступает денежный доход потребителя. Этот подход представляется не самым удачным по трем причинам. Во-первых, выражение динамики потребления через композитное благо сопряжено с серьезными натяжками: в большинстве случаев изменение потребления различных благ происходит неравномерно. Во-вторых, агрегирование потребительских благ исключает возможность анализа связи между чистой торговлей и чистым кредитом. В-третьих, композитное благо (как и доход) лишает нас возможности учитывать специфику удовлетворения потребностей различными видами благ. Значимость этого обстоятельства станет ясна позднее.
66 В силу сказанного мы будем опираться на второй способ решения проблемы — использование в качестве независимых переменных текущих функций полезности количества потребляемых благ xi. При этом на первом этапе будем считать, что все блага являются благами разового потребления. Соответственно, функционал трансвременной полезности приобретает вид
67 V=VU1x11,…,xn1,…,UTx1T,…,xnT, (9)
68 где x1t,…,xnt — набор потребляемых экономическим агентом благ в период t (t = 1,…,T).
69 Возникают два вопроса, какие именно товары и в каких количествах должны стать предметом трансвременного обмена (натуральных кредитных отношений) и каким образом должны определяться пропорции трансвременно́го обмена.
70 В качестве объекта кредитных отношений можно взять любое благо. Дело в том, что при любом выборе оптимальная структура потребления в каждый период будет формироваться с учетом возможностей текущего обмена, тогда как для кредитных отношений важна величина меновой ценности, а не натуральная форма продуктов. С учетом этого удобно рассматривать выбранный для трансвременного обмена товар одновременно и как товар-счетчик для определения меновых ценностей остальных благ. Что касается пропорции трансвременного обмена, то она будет выражаться процентной ставкой в натуральном измерении.
71 Предполагаем, что в начальный момент каждого периода 1,…, T потребитель гарантированно получает в свое распоряжение один и тот же набор благ e = (e1, …, en). Для определенности можем считать его результатом производственной деятельности предыдущего периода. Пусть первое благо является товаром-счетчиком. Тогда вектор меновых ценностей будет иметь вид p = (1, p2, …, pn ). Далее исходим из того, что рассматриваемый экономический агент получает («+») (предоставляет («–»)) натуральный кредит в размере h1 в начальный момент первого периода на T периодов. При этом погашение кредита будет осуществляться заемщиком поставками первого блага в равных количествах в начальные моменты всех периодов времени, начиная со второго и заканчивая (T + 1)9.
9. Таким образом, при принятой нами схеме кредит, полученный / предоставленный в первый период, будет влиять на потребление и в периоде T+1.
72 Легко убедиться, что при такой схеме размеры соответствующих поставок товара-счетчика в каждый период должны составлять h1/Sr=x11-e1/Sr , где S(r)=∑t=2T+11/(1+r)t-1, r — процентная ставка 10.
10. Srate представляет собой сумму членов геометрической прогрессии, первый из которых равен дисконту D=1/1+rate , а последний DT=1/1+rateT . Ее величина может, соответственно, определяться по формуле Srate=D1-DT/1-D=1-1/1+rateT/rate . Легко заметить, что S→1/rate при T→∞.
73 Предполагаем, что текущий обмен происходит мгновенно в начале каждого периода с первого по T + 1. Поэтому полученные в результате его блага непосредственно влияют на величину полезности, извлекаемую потребителем в соответствующий отрезок времени. Количество блага  i , переданного («–») (полученного («+»)) в рамках текущего обмена в периоде t, будем обозначать zit.
74 При указанных выше условиях количество благ, потребляемых экономическим агентом в первый и во все последующие периоды, будет составлять:
75 первого блага в t = 1: x11 = e1 + h1 + z11; первого блага в t = 2,…,T + 1: x1t = e1t — h1 /S(r) + z1t ; остальных благ в t = 1,…,T + 1: xit = ei + zit, i = 2,…, n.
76 Легко убедиться в том, что все периоды, начиная со второго, оказываются близнецами в том смысле, что в их рамках величина потребления по всем видам благ одинаковая: U2=U3=⋯=UT+1 . Из природы текущего обмена следует, что суммарные величины меновых ценностей благ, которые потребитель в каждый период передает в обмен и получает из обмена, должны равняться друг другу; следовательно, z1t + p2z2t + ⋯+ pnznt = 0, t = 1,…,T + 1.
77 С учетом сказанного интересующая нас модель будет иметь вид:
78 maxV=V(U1,...,UT+1) (10)
79 при условиях11:
11. Так как вектор zt  один и тот же для всех t=2,…,T+1 , то в ограничениях представлен только один из них.
80 z11+p2z21+…+pnzn1=0, (11)
81 z1t+p2z2t+…+pnznt=0,     t=2,…,T+1, (12)
82 где U1=U1x11z11,h1,x21z21,…,xn1zn1, Ut=Utx1tz1t,h1,x2tz22,…,xntznt.
83 Построив функцию Лагранжа и приравнивая ее частные производные функции нулю, получаем необходимые условия наличия максимума у целевой функции. При этом учитываем, что ∂x11/∂h1=∂xit/∂zit=1 ,    t=1,…,T+1 , а ∂x1t/∂h1=-1/Sr t=2,…,T+1 . В результате:
84 Iz11=∂V∂U1∂U1∂x11+λ1=0, (13)
85 Izi1=∂V∂U1∂U1∂xi1+λ1pi=0,     i=2,…,n; (14)
86 Iz1t=∂V∂Ut∂Ut∂x1t+λt=0,     t=2,…,T+1; (15)
87 Izit=∂V∂Ut∂Ut∂xit+λtpi=0     i=2,…,n;    t=2,…,T; (16)
88 Ih1=∂V∂U1∂U1∂x11-T1Sr∂V∂Ut∂Ut∂x1t=0,     t=2,…,T+1; (17)
89 Iλ1=z11+p2z21+…+pnzn1=0; (18)
90 Iλt=z1t+p2z2t+…+pnznt=0,     t=1,…,T. (19)
91 Решение этой системы уравнений дает значения показателей текущей и трансвременной торговли, обеспечивающие максимизацию благосостояния соответствующего экономического агента при заданных величинах меновых ценностей и процентной ставки. Таким образом, эти параметры оказываются аргументами у функции и текущего, и трансвременного спросов: zit=zitp-,rate ,  h1=h1p-,rate .
92 Заметим, что в текущем обмене полностью сохраняют силу известные условия: в каждый период предельные нормы замещения одних благ другими должны равняться соотношению их меновых ценностей. В этом легко убедиться, если почленно разделить друг на друга два любых уравнения из (13)–(16) (уравнение (13) на (14), уравнение (15) — на следующее уравнение, характеризующее значение частной производной Лагранжа по z21 , и т.д.). Что же касается предельной нормы замещения настоящего будущим, то здесь возникает более сложная зависимость, чем та, которая проявляется при абстрагировании от отдельных благ при анализе эффекта трансвременного обмена.
93 Имея в виду, что ∂V∂U1/∂V∂Ut=∂Ut∂U1 , мы можем представить уравнение (17) в виде
94 ∂Ut∂U1=TSr∂Ut∂x1t/∂U1∂x11. (20)
95 Если предположить, что время, на которое предоставляется кредит, составляет один период (первый), то формула (20) приобретет вид12 ∂U2∂U1=1+r∂U2∂x12/∂U1∂x11. (21)
12. Не забываем, что кредит, предоставленный на один год, влияет на потребление второго года.
96 Левая часть уравнения — абсолютная величина предельной нормы замещения настоящего будущим, а правая — произведение единицы плюс процентная ставка на соотношение предельных полезностей блага-счетчика во втором и первом периодах13. С учетом двух гипотез — отказа от временного предпочтения и убывающей предельной нормы замещения настоящего будущим — мы можем заключить следующее:
13. В оптимальном положении взятые по модулю предельные нормы замещения благами друг друга равняются соотношению их меновых ценностей, поэтому второй множитель в правой части уравнения (21) может быть представлен соотношением предельных полезностей в эти периоды любого другого блага.
97 – при ∂U2∂x12/∂U1∂x11=11+r потребитель не будет заинтересован в установлении кредитных отношений  h1=0 ;
98 – при ∂U2∂x12/∂U1∂x11>11+r потребитель будет заинтересован в предоставлении кредита h1>0;
99 – при ∂U2∂x12/∂U1∂x11<11+r потребитель будет заинтересован в привлечении кредита h1<0.
100 Однако только один из этих вариантов совместим с рассматриваемой нами моделью. И доказать это можно следующим образом.
101 При отсутствии кредитных отношений текущий обмен приведет к тому, что потребление всех благ во все периоды будет одинаковым, а потому и оптимальная величина предельной полезности благ во все периоды будет одной и той же. Но если ∂U2∂x12/∂U1∂x11=1 , то предельная норма замещения настоящего будущим (условие отсутствия трансвременного обмена) может равняться минус единице только при r=0 . Констатация этого обстоятельства важна для выявления того, каким образом отличающаяся от нуля процентная ставка будет влиять на сравнительную оценку текущего и будущего потребления.
102 Продифференцируем (21) по величине процентной ставки:
103 ∂MRS2/1∂ r=∂U2∂x12/∂U1∂x11, (22)
104 где  ∂U2/∂U1=MRS2/1 .
105 Предельные полезности блага-счетчика ∂U1/∂x11 и ∂U2/∂x12 положительные, поэтому изменение процентной ставки приводит к аналогичному по направлению изменению абсолютной величины предельной нормы замещения полезности текущей полезностью будущей. Поэтому ∂U2/∂U1>1 при r>0 . С учетом гипотезы о квазивогнутости функции текущей полезности и, соответственно, выпуклости ее кривых безразличия это означает, что при любом положительном уровне процентной ставки потребитель будет заинтересован в предложении кредита. Этот вывод относится ко всем потребителям, формирование кредитных отношений становится невозможным, так как в рассматриваемых условиях отсутствуют экономические агенты, предъявляющие спрос на кредит. Они могут появиться лишь в случае если величина процентной ставки уйдет в отрицательную зону, но тогда исчезнут желающие предоставлять кредит.
106 Подводя промежуточный итог, мы можем констатировать следующее. После отказа от гипотезы о существовании у потребителя временно́го предпочтения исчезает симметрия в анализе текущего и трансвременного (чистого) обмена. И это, конечно, не случайно: в исходной ситуации предельная норма замещения текущей полезности будущей оказывается у всех экономических агентов одинаковой — равной минус единице. И тогда вполне естественным кажется вывод, что единственной возможностью обосновать появление чистого кредита является ссылка на различия в ожиданиях экономических агентов в отношении будущего благосостояния. В этом случае у них будет срабатывать стремление выравнивать уровень потребления. Подведение же более фундаментальных основ под теорию кредитных отношений и процентной ставки приходится связывать исключительно с выходом за рамки сферы обращения (Silberberg, 1990, p. 430–433).
107 2.2. Возможность, связанная с выделением особого класса потребительских благ
108 Между тем, имеется еще одна возможность выведения кредитных отношений из модели чистого трансвременного обмена. До сих пор мы исходили из того, что эффект от потребления имеет разовый характер. Это предположение совершенно справедливо в отношении таких благ как например, продукты питания. Но существуют блага, которые служат потребителю в течение длительного времени, — начиная от предметов домашней утвари и одежды и кончая жилищами и разнообразными домашними приспособлениями. В отличие от обычных благ приобретение таких предметов имеет инвестиционный характер и оказывается непосредственно связанным с трансвременной стороной системы индивидуальных предпочтений. Это обстоятельство дает основания предположить, что анализ обмена с участием таких благ позволит раскрыть условия существования чистых кредитных отношений, ввести понятие процентной ставки и раскрыть закономерности формирования ее равновесного уровня в рамках рассматриваемых условий.
109 Начнем с анализа модели, в которой потребительское благо длительного пользования является объектом обычной торговли, результатом которой становится смена собственников обмениваемых благ.
110 Пусть имеется n обычных (т.е. разового использования) благ, с номерами от 1 до n , причем благо под номером 1 выполняет функции блага-счетчика, и одно капитальное потребительское благо (его номер n+1 ), срок полезного действия которого составляет T периодов. На начало первого периода в распоряжении потребителя имеется набор благ (задается экзогенно), представленный вектором e=e1,…,en, en+1 . В этот момент рассматриваемый экономический агент совершает меновые сделки, направленные на максимизацию уровня его благосостояния, в результате которых в его распоряжении оказывается набор благ x=x11,…,xn1, xn+11 .
111 К началу каждого следующего периода ( t=2,…,T ) все обычные блага x1t,…,xnt полностью потребляются, и в распоряжении рассматриваемого нами индивидуума снова оказывается e1,…,en обычных благ14. Иначе обстоит дело с капитальным потребительским благом. Его количество xn+11 , полученное по итогам обмена, совершенного в начальный момент первого периода, сохраняется у потребителя на протяжении всех T периодов его существования15. Чтобы излишне не осложнять стоящую перед нами проблему, будем считать, что и потребляемое количество услуг этого блага будет одним и тем же в течение всех T периодов. Иными словами, капитальное благо не станет объектом обмена в начальные моменты t=2,…,T . С учетом этого вектор всех благ, которые будут у потребителя на начальные моменты t=2,…,T , примет вид e'=e1,…,en, xn+1 .
14. Нас не интересует их происхождение. Но при желании мы можем считать, что этот набор благ является результатом производственной деятельности экономического агента в течение предшествующего периода.

15. Мы можем считать, что в течение всего этого времени экономический агент постепенно создает соответствующие блага и поэтому они станут доступными лишь к началу периода T+1 .
112 Обратим внимание на важную особенность функции текущей полезности в условиях существования потребительских благ длительного пользования. Аргументом этой функции является не количество таких благ, а объем оказываемых ими услуг потребителю в течение соответствующего периода. Для простоты будем считать, что этот объем не меняется на протяжении всего срока существования капитального блага. При таком предположении объем услуг, оказанных в течение одного периода такими благами, можно измерять их количеством. Правда, надо иметь в виду, что размерность этих показателей разная: первый является потоковым, второй — моментным; при этом второй показатель служит основой первого. Поэтому объем услуг капитального блага xn+1* мы будем выделять звездочкой и рассматривать как функцию его количества: xn+1*=xn+1*xn+1 .
113 С учетом сказанного целевая функция нашей модели будет иметь вид:
114 max V=VU1x11,…,xn1,xn+11*xn+1,…,UTx1T,…,xnT,xn+1T*xn+1. (23)
115 Ограничения модели должны учитывать указанное выше различие между первым и остальными периодами, состоящее в том, что только в первом из них капитальное благо является объектом обмена:
116 x11-e1+p2x21-e2+…+pnxn1-en+pn+1xn+11-en+1=0, (24)
117 x1t-e1+p2x2t-e2+…+pnxnt-en=0,  (25)
118 где pi — меновая ценность потребительских благ ( i=2,…,n+1 ); t — любой из периодов, начиная со второго и заканчивая периодом T .
119 Строим функцию Лагранжа и, приравняв ее первые частные производные нулю, получаем необходимые условия наличия максимума у функции трансвременной полезности V :
120 Ixi1=∂V∂U1∂U1∂xi1+piλ1=0,     i=1,…,n; (26)
121 Ixit=∂V∂Ut∂Ut∂xit+piλ2T-1=0,     i=1,…,n,     t=2,…,T; (27)
122 Ixn+1=∑t=1T∂V∂Ut∂Ut∂xn+1t*+pn+1λ1=0; (28)
123 Iλ1=x11-e1+p2x21-e2+…+xn1-enpn+xn+11-en+1pn+1=0; (29)
124 Iλ2=x11-e1+p2x2t-e2+…+xnt-enpn=0. (30)
125 Представим уравнения (26) и (28) следующим образом (принимая во внимание, что p1=1 ):
126 ∂V∂U1∂U1∂x11=-λ1; (31)
127 ∑t=1T∂V∂Ut∂Ut∂xn+1t*=-pn+1λ1. (32)
128 Выражение в левой части (31) представляет собой предельную трансвременную полезность блага-счетчика в первый период, а выражение в левой части (32) — предельную трансвременную полезность капитального блага. Из (31) и (32) следует, что
129 ∑t=1T∂V∂Ut∂Ut∂xn+1t*/∂V∂U1∂U1∂x11=pn+1. (33)
130 Таким образом, для того чтобы в рассматриваемых условиях обеспечить максимальный уровень благосостояния, потребитель должен добиваться в первом периоде при помощи меновых сделок получения такого набора благ, который характеризуется пропорциональностью предельных трансвременных полезностей всех его компонентов (в том числе представляющих капитальные блага) их меновым ценностям. Во всех остальных периодах данное требование распространяется исключительно на блага разового потребления (см. формулу (27)), поскольку обмен капитальными благами в их рамках не производится. В результате оказывается, что характерный для этих временных отрезков оптимальный набор благ отличается от набора первого периода.
131 Последнее обстоятельство дает основание предположить, что участник обмена увеличил бы свое благосостояние еще больше, если бы дополнительно получил возможность выравнять уровень потребления всех благ в первом и остальных периодах. Оказывается, что имеется даже не один, а два способа решения этой задачи при помощи изменений институционального характера.
132 Первый из этих способов связан с превращением в самостоятельный объект обмена услуг, предоставляемых капитальными благами. В таком предположении нет ничего выходящего за разумные рамки: фактически мы всего лишь допускаем возможность сдачи таких благ в аренду. Как следует из модели чистой торговли, в состоянии общего равновесия все блага будут таким образом распределены между членами общества, что их меновые ценности окажутся равными предельным нормам замещения этих благ товаром-счетчиком. Такой же вывод применим и к услугам блага длительного пользования, с той особенностью, что меновая ценность pn+1* будет опираться на их предельную полезность ∂Ut/∂xn+1t* , производную от того количества капитального блага, которое потребитель фактически использует — независимо от того, находятся ли они в его собственности или нет. Иными словами, если величина арендуемых услуг этого блага составляет zn+1t* , то его потребление равно xn+1t*=en+1*+zn+1t* .
133 В условиях, когда возможна аренда услуг, предоставляемых благами длительного пользования, вектор потребления будет одинаковым во все периоды: x1t,…,xnt,xn+1t* . Следовательно, одинаковыми будут и арендные платежи, осуществляемые в форме поставок товара-счетчика. Их величина составит pn+1*zn+1*=pn+1*xn+1*-en+1* (нижний индекс t мы убрали, так как величины аренды и потребления капитального блага теперь одинаковы во все периоды).
134 Потребитель в начале каждого периода ( t=1,…,T ) берет (сдает) в аренду одно и то же количество капитального блага, поэтому услуги последнего в течение всего срока его функционирования будут в точности такими же, как и тогда, когда экономический агент в самом начале являлся бы собственником соответствующего количества этого блага: xn+11=en+1+zn+11 . Иными словами, поток равных по величине арендных платежей pn+1*zn+1* , осуществляемых в начальный момент периода, следующего за использованием потребительского блага, может рассматриваться как альтернативные издержки (выгоды), связанные с изменением заданного экзогенно количества капитального блага en+1 при условии, что во все периоды на одинаковом (оптимальном) уровне будет также находиться количество остальных благ.
135 Отсюда вытекает возможность альтернативного — по отношению к аренде — решения задачи выравнивания уровня благосостояния. Речь идет об использовании с этой целью кредитных отношений, объектом которых становится капитальное благо: ведь поток равных по величине арендных платежей в течение всего срока функционирования потребительского блага длительного пользования легко может быть замещен потоком таких же платежей по обслуживанию натурального кредита16. Легко убедиться, что погашение кредита равными платежами предполагает, что величина соответствующих поставок товара-счетчика в каждый период, начиная со второго и заканчивая периодом T , должна составлять pn+1hn+1/Sr=pn+1xn+1-en+1/Sr, где hn+1 — число привлекаемых (+) (предоставляемых (–)) в кредит единиц капитального блага. В этих условиях целевая функция потребителя и ограничения, с которым ему приходится сталкиваться, будет иметь вид
16. Мы предположили, что арендные платежи за пользование капитальным благом осуществлялись в каждый период (1,…,T), поэтому мы должны этот же подход использовать и применительно к кредитным отношениям. Это означает, что платежи по обслуживанию кредита теперь осуществляются в начальный момент каждого периода (1,…,T). В результате отпадает необходимость учитывать потребление в периоде Т+1 : к его началу положение дел возвращается к тому, каким оно было на начало периода 1.
136 maxV=VU1e1-hn+1pn+1/S(rate)+z11,  e2+z21,...,en+zn1,x*(n+1)1(en+1+hn+1),...,UTe1-hn+1pn+1/S(rate)+z1T,  e2+z2T,...,en+znT,x*(n+1)T(en+1+zn+1)] (34)
137 при условии z1t+p2z2t+…+pnznt=0,     t=1,…,T. (35)
138 Ниже приводятся приравненные нулю частные производные функции Лагранжа, построенной на основе целевой функции (34) и ограничений (35). Следует иметь в виду, что все T периодов являются близнецами в том смысле, что в их рамках уровни потребления благ, а следовательно, и их предельные полезности ∂Ut/∂xit совпадают. В силу динамической состоятельности целевой функции не различаются также и предельные трансвременные полезности ∂V/∂Ut отдельных периодов:
139 Iz1t=∂V∂Ut∂Ut∂x1t+λT=0,      t=1,…,T; (36)
140 Izit=∂V∂Ut∂Ut∂xit+λTpi=0,     i=2,…,n;     t=1,…,T; (37)
141 Ihn+1=∑t=1T∂V∂Ut∂Ut∂xn+1t*-∂Ut∂x1tpn+1Sr=0; (38)
142 Iλ=z1t+p2z2t+…+pnznt=0,     t=1,…,T. (39)
143 Из nT уравнений, представленных формулами (36)–(37), вытекает известный вывод: в оптимальном положении предельные нормы замещения благ друг другом равняются соотношениям их меновых ценностей. Но особый интерес для нас имеет формула (38), из которой легко получить равенство
144 ∂Ut∂xn+1t*/∂Ut∂x1t=pn+1Sr. (40)
145 За предельными полезностями услуг капитального блага и блага счетчика, представленными в левой части формулы (40), стоят их оптимальные количества. Более того, эта формула в неявной форме предполагает оптимальные количества и всех других благ, поскольку они также составляют неотъемлемую особенность положения, при котором потребитель максимизирует величину трансвременной полезности. Состав этого оптимального набора зависит от исходного количества благ, имевшихся в распоряжении экономического агента (вектор e-), и вектора их меновых ценностей p- .
146 Таким образом, можно заключить, что величина индивидуального чистого спроса на кредит является функцией процентной ставки, вектора меновых ценностей всех благ и их исходного количества, имеющегося в распоряжении потребителя:
147 hn+1=hr,p1,…,pn+1,e1,…,en+1. (41)
148 Для того чтобы определить, как изменение процентной ставки влияет на размеры чистого спроса, поступим следующим образом. Опираясь на формулу (40), представим предельную полезность услуг капитального блага ∂Ut/∂xn+1t* как функцию выражения pn+1/Sr и предельной полезности блага-счетчика ∂Ut/∂x1t , и продифференцируем ее по r:
149 ∂Ut∂xn+1t*'n=-1Sr2pn+1∂Ut∂x1tS'r. (42)
150 Так как сумма дисконтов S — убывающая функция от процентной ставки, то изменение последней будет вести к изменению в том же направлении и величины предельной полезности услуг капитального блага. Поэтому в нормальных условиях, т.е. в условиях, когда действует закономерность убывающей предельной полезности, рост процентной ставки будет приводить к уменьшению чистого спроса на капитальное благо и, соответственно, на его привлечение при помощи кредитных отношений. Противоположная ситуация будет иметь место при снижении процентной ставки. А это означает, что функция индивидуального чистого спроса hn+1 является убывающей по размеру процентной ставки.
151 Важное значение имеет уровень процентной ставки r0 , при котором чистый спрос потребителя на кредит будет равняться нулю. Этот уровень вытекает из формулы (40), отражающей оптимальное положение, в котором возможности текущего и трансвременного обмена полностью исчерпаны. Поэтому если в этой ситуации происходит увеличение процентной ставки, потребитель оказывается заинтересованным предложить капитальное благо в кредит; если же процентная ставка снижается, потребитель начинает предъявлять спрос на заимствование капитального блага.
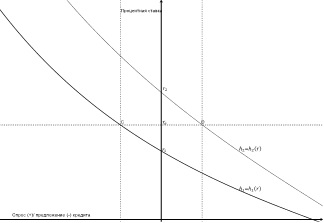
152 Поскольку у различных потребителей процентная ставка, при которой чистый спрос на кредит равняется нулю, может совпадать лишь случайно, становится очевидной их вероятная заинтересованность вступить в отношения, связанные с заимствованиями капитального блага. Механизм формирования таких отношений можно наглядно представить графически (см. рисунок).
153

Рисунок. Графическое представление условий формирования кредитных отношений
154 Кривые h1= h1r и h2= h2r представляют функции чистого спроса на натуральный кредит двух экономических агентов. При r=r1 участвовать в кредитных отношениях не будет заинтересован первый потребитель, при r=r2 — второй. Если r<r1 , то оба потенциальных участника сделки будут заинтересованы в получении кредита, а при r>r2 — в предоставлении кредита. Таким образом, кредитные отношения между этими двумя потребителями будут иметь место только в случае, когда r1<r<r2 , причем первый экономический агент будет выступать в качестве кредитора, а второй — в качестве заемщика. Процентная ставка re является равновесной, поскольку размер кредита AO , в предоставлении которого заинтересован первый потребитель, равняется размеру кредита OB , в получении которого заинтересован второй.
155 Проведенный анализ свидетельствует о том, что оба подхода к максимизации уровня благосостояния потребителя — при помощи аренды услуг капитальных благ и при помощи их превращения в объект кредитных отношений — эквивалентны. Но отсюда прямо вытекает и возможность сочетать эти две формы получения (предоставления) доступа к услугам капитальных благ без потерь в уровне благосостояния экономического агента. Анализ такой смешанной ситуации позволяет выявить взаимосвязь между размерами арендной платы, меновой ценности капитального блага и процентной ставкой. Поскольку
156 ∂Ut∂xn+1t*/∂Ut∂x1t=pn+1*,
157 формула (40) может быть трансформирована в
158 pn+1*Sr=pn+1. (43)
159 Таким образом, мы приходим к известному (прежде всего применительно к капитальным благам производственного характера) выводу, в соответствии с которым в равновесном состоянии меновая ценность капитального блага равняется суммарному дисконтированному потоку меновых ценностей предоставляемых им услуг. Равенство левой и правой частей формулы будет достигаться в конечном счете благодаря конкуренции между арендой услуг благ длительного пользования и их классическим обменом.
160

3. Выводы
161 Основные результаты проведенного исследования можно суммировать следующим образом.
162 1. Удалось показать, что в число условий кредитных отношений не входит существование денег. Иными словами, кредит логически предшествует деньгам, а не наоборот17. А это означает, что в рамках чистой экономической теории категория кредита может (а потому и должна!) вводиться уже на стадии анализа простой меновой экономики, т.е. экономики, основанной на натуральном обмене.
17. Этот вывод в некотором смысле созвучен кредитной (долговой) теории денег, представленной, в частности, в (Macleod, 1889–1891; Mitchell-Innes, 1913; Graeber, 2011). Между тем, в контексте настоящей статьи он никакого отношения к этой теории не имеет.
163 2. Избранная методология исследования позволяет высветить важное отличие между текущим и трансвременным обменами: первый обеспечивает формирование оптимальной структуры текущего потребления, а второй — наилучшее распределение во времени совокупных меновых ценностей, которыми потребитель располагает в различные моменты (периоды). В силу последнего обстоятельства оказывается, что трансвременной обмен, в отличие от текущего, безразличен к натуральной форме блага, являющегося объектом сделки: предметом отношений заимствования может быть любой товар. По этой причине после появления денег эта роль естественным образом фактически закрепляется за ними.
164 3. Уже на этой стадии анализа выявляется неразрывная связь между текущим и трансвременным обменом. Поэтому в функционале трансвременно́й полезности в качестве аргументов функций полезностей отдельных периодов имеет смысл рассматривать конкретные потребительские блага, а не показатель агрегированного потребления или денежный доход. Только в этом случае можно увидеть взаимную обусловленность текущего и трансвременно́го обменов, пропорций текущего обмена и процентной ставки.
165 4. Как представляется, в статье окончательно решен вопрос о возможности обнаружения достаточных условий для формирования кредитных отношений на основе анализа исключительно сферы обращения, без апелляции к процессам, происходящим в производственной сфере.
166 Проводившиеся ранее исследования ориентировались на два возможных способа решения этой проблемы, однако в каждом были обнаружены уязвимые пункты. Первый, основанный на объединении в единой функции полезности текущих и будущих благ, размывает различие между текущим и трансвременным обменом, пропорциями текущего обмена и процентной ставкой. Второй, связанный с допущением наличия у потребителей временно́го предпочтения, построен на отказе (по крайней мере — частичном) от гипотезы рационального экономического агента (потребитель здесь оказывается близоруким).
167 В статье показана возможность решить проблему чистого кредита, возникающую в случае выделения из мира потребительских благ товаров длительного пользования (капитальных потребительских благ)18. Поскольку приобретение таких благ является актом инвестирования, то кредит превращается в инструмент повышения благосостояния потребителя.
18. В исследованиях, касающихся эволюции потребления на разных стадиях жизни индивида и возможностей его выравнивания, традиционно придается значение вопросу о так называемых долговечных благах (durable goods). Так, П. Самуэльсон писал: «Для целей настоящего исследования я делаю экстремальное допущение, что ничто не поддается хранению (nothing will keep at all). Таким образом, никакая трансвременная торговля с Природой невозможна (т.е. для всех обменов такого рода мы имели бы i=-1! [здесь i — процентная ставка. — А.Н.]). Если бы Робинзон Крузо был одинок, то он, очевидно, умер бы, как только достиг пенсионного возраста (at the beginning of his retirement years)» (Samuelson, 1958, p. 468). Как мы видим, речь здесь идет не о капитальных потребительских благах, порождающих поток потребительских услуг, а о поддающихся длительному хранению обычных благах.
168 5. Существование чистых кредитных отношений не должно рассматриваться ни как доказательство симметричности процессов, происходящих в рамках текущего и трансвременного обменов, ни как аргумент в пользу отказа от учета процессов, протекающих в производственной сфере. Выше было отмечено, что чистый текущий и трансвременно́й обмены, будучи неразрывно связанными друг с другом, имеют разные основания и потому прямой параллели между ними проведено быть не может. Точно так же выявление производственных корней кредитных отношений никак не теряет своей значимости из-за того, что также удалось обнаружить и иные условия их возникновения.
169 Существенно важно другое. Во-первых, мы теперь точно знаем ту стадию, на которой кредитные отношения впервые могут быть введены в анализ, что, как отмечалось в начале статьи, имеет большое значение для чистой экономической теории. Во-вторых, были выявлены причины, приводящие к возникновению особой формы трансвременно́го обмена — потребительского кредитования. И, наконец, в-третьих, можно утверждать, что у потребительского и производственного кредитов обнаруживается единая основа, связанная с их использованием в инвестиционных целях.

Библиография

1. Некипелов А. (2006). Становление и функционирование экономических институтов. От «робинзонады» до рыночной экономики, основанной на индивидуальном производстве. М.: Экономистъ.

2. Некипелов А. (2017). Общая теория рыночной экономики: учебник. М.: Магистр.

3. Некипелов А. (2019а). Кризис в экономической науке — природа и пути преодоления // Вестник Российской академии наук. Т. 89. № 1. СС. 24–37.

4. Некипелов А. (2019б). Модель робинзонады как исходный пункт чистой экономической теории // Экономика и математические методы. Т. 55. № 3. С. 5–20.

5. Allais M. (1947). Economie et Interet. Presentation Nouvelle des Problemes Fondamentaux Relatifs au Role Economique du Taux de l’Interet et de leur Solutions. Paris. Depositaire. Librarie des Publications Officielle.

6. Barro R. (1989). The Ricardian Approach to Budget Deficits. Journal of Economic Perspectives, 3, 37–54.

7. Bliss C. (1975). Capital theory and the distribution of income. Amsterdam: North-Holland.

8. Bo?hm-Bawerk E. (1890). Capital and interest, a critical history of economical theory. London, N.Y.: Macmillan and Co.

9. Fisher I. (1930). The theory of interest. New York. August M. Kelley (1st edition. N.Y.: The Mac-millan Co., 1930)).

10. Fisher I. (1970). The theory of interest. N.Y.: August M. Kelly.

11. Gale D. (1973). On the theory of interest. American Mathematical Monthly, 88, 853–868.

12. Graeber D. (2011). Debt: The first 5000 years. Brooklyn, N.Y.: Melville House.

13. Katzner D.W. (2006). An introduction to the economic theory of market behavior. Microeconomics from a Walrasian perspective. Chaltenham, Northampton: Edward Elgar.

14. Koopmans T. (1960). Stationary Ordinal Utility and Impatience. Economtrica, 28, 287–309.

15. Macleod H. (1889–1891). The theory of credit. London: Longmans, Green, and Company.

16. Malinvaud E. (1953). Capital accumulation and efficient allocation of resources. Econometrica, 21, 223–268.

17. Mas-Colell A., Whinston M., Green J. (1995). Microeconomic theory. New York: Oxford Univer-sity Press.

18. Mises L. von (1971). The theory of money and credit. N.Y.: The Foundation for Economic Educa-tion, Irvington-on-Hudson.

19. Mitchell-Innes A. (1913). What is money? The Banking Law Journal, May, 377–408.

20. Ramsey F. (1928). A mathematical theory of saving. Economic Journal, 38, 543–549.

21. Samuelson P. (1958). An exact consumption — loan model of interest with or without the social contrivance of money. The Journal of Political Economy, 66, 6, 467–482.

22. Silberberg E. (1990). The structure of economics. A mathematical analysis. 2st edition. N.Y.: McGraw-Hill Publishing Company.

23. Solow R. (1956). A Contribution to the Theory of Economic Growth. Quarterly Journal of Economics, 70, 65–94.

24. Strotz R. (1956). Myopia and inconsistency in dynamic utility maximization. Review of Economic Studies, 23 (3), 165–180.

25. Swan T. (1956). Economic growth and capital accumulation. Economic Record, 32, 334–361.

26. Weizsacker C. (1971). Steady state capital theory. N.Y.: Springer-Verlag.

Комментарии

Сообщения не найдены

Написать отзыв
Перевести