- PII
- S042473880019186-3-1
- DOI
- 10.31857/S042473880019186-3
- Publication type
- Article
- Status
- Published
- Authors
- Volume/ Edition
- Volume 58 / Issue 2
- Pages
- 54-63
- Abstract
One of the main branches of economy in Tuva republic is cattle breeding which has developed historically on the basis of Tuva’s geographical position, climate and environmental conditions and centuries-old experience of Tuvinian population. Ethno-economic custom of Tuvinian people together with the governmental support lay the groundwork for the development of regional industrial clusters such as the DUK project (processing of sheep wool and goat hair) and the KESH project (currying of animal skins). In order to raise marketability and promote industrial development on the whole, it seems reasonable to organize groups of manufacturing clusters in the region, which would unite factories dealing with processing of raw materials supplied by traditional ethnic households. The aim of this work is to define optimal geographical coordinates for manufacturing facilities taking into account the location of raw material suppliers, to the effect of minimizing transportation costs. The authors suggest a mathematic model of optimal economic space layout on the basis of the development of traditional industrial system. Cluster analysis apparatus was used as well as logistic approach to formation of production and distribution network taking into account the existing transport infrastructure. Calculations were made using the example of organization and development of Tuvinian light industry cluster based on traditional for this region branch of economy, sheep breeding
- Keywords
- ethnoeconomics; agro-processing; industrial development; mathematical model; optimization; ethnocluster; the shortest path problem; logistics
- Date of publication
- 18.06.2022
- Year of publication
- 2022
- Number of purchasers
- 11
- Views
- 548
Введение Повышению качества жизни населения регионов и конкурентного преимущества традиционной хозяйственной системы с сохранением этнокультурной идентичности способствует этноэкономика, которая является перспективным направлением изучения проблем экономического развития национальных республик с учетом географических, исторических и культурных особенностей этнического сообщества. Под термином «этноэкономика» понимают науку о взаимодействии культур, традиций, этноса, обычаев, идеологии, религиозных взглядов различных наций с их хозяйственной деятельностью (Клочко, Кобозева, 2017:39). Исследователями обозначены три главных направления ее развития (Ахметов, Бердникова, Салихова, 2012:83):
- Индустриально-этническое (промышленная переработка сельскохозяйственного сырья);
- Традиционно-этническое (развитие народных промыслов и ремесла, сельского хозяйства);
- Рыночно-этническое (развитие этнотуризма).
МЕТОДЫ В управлении бизнес-процессами важное значение имеют интегрированные математические модели (транспортно-складская модель и производственно-транспортно-складская модель), которые позволяют реализовать принцип глобальной оптимизации. Анализ литературных источников показывает, что для интегрированных моделей, как правило, дается математическая постановка в виде задачи смешанного целочисленного линейного программирования (с целочисленными и булевыми переменными). При нахождении численного решения данной задачи возникает ряд вычислительных проблем, так как в настоящее время не разработаны достаточно эффективные с вычислительной точки зрения алгоритмы поиска решения. Кроме того, данная постановка задачи не решает вопроса определения оптимального места расположения производств с точки зрения минимизации транспортных издержек. Вышеперечисленное и обуславливает актуальность разработки новых альтернативных интегрированных математических моделей оптимизации бизнес-процессов. Вопросам построения интегрированных моделей логистических систем посвящены работы исследователей А.А. Бочкарева, В.С. Лукинского, В.И. Сергеева, В.В. Дыбской, Шапиро Дж. и других. Модели транспортно-складских задач, которые относятся к вышеуказанному классу моделей, как видно из названия, состоят из двух подмоделей: транспортной модели и модели определения географических координат расположения складов (или производственных мощностей), при которых оптимизируются транспортные издержки. Задача определения координат расположения складов (производственных мощностей) на территории рассматриваемой местности (региона, макрорегиона, страны и т.д.) вызывает большой интерес у исследователей и является одной из фундаментальных задач логистики как науки. Исходными данными поставленной задачи являются: координаты поставщиков (xi, yi); объемы поставляемой (Qi) и потребляемой (Pj) продукции; а также информация о транспортной инфраструктуре рассматриваемой местности. Решение задачи в непрерывной постановке заключается в определении точной географической локации склада с координатами (x, y), при которых оптимизируются логистические расходы, представляющие собой сумму произведений расстояния от поставщиков до склада на удельный вес (объем) транспортируемого груза (Монгуш, 2019). Для регионального размещения производственных объектов и оптимальной организации экономических промышленных этнокластеров авторы предлагают воспользоваться разработанной ими постановкой и подходом к решению транспортно-складской задачи (Богданов, Монгуш, 2018) и производственно-транспортно-складской задачи (Богданов, Монгуш, 2019). В принципе с математической точки зрения транспортно-складская задача практически идентична производственно-транспортной задаче и обе эти задачи являются частным случаем задачи размещения. При нахождении координат расположения нескольких производственных объектов или складов представляется естественным определение скоплений поставщиков сырья и потребителей продукции предприятия (кластеров) и назначения центров для обслуживания этих кластеров, что будет способствовать уменьшению стоимости перевозок и, соответственно, увеличению прибыли предприятия. В качестве поставщиков сырья рассматриваются сельскохозяйственные организации, индивидуальные предприниматели и крестьянские хозяйства, объединенные по признаку принадлежности к конкретному муниципальному образованию (району). Рассмотрим математическую постановку задачи. Введем следующие обозначения: Vi - объем вывозимого сырья от i-го поставщика (i=1, …, n); Gk - множество поставщиков для k-го производства (k=1, …, m); qk - объем производства продукции на k-ом производстве; p - цена выпускаемой продукции; AVC - средние переменные издержки на производство единицы выпускаемой продукции; FCk - постоянные издержки k-го производства. Тогда прибыль от реализации продукции (без учета затрат на транспортировку) для k-го производства составит (1) где (2) - коэффициент, учитывающий нормы расхода сырья на единицу конечного продукта. Затраты на транспортировку сырья для k-го производства составят (3) где - расстояние от i-го поставщика до k-го производства; - стоимость перевозки единицы веса на единицу расстояния. Сформулируем критерий оптимизации рассматриваемой задачи (4) Преобразуем критерий (4) к виду (5) Далее
где
а постоянные затраты всех производств будем считать одинаковыми. Таким образом, критерий оптимизации примет вид (6) или (7) Решаемая задача связана с поиском оптимального разбиения поставщиков на группы обслуживания производств Gk (k=1,…, m) и с определением места расположения предприятий. В задаче кластеризации объектов – производителей или потребителей продукции предприятия, как правило, мерой расстояния между объектами является физическое расстояние между ними, определяемое по формуле евклидова расстояния
где xi, yi – координаты i-го поставщика; x, y – координаты размещения производства. Безусловно это допущение не учитывает существующую сеть дорог (движение по прямой через леса и поля вряд ли возможно), но оно широко распространено в литературе по логистике, а любая математическая модель всегда является некоторым упрощением реальности – что-то учитывает, а чем-то пренебрегает. Можно принять допущение, что соотношение расстояния поездки по дорогам и по прямой одинаково для всех пар пунктов. При каждом задаваемом количестве производственных объектов m задача сводится к оптимизации разбивки всех поставщиков сырья на группы обслуживания объектов Gk (k=1,…,m) и по определению точек их месторасположения. При некотором текущем разбиении поставщиков на группы обслуживания производственных объектов задача определения их оптимального расположения может решаться независимо для всех зон обслуживания, исходя из минимизации суммарных затрат (7). Рассмотрим задачу минимизации затрат при доставке сырья в производственные объекты (координаты (x, y)) из ряда пунктов с координатами (xi, yi) ( ). Задача сводится к минимизации функции
по переменным х и у. Это достигается решением следующей системы уравнений Для численного решения систем нелинейных уравнений обычно используются итерационные методы: метод простой итерации, метод Зейделя, метод Ньютона. Для решения данной системы двух нелинейных уравнений будем использовать метод Ньютона. Алгоритм метода Ньютона для системы из двух уравнений с двумя неизвестными применительно к задаче нахождения оптимального места расположения склада приведен в одной из наших работ (Баисов И.М., Никитина Л.Н., Богданов А.И., 2017). При решении задачи нахождения координат расположения нескольких производственных объектов, под разбивкой потребителей на зоны обслуживания заданного m количества объектов понимают отыскание такого набора подмножеств G1, G2,…, Gm натурального ряда чисел 1, 2, …, n, что , а . Минимизация критерия качества кластеризации (как по разбиению поставщиков сырья на группы обслуживания производственного объекта, так и по выбору места расположения производственных объектов) отвечает требованиям такого разбиения поставщиков, когда в одной группе оказываются наиболее близкие между собой поставщики сырья. В то же время в качестве координат производственных объектов будут выбираться такие, которые минимизируют суммарные затраты на перевозки в зоне их обслуживания. С другой стороны, считая известными координаты производственных объектов, нетрудно построить разбиение G1, G2, ..., Gm, минимизирующее критерий качества кластеризации, при фиксированных координатах объектов, а именно (Проценко Ол., Проценко Ив, 2012) Для одновременного нахождения оптимального разбиения G1, G2, …,Gm и оптимального набора координат производственных объектов предлагается итерационный алгоритм, последовательно осуществляющий выбор оптимальных (по отношению к разбиению, полученному на предыдущем шаге) координат объектов, а затем разбиения, оптимального при местах расположения производственных мощностей, полученных на предыдущем шаге. Предложенный алгоритм по существу является некоторой модификацией алгоритмов кластерного анализа с оптимизацией критерия, в качестве которого вместо обычно используемых суммы внутриклассовых дисперсий или суммы попарных внутриклассовых расстояний используется экономический показатель – минимизация затрат. Как и все алгоритмы кластерного анализа с оптимизацией критерия, он не гарантирует сходимости именно к глобальному экстремуму. Чтобы снизить вероятность сходимости к локальному минимуму можно действовать двумя способами: - многократно генерировать случайным образом начальное разбиение объектов на кластеры; - в качестве начального разбиения принять результат, полученный классическим алгоритмом кластерного анализа агломеративного типа, который, скорее всего, будет близок к оптимальному.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЯ Этноэкономические кластеры легкой промышленности Республики Тыва (РТ) Деловая активность РТ, как правило, сконцентрирована преимущественно в столице региона – г. Кызыл, где расположено около 54 % предприятий республики. Здесь же осуществляется прием сельскохозяйственного сырья для дальнейшей переработки на предприятиях республики и других регионов. Для фермеров отдаленных районов, например Овюрского, Сут-Хольского, Бай-Тайгинского, Монгун-Тайгинского и других, это сопряжено с дополнительными высокими расходами на транспортировку. Эти расходы не всегда оправданы. Поэтому владельцам небольших хозяйств невыгодно возить в столицу свою продукцию. Зачастую они физически избавляются от шкур, шерсти, если сами их не перерабатывают. Поэтому организация пунктов сбора сельскохозяйственного сырья в районных центрах может снизить стоимость самого сырья для производства конечного продукта. Формирование и развитие этнокластеров легкой промышленности в РТ связано с переработкой продукции ведущей отрасли экономики республики – сельского хозяйства (шерсти и шкуры). В связи с неразвитостью дорожной инфраструктуры региона и транспортных услуг, в данной работе предложена организация пунктов первичного сбора и переработки шерсти и шкуры в административных центрах каждого муниципального образования республики (районных центрах). Это объясняется наличием развитой дорожной сети с покрытием регионального и федерального значения между административными центрами и городами. Для решения задачи кластеризации муниципальных образований РТ и формирования этноэкономических транспортно-логистических кластеров в таблице 1 представлены данные о географических координатах районных центров Тувы, которые могут служить центрами сбора сельскохозяйственного сырья у организаций, крестьянских хозяйств, хозяйств населения, а также объемы производства шерсти этих районов. Таблица 1. Географические координаты районных центров РТ1 и производство шерсти2
| № п/п | Муниципальный район (кожуун) | Районный центр | Координаты районных центров | Производство шерсти в год, тонн | |
| X | Y | ||||
| Муниципальные районы | |||||
| 1 | Бай-Тайгинский | с. Тээли | 90,2090 | 51,0149 | 152 |
| 2 | Барун-Хемчикский | с. Кызыл - Мажалык | 90,5704 | 51,1431 | 80 |
| 3 | Дзун-Хемчикский | г. Чадан | 91,5659 | 51,2845 | 117 |
| 4 | Каа-Хемский | с. Сарыг – Сеп | 95,5564 | 51,4943 | 21 |
| 5 | Кызылский | пгт. Каа-Хем | 94,5742 | 51,6995 | 127 |
| 6 | Монгун-Тайгинский | с. Мугур – Аксы | 90,4445 | 50,3786 | 76 |
| 7 | Овюрский | с. Хандагайты | 92,0685 | 50,7310 | 131 |
| 8 | Пий-Хемский | г. Туран | 93,9161 | 52,1473 | 34 |
| 9 | Сут-Холский | с. Суг – Аксы | 91,2891 | 51,4111 | 108 |
| 10 | Тандинский | с. Бай-Хаак | 94,4630 | 51,1661 | 35 |
| 11 | Тере-Холский | с. Кунгуртуг | 97,5214 | 50,5953 | 3 |
| 12 | Тес-Хемский | с. Самагалтай | 95,0081 | 50,6123 | 75 |
| 13 | Тоджинский | с. Тоора – Хем | 96,1273 | 52,4668 | 1 |
| 14 | Улуг-Хемский | г. Шагонар | 92,9111 | 51,5104 | 63 |
| 15 | Чаа-Холский | с. Чаа – Хол | 92,3636 | 51,5242 | 32 |
| 16 | Чеди – Холский | с. Хову – Аксы | 93,6763 | 51,1275 | 40 |
| 17 | Эрзинский | с. Эрзин | 95,1625 | 50,2589 | 168 |
| городские округа | |||||
| 18 | г. Кызыл | 94,4454 | 51,7239 | 2 | |
| 19 | г. Ак-Довурак | 90,5926 | 51,1741 | 11 | |
| ИТОГО | 1276 |
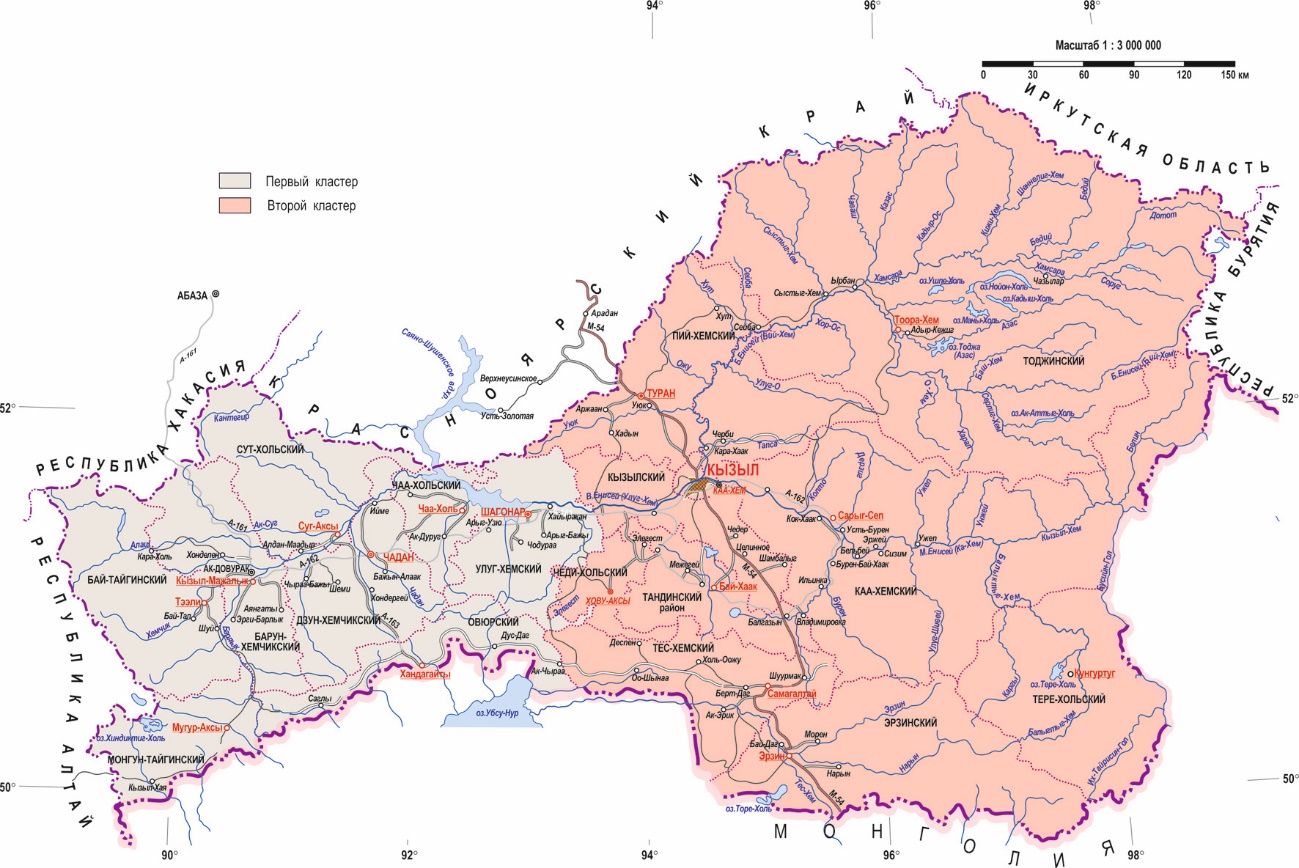
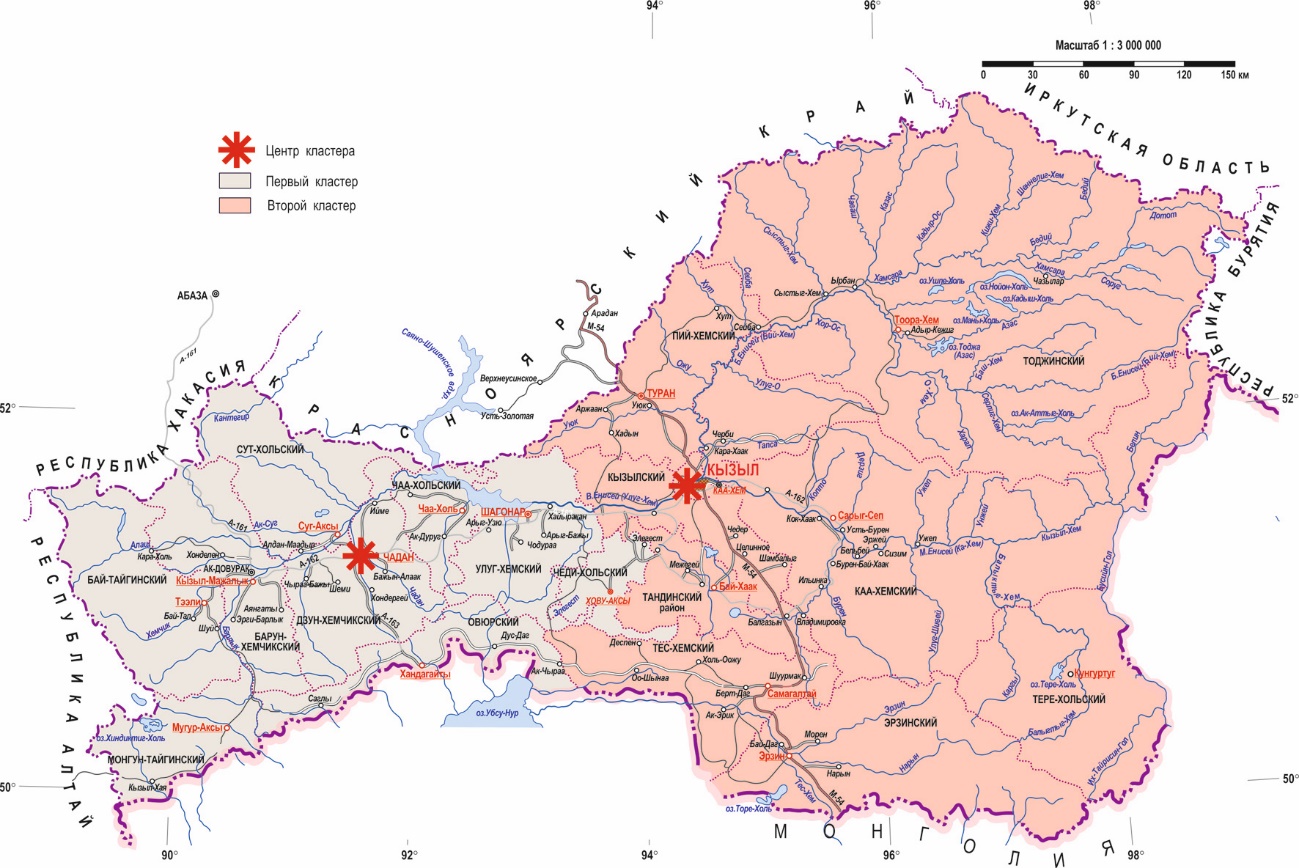
Для решения оптимизационной задачи с помощью компьютерной программы EXCEL и языка программирования VBA проведены расчеты по кластеризации муниципальных районов РТ. В случае одного производства его целесообразно разместить в точке с координатами (92,65; 51,05). При этом суммарный пробег машин составит 2281,91 т.км, а затраты на транспортировку (при характерном для РТ тарифе С = 25 руб/т.км ) – 57,05 тыс. руб. Общие затраты с учетом FC = 18 тыс. руб. составят 75,05 тыс. руб. В случае 2-х производств уже необходимо разделить все районные центры на 2 группы обслуживания (кластеры). Первоначальное разбиение было получено с помощью классического алгоритма кластерного анализа агломеративного типа (имеющаяся в свободном доступе в интернете программа реализует принцип «дальнего соседа»). В первый кластер попали 9 объектов с номерами 1, 2, 3, 6, 7, 9, 14, 15, 19, а во второй кластер – 10 объектов с номерами 4, 5, 8, 10, 11, 12, 13, 16, 17, 18. Рисунок 1. Первоначальное разбиение на кластеры Уже после первого шага работы нашего итерационного алгоритма получено оптимальное решение, в котором объект № 15 перенесен из первого кластера во второй. Оптимальные координаты расположения для первого предприятия (91,34; 51,10), а для второго – (94,18; 50,98). При этом суммарный пробег машин составил 1464, 74 т.км, а затраты на транспортировку – 36,62 тыс. руб. Общие затраты с учетом 2 FC= 36 тыс. руб. составят 72,62 тыс. руб. При трех кластерах с оптимальными координатами (91,05; 51,01), (92,42; 51,42), (94,98; 50,72) суммарный пробег машин еще снижается и составляет 917,76 т.км, а затраты на транспортировку – 22,94 тыс. руб. Однако общие затраты с учетом 3 FC возрастают и составят 76,94 тыс. руб. Таким образом, оптимальным оказался вариант с двумя производствами. В результате получено следующее деление кожуунов республики на 2 кластера поставщиков сырья для производства готовой продукции и рассчитаны координаты центров полученных кластеров – географические координаты оптимального расположения производственных объектов (фабрики, комбината, цеха) глубокой переработки сырья сельхозпроизводителей: I кластер – 7 кожуунов: Бай-Тайгинский, Барун-Хемчикский, Дзун-Хемчикский, Монгун-Тайгинский, Овюрский, Сут-Холский, Улуг-Хемский и г. Ак-Довурак с центром в точке с координатами (91,34; 51,10), округленными до координат г. Чадаан. В данный кластер вошли западные районы республики с наиболее развитым сельским хозяйством. Объем производства предприятий сельского хозяйства полученного макрорайона, а именно животноводства, составил в 2019 году 51,2 % общего объема региона (Социально-экономические показатели городских округов и муниципальных образований Республики Тыва. Статистический сборник. 2020:88). II кластер – 10 кожуунов: Каа-Хемский, Кызылский, Пий-Хемский, Тандинский, Тере-Холский, Тес-Хемский, Тоджинский, Чаа-Холский, Чеди-Холский, Эрзинский и г. Кызыл. Центру кластера соответствует точка с координатами (94,18; 50,98). Так как производство трудно организовать где-то в лесу, вдали от электрических, транспортных и прочих коммуникаций, мы округлили координаты полученной точки до точки расположения ближайшего населенного пункта – г. Кызыл. Суммарное поголовье овец и коз в полученном кластере составляет 432873 головы, что составляет 36 % от общего количества (Социально-экономические показатели городских округов и муниципальных образований Республики Тыва. Статистический сборник. 2020:82). Данный макрорайон объединил наиболее развитые промышленные районы республики. Полученные итоги расчетов представлены на рисунке 2. Как видно из рисунка, решение задачи кластеризации разделило районы РТ на этнокластеры, образованные по критерию близости к полученным центрам кластеров. Следует отметить, что из всех исходных точек (районных центров) имеется транспортное сообщение к полученным в результате расчетов точкам расположения центров кластеров.
Рисунок 2. Этноэкономические кластеры Республики Тыва При организации производства в трех и более точках в результате расчетов получено разбиение предприятий на зоны обслуживания, которое несколько снижает транспортные затраты, но увеличивает при этом затраты на эксплуатацию производственных помещений и общие затраты. Таким образом, в результате расчетов рассмотренный вариант с двумя кластерами является оптимальным. Заключение Самобытная культура тувинцев, сохранившаяся до сегодняшнего дня может стать одним из потенциальных точек роста экономики РТ. Однако формирование случайных очагов обрабатывающего производства, основанных на традиционных технологиях, в современных реалиях могут в основном удовлетворить внутренние потребности хозяйств, подвержены высокому риску и не всегда полученная продукция является конкурентоспособной. Учитывая традиционные виды хозяйствования коренного населения, географические особенности территории, целесообразно применение кластерного подхода и оптимизационных моделей к организации промышленного производства с применением современных технологий переработки продукции сельхозпроизводителей. Данный подход стимулирует дальнейшее развитие сельского хозяйства республики, развитие этнокластеров перерабатывающих производств, производства конкурентоспособной продукции с высокой добавленной стоимостью, а также сохранение уникальной культуры и традиций тувинского народа. С помощью предложенной математической модели получено подтверждение целесообразности решения правительства РТ об организации промышленных объектов в городах Кызыл и Чадаан и образования кластеров с центрами в соответствующих городах, которые являются точками пересечения автомобильных дорог нескольких районов. Это говорит о полезности разработанной модели и выбранного авторами алгоритма решения производственно-транспортной задачи. В качестве дальнейшего развития работы предполагается разработать полностью дискретную модель с булевыми переменными и матрицей реальных расстояний между пунктами по существующей системе дорог и провести сравнение результатов, полученных разными моделями на задачах не очень высокой размерности.
References
- 1. Alejnikov B.I. (1966). Zadacha optimal'nogo razmeshcheniya proizvodstva produkcii odnogo tipa // Ekonomika i matematicheskie metody. Vypusk 2. Tom 2. S. 272 – 282;Alibekov B.I. (1975). O zadache na razmeshchenie s ogranichennymi moshchnostyami // Ekonomika i matematicheskie metody. Vypusk 3. Tom 11. S. 534 – 541;Ahmetov, V.YA., Berdnikova, G.I., Salihova, Z.M. (2012). Etnoekonomika i ee rol' v ustojchivom razvitii sel'skih territorij Rossii // Ekonomika sel'skogo hozyajstva Rossii. №2. S. 78 – 86;Baisov I.M., Nikitina L.N., Bogdanov A.I. (2017). Optimizaciya mesta razmeshcheniya sklada torgovogo predpriyatiya // Vestnik SPGUTD. Seriya 1. Estestvennye i tekhnicheskie nauki. № 2. S. 91-93;Bogdanov A.I., Mongush B.S. (2018). Optimizaciya mesta raspolozheniya skladov s pomoshch'yu klasternogo analiza // Vestnik SPGUTD, Seriya 1. Estestvennye i tekhnicheskie nauki. № 4. S. 19 – 23;Bogdanov A.I., Mongush B.S. (2019). Matematicheskie modeli optimizacii proizvodstvenno-transportno-skladskih processov // Vestnik SPGUTD. Seriya 1. Estestvennye i tekhnicheskie nauki. № 1. S. 16-20;Bochkarev A.A. (2009). Teoriya i metodologiya processnogo podhoda k modelirovaniyu i integrirovannomu planirovaniyu cepi postavok: avtoref … dis. d.e.n. SPb. 39 s.;Gadzhinskij, A.M. (2012) Logistika. M.: Izdatel'sko – torgovaya korporaciya «Dashkov i Ko»;Granberg A.G. (1970). Mnogootraslevaya model' optimal'nogo razvitiya i razmeshcheniya proizvodstva v planovo-ekonomicheskih raschetah // Ekonomika i matematicheskie metody. Vyp. 3. T. 6. S. 393 – 406;Logistika. Integraciya i optimizaciya logisticheskih biznes- processov v cepyah postavok: Uchebnik MVA. (2014) / Sergeev V.I. (red.). Moskva: Eksmo;Klochko, E.N., Kobozeva, E.M. (2017). Etnoekonomika regiona: potencial, funkcii, bar'ery razvitiya // Biznes. Obrazovanie. Pravo. - №4. – S. 38 – 42;Madera, A.G. (2005) Opredelenie optimal'nogo razmeshcheniya logisticheskih moshchnostej // Integrirovannaya logistika. № 3. S. 12 – 15;Makarov A.G., Bogdanov A.I., Nikitina L.N., Mongush B.S. (2019). Integrirovannye modeli biznes-processov // Tekhnologiya tekstil'noj promyshlennosti. № 6 (384). S. 62-65;Modeli i metody teorii logistiki (2012). Lukinskij V.S. (red.). Sankt-Peterburg: Piter;Mongush B.S. (2019). Problemy resheniya integrirovannyh transportno - skladskih zadach // Regional'naya ekonomika: tekhnologii, ekonomika, ekologiya i infrastruktura: materialy III Mezhdunarodnoj nauchno – prakticheskoj konferencii (23-25 oktyabrya 2019g.). Kyzyl: TuvIKOPR SO RAN. S. 369-372;Procenko, O.D., Procenko, I.O. (2012). Logistika i upravlenie cepyami postavok – vzglyad v budushchee: makroekonomicheskij aspekt. M.: Izdatel'skij dom «Delo»;Sergeev, V.I. (2019). Logistika i upravlenie cepyami postavok: professiya XXI veka: analiticheskij obzor. Moskva: Izdatel'skij dom Vysshej shkoly ekonomiki;Hachaturov V.R. (1967). Algoritmy i programmy resheniya zadach razmeshcheniya predpriyatij s neogranichennymi ob"emami proizvodstva // Ekonomika i matem. metody. Vyp. 2. T. 3. S. 240-251;Jeremy F. Shapiro (2006). Modeling the supply chain. Boston: Cengage learning.
2. – Социально-экономические показатели городских округов и муниципальных образований Республики Тыва. 2021 г. Статистический сборник