Адаптивная регрессия для агент-ориентированного моделирования

Цыплаков Александр А.

doi:10.31857/S042473880028256-0

1. Введение

Традиционная теоретическая экономика, по сути, описывает «поведение неправдоподобно разумных людей в неправдоподобно простых ситуациях» (Leijonhufvud, 1993). Поведение обычных людей больше похоже на адаптивное, чем на полностью рациональное. Важность моделирования адаптивного поведения и адаптивного обучения давно осознана в макроэкономическом и финансовом моделировании (Leijonhufvud, 1993; Timmermann, 1993; Evans, Honkapohja, 2001; Carceles-Poveda, Giannitsarou, 2007; Sinitskaya, Tesfatsion, 2015). Предположение о том, что все агенты знают структуру экономического равновесия и действуют полностью оптимально на основе этого понимания, заменяется на более правдоподобное предположение, что агенты эконометрическими методами оценивают параметры своих внутренних моделей исходя из имеющихся данных. В частности, в современных исследованиях рассматриваются модели с обучением на основе (рекурсивного) метода наименьших квадратов, стохастического градиента и т.п. (Carceles-Poveda, Giannitsarou, 2007).

Очень актуальным использование адаптивного обучения является для агент-ориентированного моделирования. Агент-ориентированное моделирование — это распространившийся в последние годы подвид имитационного моделирования, помогающий изучению и прогнозированию явлений, происходящих в сложных экономических, социальных, биологических и других системах. Агент-ориентированные модели (АОМ) широко применяются в разных областях: дорожное движение (Nguyen et al., 2021), финансовые рынки (Iori, Porter, 2018), рынки электроэнергии (Weidlich, Veit, 2008), эпидемиология (Hunter, Namee, Kelleher, 2017), макроэкономика (Dawid H., Delli Gatti, 2018) и т.д.

В основе агентного подхода лежит индивидуальное поведение и взаимодействие агентов, входящих в изучаемую систему. Используемые в АОМ агенты — это компьютерные сущности внутри виртуальной системы — аналога моделируемой реальной системы, — которые производят некоторые действия и взаимодействуют с окружающей средой (в том числе с другими агентами). Агенты и содержащая их система имеют некоторые свойства (находятся в определенном состоянии). Агент может выбирать действия (из набора возможных) автономно от других агентов и от системы. Выбираемые действия приводят к изменению состояния системы во времени.

Как в любом имитационном моделировании, с АОМ проводятся вычислительные эксперименты в виде серии прогонов (испытаний)¹. Результаты по многим прогонам, содержащим случайность, можно обобщить, собрав и проанализировав статистику. Изменяя параметры, меняя сценарии экспериментов, можно делать прогнозы о поведении изучаемой системы в разных условиях.

1. Роберт Шеннон дал следующее определение имитационного моделирования: «Это процесс разработки компьютеризированной модели системы (или процесса) и проведения экспериментов с этой моделью с целью понимания поведения системы или же оценки различных стратегий для работы системы» (Shannon, 1976; Шеннон, 1978, с. 12).

Одной из важнейших характеристик агента в АОМ является то, что он может воспринимать окружающую обстановку и принимать решения на основе определенных правил и алгоритмов поведения. В частности, в основе поведения может лежать максимизация некоторой целевой функции, параметры которой адаптивно меняются в зависимости от окружающей обстановки.

С одной стороны, компьютерные агенты должны быть достаточно похожими по основным характеристикам поведения на свои реальные прототипы. С другой стороны, в АОМ при большом числе агентов не стоит использовать слишком сложные алгоритмы обучения, требующие запретительно больших затрат времени для проведения расчетов. Поэтому агенты в АОМ не должны получать слишком большой объем информации и не должны быть неправдоподобно разумными. Другими словами, агенты в АОМ, как правило, будут характеризоваться несовершенством информации и неполной рациональностью, а их поведение будет адаптивным и достаточно простым.

В агент-ориентированном моделировании опробованы разные алгоритмы, отвечающие за адаптивное поведение агентов (Brenner, 2006; Weidlich, Veit, 2008; DeAngelis, Diaz, 2019), например алгоритм Эрева–Рота, Q-обучение, обучающиеся системы классификаторов, генетические алгоритмы, нейронные сети, различные алгоритмы обучения с подкреплением и прочие методы машинного обучения. В (Rand, 2006) показано сходство общей идеи адаптивного поведения в АОМ и машинного обучения. Для агента в АОМ вся остальная модель представляет собой окружающую среду. Обучаясь, агент видоизменяет свою модель окружающего мира за счет поступающих извне информации и подкрепляющих вознаграждений.

Для простоты изложения метода пусть работа АОМ представляется в виде последовательности периодов $t = 1, \dots, T$ . У каждого агента $i = 1, \dots, N$ есть некоторая модель окружающего мира, где окружающий мир — это остальные агенты и содержащая агентов система. Это будет параметрическая модель, описываемая параметрами $a_{i t}$ . С точки зрения обучения агентов в течение каждого периода $t$ в АОМ происходит ряд событий (Rand, 2006):

каждый агент получает информацию об окружающем мире $y_{i t}$ , на ее основе он обновляет свою внутреннюю модель мира, корректируя параметры $a_{i t}$ ;
каждый агент решает на основе внутренней модели с параметрами $a_{i t}$ , какое действие $x_{i t}$ выбрать в текущем периоде;
каждый агент осуществляет выбранные действия $x_{i t}$ , что приводит к изменению состояний агентов и системы в целом.

Для реализации подобного рода адаптивного поведения в АОМ мы предлагаем использовать алгоритм, являющийся обобщением фильтра Калмана — SQ-фильтр. Первоначальная версия данного алгоритма была предложена для оценивания срочной структуры процентных ставок в статье (Авдеева, Цыплаков, 2015). В данной статье детально рассмотрена взаимосвязь SQ-фильтра с общей моделью пространства состояний. Показано, что SQ-фильтр можно рассматривать как приближенный алгоритм фильтрации, который эквивалентен полноценной процедуре фильтрации в случае гауссовской линейной модели пространства состояний.

Описанию модели пространства состояний и процедуры фильтрации для нее посвящен разд. 2. В разд. 3 описывается SQ-фильтр. В разд. 4 алгоритм конкретизирован для модели линейной регрессии с меняющимися параметрами, характеризующейся робастностью к выбросам. Предложена модификация алгоритма, делающая его более простым и удобным для прикладных вычислений. Наконец, в разд. 5 и 6 рассматривается использование такой адаптивной регрессии в двух экономических АОМ.

2. Модель пространства состояний

Процесс обучения агента в АОМ удобно представить в виде так называемой модели пространства состояний. Получаемая агентом информация отождествляется с наблюдаемым временным рядом $y_{t}$ . Используя эту информацию $y_{t}$ , агент адаптивно меняет параметры своей модели окружающего мира. Эти параметры с точки зрения модели пространства состояний представляют собой ненаблюдаемый вектор состояния $a_{t}$ . Связь вектора состояния $a_{t}$ с рядом $y_{t}$ описывается плотностью измерения, которую можно сформировать на основе внутренней модели окружающего мира агента. Процесс изменения во времени параметров $a_{t}$ описывается в виде плотности перехода.

Пусть $y_{1 : T} = (y_{1}, \dots, y_{T})$ — наблюдаемый (одномерный или многомерный) временной ряд. Типичное наблюдение $y_{t}$ представляет собой вектор $k \times 1$ . Модель для ряда $y$ сформулирована в терминах ряда состояний $a_{1 : T} = (a_{1}, \dots, a_{T})$ , где $a_{t}$ — вектор $m \times 1$ ненаблюдаемых компонент. Переменную $a_{t}$ называют переменной состояния.

Будем считать распределение $y_{1 : T}$ и $a_{1 : T}$ непрерывным. Совместная плотность $f (y_{1 : T}, a_{1 : T})$ в модели пространстве состояний строится из двух последовательностей условных плотностей (Tanizaki, 1996): плотность измерения $f (y_{t} | a_{1 : t}, y_{1 : t - 1}) = f (y_{t} | a_{t}, y_{1 : t - 1})$ , $t = 1, \dots, T$ ; плотность перехода $f (a_{t} | a_{1 : t - 1}, y_{1 : t - 1}) = f (a_{t} | a_{t - 1}, y_{1 : t - 1})$ , $t = 2, \dots, T$ . Начальную плотность $f (a_{1})$ можно рассматривать как частный случай плотности перехода при $t = 1$ .

Важной характеристикой модели пространства состояний является то, что плотность измерения не зависит от $a_{1 : t - 1}$ . Точно так же плотность перехода не зависит от $a_{1 : t - 2}$ , и, таким образом, модель имеет марковский характер условно относительно предыстории $y_{1 : t - 1}$ .

Процесс, который можно рассматривать как обучение, в модели пространства состояний называется фильтрацией. Фильтрация происходит рекуррентно с учетом информации, имеющейся к данному моменту времени $t$ ( $t = 1, \dots, T$ ), и представляет собой последовательность двух чередующихся шагов: шага прогнозирования и шага обновления.

Шаг прогнозирования. В момент $t - 1$ для наблюдаемого ряда известны значения $y_{1 : t - 1} = (y_{1}, \dots, y_{t - 1})$ . Это дает информацию о значении переменной состояния в период $t - 1$ (т.е. $a_{t - 1}$ ), что выражается плотностью $f (a_{t - 1} | y_{1 : t - 1})$ , которая берется с шага обновления периода $t - 1$ . Эту же информацию $y_{1 : t - 1}$ можно использовать для прогноза переменной состояния на следующий период $a_{t} :$

$f (a_{t} | y_{1 : t - 1}) = \int f (a_{t} | a_{t - 1}, y_{1 : t - 1}) f (a_{t - 1} | y_{1 : t - 1}) d a_{t - 1} ‍,$

прогноз наблюдаемого ряда на период $t$ в виде плотности —

$f (y_{t} | y_{1 : t - 1}) = \int f (y_{t} | a_{t}, y_{1 : t - 1}) f (a_{t} | y_{1 : t - 1}) d a_{t},$

где $f (a_{t} | a_{t - 1}, y_{1 : t - 1})$ и $f (y_{t} | a_{t}, y_{1 : t - 1})$ определяются моделью.

Шаг обновления. После того как в период $t$ поступит новое наблюдение $y_{t}$ , можно скорректировать оценку состояния системы на основе $y_{1 : t} = (y_{1}, \dots, y_{t})$ :

$f (a_{t} | y_{1 : t}) = f (y_{t} | a_{t}, y_{1 : t - 1}) f (a_{t} | y_{1 : t - 1}) / f (y_{t} | y_{1 : t - 1}) .$

Описанная общая модель пространства состояний не очень пригодна для проведения прикладных расчетов, так как в общем случае алгоритм фильтрации содержит многомерные интегралы. Однако в частном случае — гауссовской линейной модели пространства состояний — прямое использование интегралов можно заменить более простым алгоритмом с матричными вычислениями. В такой модели совместное распределение $y_{1 : T}$ и $a_{1 : T}$ является многомерным нормальным и плотность измерения примет вид — $f (y_{t} | a_{1 : t}, y_{1 : t - 1}) = f (y_{t} | a_{t}, y_{1 : t - 1}) = = φ (y_{t} - R_{y t} - R_{y a t} a_{t}, Ω_{y t}),$ а плотность перехода — $f (a_{t} | a_{1 : t - 1}, y_{1 : t - 1}) = f (a_{t} | a_{t - 1}, y_{1 : t - 1}) = = φ (a_{t} - R_{a t} - R_{a a t} a_{t - 1}, Ω_{a t}),$ где $R_{y t}$ ( $k \times 1$ ), $R_{y a t}$ ( $k \times m$ ), $Ω_{y t}$ ( $k \times k$ ), $R_{a t}$ ( $m \times 1$ ), $R_{a a t}$ ( $m \times m$ ), $Ω_{a t}$ ( $m \times m$ ) — матрицы параметров модели, а через $φ (x, Σ)$ обозначена функция плотности многомерного нормального распределения $N (0, Σ)$ . Для n-мерного распределения

$φ (x, Σ) = {(\sqrt{{(2 π)}^{n} |Σ|})}^{- 1} e x p (- 0,5 x^{T} Σ^{- 1} x) .$

Плотности, получаемые на шаге предсказания и шаге обновления гауссовской линейной модели, тоже многомерные нормальные:

$f (a_{t - 1} | y_{1 : t - 1}) = φ (a_{t - 1} - {\bar{a}}_{t - 1}, {\bar{P}}_{t - 1}), f (a_{t} | y_{1 : t - 1}) = φ (a_{t} - {\tilde{a}}_{t}, {\tilde{P}}_{t}) .$

Шаг предсказания дает плотность

$f (a_{t} | y_{1 : t - 1}) = \int φ (a_{t} - R_{a t} - R_{a a t} a_{t - 1}, Ω_{a t}) φ (a_{t - 1} - {\bar{a}}_{t - 1}, {\bar{P}}_{t - 1}) d a_{t - 1} ‍ .$

Для функции плотности многомерного нормального распределения $φ (\cdot)$ выполнено

$\int φ (x - μ, Σ) φ (y - A x, Ω) d x ‍ = φ (y - A μ, A Σ A^{T} + Ω) .$

Поэтому $f (a_{t} | y_{1 : t - 1}) = φ (a_{t} - {\tilde{a}}_{t}, {\tilde{P}}_{t}),$ где ${\tilde{P}}_{t} = R_{a a t} {\bar{P}}_{t - 1} R_{a a t}^{T} + Ω_{a t}, {\tilde{a}}_{t} = R_{a t} + R_{a a t} {\bar{a}}_{t - 1} .$

Шаг обновления дает плотность

$f (a_{t} | y_{1 : t}) = \frac{φ (y_{t} - R_{y t} - R_{y a t} a_{t}, Ω_{y t}) φ (a_{t} - {\tilde{a}}_{t}, {\tilde{P}}_{t})}{\int φ (y_{t} - R_{y t} - R_{y a t} a_{t}, Ω_{y t}) φ (a_{t} - {\tilde{a}}_{t}, {\tilde{P}}_{t}) d a_{t}} .$

Для функции плотности многомерного нормального распределения $φ (\cdot)$ выполнено

$\frac{φ (x - μ, Σ) φ (y - A x, Ω)}{\int φ (x - μ, Σ) φ (y - A x, Ω) d x} = φ (x - μ - \tilde{Σ} A^{T} Ω^{- 1} (y - A μ), \tilde{Σ}),$ $\tilde{Σ} = {(Σ^{- 1} + A^{T} Ω^{- 1} A)}^{- 1} .$

Поэтому

$f (a_{t} | y_{1 : t}) = φ (a_{t} - {\bar{a}}_{t}, {\bar{P}}_{t}),$ ${\bar{P}}_{t} = {(R_{y a t}^{T} Ω_{y t}^{- 1} R_{y a t} + {\tilde{P}}_{t}^{- 1})}^{- 1}, {\bar{a}}_{t} = {\tilde{a}}_{t} + {\bar{P}}_{t} R_{y a t}^{T} Ω_{y t}^{- 1} (y_{t} - R_{y t} - R_{y a t} {\tilde{a}}_{t}) .$ Таким образом, в гауссовской линейной модели шаг предсказания задается формулами ${\tilde{P}}_{t} = R_{a a t} {\bar{P}}_{t - 1} R_{a a t}^{T} + Ω_{a t},$ ${\tilde{a}}_{t} = R_{a t} + R_{a a t} {\bar{a}}_{t - 1},$ а шаг обновления — ${\bar{P}}_{t} = {({\tilde{P}}_{t}^{- 1} + {\tilde{N}}_{t})}^{- 1}, {\bar{a}}_{t} = {\tilde{a}}_{t} + {\bar{P}}_{t} {\tilde{s}}_{t},$ где мы обозначили ${\tilde{N}}_{t} = R_{y a t} Ω_{y t}^{- 1} R_{y a t}, {\tilde{s}}_{t} = R_{y a t}^{T} Ω_{y t}^{- 1} (y_{t} - R_{y t} - R_{y a t} a_{t}) .$

Эти рекуррентные формулы для ${\tilde{a}}_{t}$ , ${\tilde{P}}_{t}$ , ${\bar{P}}_{t}$ , ${\bar{a}}_{t}$ соответствуют классическому алгоритму фильтрации — фильтру Калмана (в одной из его возможных записей) (см., например, (Tanizaki, 1996)). Рекурсия начинается с ${\tilde{P}}_{1} = Ω_{a 1}, {\tilde{a}}_{1} = R_{a 1} .$

3. SQ-фильтр

Общие формулы фильтрации, записанные через многомерные интегралы, позволяют работать с произвольными моделями, но пользоваться ими напрямую слишком трудно. Фильтр Калмана — это удобный и несложный алгоритм для моделирования обучения агента², но он позволяет работать только с очень ограниченным кругом моделей окружающего мира. Это связано с условием, что у наблюдаемой переменной $y_{t}$ нормальное условное распределение вида $y_{t} | a_{t}, y_{1 : t - 1} \sim N (R_{y t} + R_{y a t} a_{t}, Ω_{y t}),$ у которого математическое ожидание линейно по параметрам $a_{t}$ , а значение ковариационной матрицы $Ω_{y t}$ точно известно заранее. Наша цель состоит в том, чтобы предложить более общий алгоритм, который был бы таким же простым, как фильтр Калмана, но позволял работать с более широким спектром моделей окружающего мира.

2. Насколько можно судить, до настоящего времени не только модели временных рядов семейств GAS (Creal, Koopman, Lucas, 2013) и DSC (Harvey, 2013), но и классический фильтр Калмана не использовались для моделирования обучения агентов в АОМ.

В гауссовском линейном случае плотность измерения равна $f (y_{t} | a_{t}, y_{1 : t - 1}) = φ (y_{t} - R_{y t} - R_{y a t} a_{t}, Ω_{y t})$ . Будем рассматривать эту плотность как функцию правдоподобия, считая $y_{t}$ наблюдением, а $a_{t}$ — неизвестным параметром. Это не функция правдоподобия в обычном смысле, но в теории метода максимального правдоподобия (ММП) есть несколько понятий и результатов, которые нам здесь понадобятся.

Логарифмическая функция правдоподобия равна

$λ_{t} (a_{t}) = - 0,5 k l n (2 π) - 0,5 l n |Ω_{y t}| - 0,5 {(y_{t} - R_{y t} - R_{y a t} a_{t})}^{T} Ω_{y t}^{- 1} (y_{t} - R_{y t} - R_{y a t} a_{t}) .$

При фиксированном $y_{t}$ это функция от $a_{t}$ . Направление увеличения функции $λ_{t}$ задается ее градиентом $\nabla λ_{t} (a_{t}) = R_{y a t}^{T} Ω_{y t}^{- 1} (y_{t} - R_{y t} - R_{y a t} a_{t}) .$ В ММП этот градиент называется скор-вектором (score). Также важна матрица вторых производных $λ_{t}$ (матрица Гессе): $\nabla^{2} λ_{t} ({\tilde{a}}_{t}) = - R_{y a t}^{T} Ω_{y t}^{- 1} R_{y a t} .$ Эти функции связаны с величинами ${\tilde{s}}_{t}$ и ${\tilde{N}}_{t}$ , которые мы определили выше и которые входят в формулы шага обновления фильтра Калмана:

${\tilde{s}}_{t} = \nabla λ_{t} ({\tilde{a}}_{t}) = R_{y a t}^{T} Ω_{y t}^{- 1} (y_{t} - R_{y t} - R_{y a t} {\tilde{a}}_{t}),$ ${\tilde{N}}_{t} = - \nabla^{2} λ_{t} ({\tilde{a}}_{t}) = R_{y a t}^{T} Ω_{y t}^{- 1} R_{y a t} .$

С точки зрения теории ММП, если $λ_{t} (a_{t})$ — логарифмическая функция правдоподобия, то математическое ожидание ее градиента (скор-вектора) $\nabla λ_{t} (a_{t})$ , рассчитанное по плотности $f (y_{t} | a_{t}, y_{1 : t - 1}) = e x p (λ_{t} (a_{t})),$ равно нулю, а ковариационная матрица градиента $\nabla λ_{t} (a_{t})$ — это так называемая информационная матрица. Чтобы отразить, что $λ_{t} (a_{t})$ зависит от $y_{t},$ будем использовать более полную запись $λ_{t} (a_{t}; y_{t})$ . В случае линейного гауссовского наблюдения информационная матрица равна

$\begin{matrix} \int \nabla λ_{t} (a_{t}; y_{t}) \nabla λ_{t}^{T} (a_{t}; y_{t}) φ (y_{t} - R_{y t} - R_{y a t} a_{t}, Ω_{y t}) d y_{t} = \\ = \int R_{y a t}^{T} Ω_{y t}^{- 1} (y_{t} - R_{y t} - R_{y a t} a_{t}) {(y_{t} - R_{y t} - R_{y a t} a_{t})}^{T} Ω_{y t}^{- 1} R_{y a t} φ (y_{t} - R_{y t} - R_{y a t} a_{t}, Ω_{y t}) d y_{t} = \\ = R_{y a t}^{T} Ω_{y t}^{- 1} \int z z^{T} φ (z, Ω_{y t}) d z Ω_{y t}^{- 1} R_{y a t} = R_{y a t}^{T} Ω_{y t}^{- 1} Ω_{y t} Ω_{y t}^{- 1} R_{y a t} = R_{y a t}^{T} Ω_{y t}^{- 1} R_{y a t} . \end{matrix}$

(Мы воспользовались тем, что ковариационная матрица многомерного нормального распределения с плотностью $φ (z, Ω_{y t})$ — это $Ω_{y t}$ .) Таким образом, информационная матрица здесь совпадает с величиной ${\tilde{N}}_{t}$ .

Известный прикладной алгоритм фильтрации в случае нелинейных функций измерения и перехода — это так называемый расширенный фильтр Калмана, основанный на линеаризации нелинейных функций (см., например, (Tanizaki, 1996)). Мы воспользуемся приближенным алгоритмом, основанным на другом принципе — SQ-фильтром³. В нем вместо истинного логарифма плотности наблюдения $λ_{t} (a_{t}; y_{t}) = l n f (y_{t} | a_{t}, y_{1 : t - 1})$ используется квадратичная по переменной состояния $a_{t}$ функция

3. State-quadratic — квадратичный по состоянию.

$λ_{t} ({\tilde{a}}_{t}; y_{t}) + {\tilde{s}}_{t}^{T} (a_{t} - {\tilde{a}}_{t}) - 0,5 {(a_{t} - {\tilde{a}}_{t})}^{T} {\tilde{N}}_{t} (a_{t} - {\tilde{a}}_{t}),$

где ${\tilde{s}}_{t}$ и ${\tilde{N}}_{t}$ — это соответствующие градиент и информационная матрица: ${\tilde{s}}_{t} = \nabla λ_{t} ({\tilde{a}}_{t}; y_{t}), {\tilde{N}}_{t} = \int \nabla λ_{t} ({\tilde{a}}_{t}; y_{t}) \nabla λ_{t}^{T} ({\tilde{a}}_{t}; y_{t}) e x p (λ_{t} ({\tilde{a}}_{t}; y_{t})) d y_{t} .$ При $a_{t} = {\tilde{a}}_{t}$ приближение совпадает с $λ_{t} (a_{t}; y_{t})$ по значению и первым производным. В общем случае вторые производные могут не совпадать, но $- {\tilde{N}}_{t}$ по известному информационному тождеству ММП — это математическое ожидание матрицы вторых производных $λ_{t} (a_{t}; y_{t})$ , рассчитанное по плотности $e x p (λ_{t} ({\tilde{a}}_{t}; y_{t}))$ : ${\tilde{N}}_{t} = - \int \nabla^{2} λ_{t} ({\tilde{a}}_{t}; y_{t}) e x p (λ_{t} ({\tilde{a}}_{t}; y_{t})) d y_{t} .$

Используя на шаге обновления вместо $φ (y_{t} - R_{y t} - R_{y a t} a_{t}, Ω_{y t})$ экспоненту указанного приближения, мы получаем те же рекуррентные формулы фильтрации, что и ранее для гауссовской линейной модели пространства состояний.

Рассмотренный алгоритм был первоначально предложен в статье (Авдеева, Цыплаков, 2015) для оценивания срочной структуры процентных ставок. Наиболее близкие аналоги описанного алгоритма — это модели временных рядов семейств GAS (Creal, Koopman, Lucas, 2013) и DSC (Harvey, 2013), также он напоминает семейство методов экспоненциального сглаживания (Hyndman et al., 2008; Лукашин, 2003) и метод стохастического градиента (Carceles-Poveda, Giannitsarou, 2007).

SQ-фильтр обладает рядом преимуществ по сравнению с указанными альтернативными методами. Методы экспоненциального сглаживания, стохастического градиента и метод калмановской фильтрации подходят только для очень узких классов переменных $y_{t}$ . Например, они не подходят для качественных переменных $y_{t}$ , имеющих дискретное распределение.

В этом смысле методы GAS и DSC более универсальные, поскольку основаны на скор-векторе произвольного распределения наблюдаемой переменной. SQ-фильтр можно рассматривать как их частный случай. Важным преимуществом SQ-фильтра по сравнению с GAS и DSC является то, что этот метод конкретизирует, как именно входит скор-вектор в рекурсии для меняющихся параметров. Например, если плотность наблюдения будет линейной гауссовской, то SQ-фильтр сведется к фильтру Калмана, который, как известно, обладает оптимальными свойствами. Методы GAS и DSC не дают здесь конкретных рекомендаций — на их основе можно сформулировать очень много разных алгоритмов, в том числе далеких от оптимальности.

SQ-фильтр позволяет руководствоваться при формулировке алгоритма обучения агента четкой процедурой. Сначала из содержательных соображений формулируется внутренняя модель окружающего мира для агента. Далее на основе данной модели формулируется вероятностная параметрическая модель для наблюдаемой переменной $y_{t}$ . Это дает плотность измерения $e x p (λ_{t} (a_{t}))$ и скор-вектор $\nabla λ_{t}^{T} (a_{t})$ . По плотности измерения аналитическим интегрированием вычисляется информационная матрица ${\tilde{N}}_{t}$ . Скор-вектор и информационная матрица используются в формулах SQ-фильтра для обучения агента.

К недостаткам SQ-фильтра можно отнести то, что для получения матрицы ${\tilde{N}}_{t}$ требуется интегрирование. В то же время для многих достаточно важных и полезных случаев интегрирование может быть произведено аналитически, что служит важным преимуществом SQ-фильтра по сравнению с фильтрацией в общей модели пространства состояний.

То что SQ-фильтр в общем случае является только приближением для точной фильтрации, не является принципиальным недостатком, поскольку правдоподобность и простота поведения агента более важны, чем полная оптимальность его поведения.

Один из самых удобных типов моделей окружающего мира для алгоритмов обучения — это линейные модели регрессии, поэтому конкретизируем описанный общий SQ-фильтр для случая регрессии с меняющимися параметрами. Для регрессионной ошибки выберем семейство распределений с толстыми хвостами. Это один из случаев, когда информационную матрицу для SQ-фильтра можно вычислить аналитически.

4. SQ-фильтр для регрессии с меняющимися параметрами

Рассмотрим линейную регрессионную модель общего вида $y_{t} = X_{t} β_{t} + ε_{t}$ , где $y_{t}$ — моделируемая переменная, $X_{t}$ — вектор-строка объясняющих переменных длины $m - 1$ (обычно содержит единицу, отвечающую за константу). Переменные $X_{t}$ для простоты будем считать фиксированными (хотя случайные регрессоры и лаги ряда $y_{t}$ не представляют проблемы). Пусть коэффициенты регрессии $β_{t}$ $((m - 1) \times 1)$ и дисперсия ошибки $v a r (ε_{t}) = e^{h_{t}}$ меняются во времени. Дисперсия зависит от показателя волатильности $h_{t}$ . Предположим, что динамика меняющихся параметров $a_{t} = {(β_{t} h_{t})}^{T}$ задается линейным гауссовским процессом марковского вида с плотностью перехода $f (a_{t} | a_{1 : t - 1}, y_{1 : t - 1}) = φ (a_{t} - a_{t - 1}, Ω_{a t}),$ где ковариационная матрица блочно-диагональная:

$Ω_{a t} = Ω_{a t} = (\begin{array}{l} Ω_{β t} & 0_{m - 1} \\ 0_{m - 1}^{T} & ω_{h t} \end{array}) = d i a g (Ω_{β t}, ω_{h t}) .$

В использованных ранее обозначениях $R_{a t} = 0_{m},$ $R_{a a t} = I_{m}$ .

Введем нормированную ошибку регрессии $ξ_{t} = e^{- h_{t} / 2} ε_{t},$ т.е. ошибку с нулевым математическим ожиданием и нулевой дисперсией. При этом $y_{t} = X_{t} β_{t} + e^{h_{t} / 2} ξ_{t} .$

Для достижения робастности (устойчивости) регрессии к возможным выбросам (резко выделяющимся значениям) предположим, что $ξ_{t}$ имеет t-распределение Стьюдента⁴ с $κ$ степенями свободы, нормированное к единичной дисперсии, так что

4. Об использовании t-распределения в статистическом моделировании (Lange, Little, Taylor, 1989).

${\sqrt{\frac{κ}{κ - 2}} ξ_{t}|}_{a_{1 : t}, y_{1 : t - 1}} \sim S t_{κ},$

где $S t_{κ}$ — обычное t-распределение с плотностью

$f_{S t, κ} (T) = [Γ (\frac{κ + 1}{2}) / \sqrt{κ π} Γ (\frac{κ}{2})] {(1 + \frac{T^{2}}{κ})}^{- (κ + 1) / 2} .$

Здесь мы учли, что дисперсия t-распределения равна $κ / (κ - 2)$ . С учетом масштабирования плотность измерения в данном случае имеет вид

$f (y_{t} | a_{1 : t}, y_{1 : t - 1}) = f_{S t, κ} (\sqrt{\frac{κ}{κ - 2}} e^{- h_{t} / 2} (y_{t} - X_{t} β_{t})) \sqrt{\frac{κ}{κ - 2}} e^{- h_{t} / 2} .$

Указанные плотности перехода и измерения задают модель регрессии с меняющимися параметрами. Найдем для данной модели SQ-фильтр. Соответствующая логарифмическая функция правдоподобия измерения равна

$λ_{t} = λ_{t} (a_{t}) = l n f_{S t, κ} (\sqrt{\frac{κ}{κ - 2}} ξ_{t}) + 0,5 l n (\frac{κ}{κ - 2}) - 0,5 h_{t},$

где $ξ_{t} = ξ_{t} (a_{t}) = e^{- h_{t} / 2} (y_{t} - X_{t} β_{t})$ , или

$λ_{t} = l n Γ (0,5 (κ + 1)) - l n Γ (0,5 κ) - 0,5 l n (π (κ - 2)) - 0,5 (κ + 1) l n (1 + ξ_{t}^{2} / (κ - 2)) - 0,5 h_{t} .$

Градиент функции $λ_{t}$ равен

$\nabla λ_{t} = (\begin{array}{l} [(κ + 1) ξ_{t} / (κ - 2 + ξ_{t}^{2})] e^{- h_{t} / 2} X_{t}^{T} \\ 0,5 (κ ξ_{t}^{2} - κ + 2) / (κ - 2 + ξ_{t}^{2}) \end{array}) .$

Вектор ${\tilde{s}}_{t}$ получим, подставив в данную формулу ${\tilde{h}}_{t}$ вместо $h_{t}$ и ${\tilde{ξ}}_{t} = e^{- {\tilde{h}}_{t} / 2} (y_{t} - X_{t} {\tilde{β}}_{t})$ вместо $ξ_{t}$ .

Информационную матрицу измерения ${\tilde{N}}_{t}$ найдем как ковариационную матрицу $\nabla λ_{t}$ с учетом того, что $ξ_{t} \sqrt{κ / (κ - 2)}$ имеет распределение Стьюдента, а ${ξ_{t}}^{2} \sqrt{κ / (κ - 2)}$ — распределение Фишера со степенями свободы 1 и $κ$ . Имеется известная связь между распределением Фишера и бета-распределением, из которой следует что $ξ_{t}^{2} / (κ - 2 + ξ_{t}^{2}) \sim B_{1 / 2, κ / 2},$ где $B_{1 / 2, κ / 2}$ — бета-распределение с параметрами $1 / 2$ и $κ / 2$ .

Поскольку $ξ_{t}$ имеет симметричное распределение, матрица ${\tilde{N}}_{t}$ будет блочно-диагональной. Используя формулы моментов бета-распределения, получим

${\tilde{N}}_{t} = (\begin{array}{l} \frac{κ (κ + 1)}{(κ - 2) (κ + 3)} e^{- {\tilde{h}}_{t}} X_{t}^{T} X_{t} & 0 \\ 0^{T} & κ / (2 κ + 6) \end{array}) .$

Предположим, что матрица ${\tilde{P}}_{1} = Ω_{a 1}$ является блочно-диагональной. Это свойство будет сохраняться для матриц ${\tilde{P}}_{t}$ и ${\bar{P}}_{t}$ на дальнейших шагах SQ-фильтра. Введем соответствующие обозначения для диагональных блоков ${\tilde{P}}_{t} = d i a g ({\tilde{P}}_{β t}, {\tilde{p}}_{h t}),$ ${\bar{P}}_{t} = d i a g ({\bar{P}}_{β t}, {\bar{p}}_{h t}) .$

Тогда уравнения SQ-фильтра можно разделить на уравнения для коэффициентов $β$ и для волатильности $h$ :

${\tilde{P}}_{β t} = {\bar{P}}_{β, t - 1} + Ω_{β t}, {\tilde{p}}_{h t} = {\bar{p}}_{h, t - 1} + ω_{h t},$ ${\tilde{β}}_{t} = {\bar{β}}_{t - 1}, {\tilde{h}}_{t} = {\bar{h}}_{t - 1},$

${\bar{P}}_{β t} = {({\tilde{P}}_{β t}^{- 1} + \frac{κ (κ + 1)}{(κ - 2) (κ + 3)} e^{- {\tilde{h}}_{t}} X_{t}^{T} X_{t})}^{- 1}, {\bar{p}}_{h t} = {({\tilde{p}}_{h t}^{- 1} + \frac{κ}{2 κ + 6})}^{- 1},$

${\bar{β}}_{t} = {\tilde{β}}_{t} + \frac{(κ + 1) {\tilde{ξ}}_{t}}{κ - 2 + {\tilde{ξ}}_{t}^{2}} e^{- {\tilde{h}}_{t} / 2} {\bar{P}}_{β t} X_{t}^{T}, {\bar{h}}_{t} = {\tilde{h}}_{t} + 0,5 {\bar{p}}_{h t} \frac{κ {\tilde{ξ}}_{t}^{2} - κ + 2}{κ - 2 + {\tilde{ξ}}_{t}^{2}} .$

Произведем с этими уравнениями следующие преобразования. Во-первых, уберем волну над переменными, чтобы разгрузить обозначения. Во-вторых, заметим, что по свойствам матричных операций имеем ${\bar{P}}_{β t} = P_{β t} - P_{β t} X_{t}^{T} c_{t}^{- 2} X_{t} P_{β t},$ $e^{- h_{t} / 2} {\bar{P}}_{β t} X_{t}^{T} = \frac{(κ - 2) (κ + 3)}{κ (κ + 1)} c_{t}^{- 2} e^{h_{t} / 2} P_{β t} X_{t}^{T},$ где $c_{t} = \sqrt{\frac{(κ - 2) (κ + 3)}{κ (κ + 1)} e^{h_{t}} + X_{t} P_{β t} X_{t}^{T}} .$ В-третьих, исключим из уравнений ${\bar{P}}_{β t}$ , ${\bar{β}}_{t}$ и ${\bar{h}}_{t}$ (предсказание для нас важнее, чем обновление). Тем самым мы получили уравнения⁵:

5. Заметим, что несложно распространить данный фильтр на случай нелинейной регрессии вида yt=ψtβt+εt . В приведенных формулах Xt заменяется на градиент ∇ψtT . Пример см. в (Авдеева, Цыплаков, 2015).

$ξ_{t} = e^{- h_{t} / 2} (y_{t} - X_{t} β_{t}),$ $β_{t + 1} = β_{t} + \frac{(κ - 2) (κ + 3) ξ_{t}}{κ (κ - 2 + ξ_{t}^{2})} e^{h_{t} / 2} c_{t}^{- 2} P_{β t} X_{t}^{T},$

$P_{β, t + 1} = P_{β t} - P_{β t} X_{t}^{T} c_{t}^{- 2} X_{t} P_{β t} + Ω_{β, t + 1}, h_{t + 1} = h_{t} + 0,5 {\bar{p}}_{h t} (κ ξ_{t}^{2} - κ + 2) / (κ - 2 + ξ_{t}^{2}) .$

${\bar{p}}_{h, t + 1} = {({({\bar{p}}_{h t} + ω_{h, t + 1})}^{- 1} + κ / (2 κ + 6))}^{- 1} .$

Технические подробности численной реализации данного алгоритма приведены в Приложении.

Если $ω_{h, t + 1} = ω_{h}$ — константа, то последовательность ${\bar{p}}_{h t}$ будет сходящейся. Таким образом, на практике можно упростить рекурсию для $h_{t}$ , исключив из алгоритма ${\bar{p}}_{h t}$ :

$h_{t + 1} = h_{t} + ρ (κ ξ_{t}^{2} - κ + 2) / (κ - 2 + ξ_{t}^{2}),$

где $ρ$ — половина соответствующего предела, коэффициент сглаживания.

Робастность фильтра к выбросам связана с тем, что квадрат $ξ_{t}$ в знаменателе в рекурсиях для $β_{t}$ и $h_{t}$ приглушает влияние больших по модулю значений $ξ_{t}$ , причем это проявляется в наибольшей степени при малых значениях параметра степеней свободы $κ$ . В пределе при больших $κ$ (при приближении распределения ошибок регрессии к нормальному) такая робастность теряется.

5. Обучение по адаптивной регрессии в модели искусственного фондового рынка

Модель была разработана в Институте Санта-Фе (Нью-Мексико, США) в конце 1980 – начале 1990-х годов. При описании модели мы будем опираться на статью (Arthur et al., 1997)⁶. Реализация несколько модифицированной модели на языке Objective-C в рамках агент-ориентированного инструментария Swarm имеется в свободном доступе⁷.

6. Другую литературу по этой модели можно найти на посвященной этой теме странице Л. Тесфатсион (Tesfatsion, 2012).

7. См. >>>>

Модель действует в дискретном времени ( $t = 1, \dots, T$ ). На рынке идет торговля только одним видом акций с экзогенно определяемыми случайными дивидендами $d_{t}$ . Имеется также безрисковый актив с однопериодной ставкой $r_{f}$ . Участниками фондового рынка являются «трейдеры» и «специалист» (аукционист). Трейдеры $(i = 1, \dots, N)$ могут покупать и продавать акции (выбирать $x_{t i}$ ). При этом можно открывать короткую позицию и брать в долг по ставке $r_{f}$ . Акции безгранично делимы. Всего имеется $N$ акций (по числу трейдеров). Каждый период трейдер распределяет имеющееся у него богатство между деньгами и акциями.

Если в момент $t$ трейдер $i$ обладает богатством $w_{i t}$ , цена акции равна $p_{t}$ и он включает в свой портфель $x_{i t}$ акций, то в безрисковый актив будет вложена сумма $w_{i t} - p_{t} x_{i t}$ . В период $t + 1$ вложения в акции дадут дивиденды $d_{t + 1}$ . Также можно будет продать акции по цене $p_{t + 1}$ , а вложения в безрисковый актив дадут проценты по ставке $r_{f}$ . Таким образом, в период $t + 1$ трейдер будет обладать богатством $w_{i, t + 1} = (p_{t + 1} + d_{t + 1}) x_{i t} + (1 + r_{f}) (w_{i t} - p_{t} x_{i t}) .$

Предполагается, что при составлении портфеля (выборе $x_{i t}$ ) трейдер максимизирует ожидаемую полезность от богатства в следующем периоде исходя из той информации, которой обладает на момент $t$ , т.е. он максимизирует величину $E_{i t} (u (w_{i, t + 1}))$ по $x_{i t},$ где $E_{i t}$ — условное математическое ожидание, соответствующее представлениям инвестора в момент $t$ о распределении $p_{t + 1} + d_{t + 1}$ , а $u (\cdot)$ — функция полезности.

Предполагается, что в соответствии с представлениями трейдера величина $p_{t + 1} + d_{t + 1}$ имеет нормальное условное распределение с математическим ожиданием $E_{i t} (p_{t + 1} + d_{t + 1})$ и дисперсией $v a r_{i t} [p_{t + 1} + d_{t + 1}]$ , а функция полезности трейдера $u (w)$ относится к семейству функций CARA (constant absolute risk aversion — с постоянным абсолютным неприятием риска), т.е. $u (w) = - e x p (- λ w) .$

Трейдеры в модели идентичны по функции полезности и алгоритму поведения, но каждый из них имеет свои ожидания и использует их для формирования спроса. При указанных предположениях оптимальное решение $x_{i t}$ зависит от двух первых условных моментов величины $p_{t + 1} + d_{t + 1}$ по формуле $x_{i t} = (E_{i t} (p_{t + 1} + d_{t + 1}) - (1 + r_{f}) p_{t}) / (λ v a r_{i t} [p_{t + 1} + d_{t + 1}]) .$

При сделанных предположениях спрос на акции устроен так, что не зависит от богатства. Это позволяет оставить изменение богатства трейдеров за рамками модели.

В течение каждого периода $t$ происходит следующая последовательность событий:

в начале периода генерируется очередной дивиденд $d_{t}$ по модели авторегрессии первого порядка $d_{t} = \bar{d} + φ (d_{t - 1} - \bar{d}) + ε_{t},$ где независимая ошибка имеет нормальное распределение $ε_{t} \sim N (0, σ_{ε}^{2})$ ;
трейдеры используют $d_{t}$ , а также предысторию дивидендов и цен ( $p_{t - 1}, d_{t - 1}, \dots$ ), чтобы сформировать прогноз для суммы дивидендов и цены в следующем периоде, т.е. для величины $p_{t + 1} + d_{t + 1}$ . Прогноз — это формула точечного прогноза $E_{t i} = E_{t i} (p_{t})$ и измеритель точности этого прогноза $σ_{t i}^{2};$
далее каждый трейдер рассчитывает свою функцию спроса $x_{t i} (p_{t})$ . При этом он использует $E_{t i} (p_{t})$ в качестве $E_{t i} (p_{t + 1} + d_{t + 1})$ и $σ_{t i}^{2}$ в качестве $v a r_{t i} [p_{t + 1} + d_{t + 1}]$ , так что его спрос оказывается равным $x_{t i} = (E_{t i} (p_{t}) - (1 + r_{f}) p_{t}) / λ σ_{t i}^{2};$
трейдеры сообщают свои функции спроса $x_{t i} (p)$ специалисту, который вычисляет равновесную цену $p_{t}$ , удовлетворяющую уравнению $\sum_{i = 1}^{n} x_{t i} (p_{t}) = N .$ Это будет цена на акции в период $t;$
каждый трейдер реализует имеющиеся у него акции $x_{i, t - 1}$ по цене $p_{t}$ , а затем включает в свой портфель $x_{t i} = x_{t i} (p_{t})$ акций;
происходит обновление параметров прогнозных алгоритмов трейдеров, так как прогнозы предыдущего периода теперь можно сравнить с фактически реализовавшейся величиной $p_{t} + d_{t}$ .

По условиям модели прогноз линеен по $p_{t} + d_{t}$ : $E_{t i} (p_{t}) = a_{t i} (p_{t} + d_{t}) + b_{t i},$ и прогнозы трейдеры формируют путем обучения. В исходной модели у каждого трейдера есть набор из $M$ предикторов, с помощью которых вычисляются $E_{t i} (p_{t})$ , $σ_{t i}^{2}$ . Предикторы работают по принципу обучающейся системы классификаторов (learning classifier system). Выбор предиктора и его видоизменение определяются генетическими алгоритмами, показатель точности меняется по формуле простого экспоненциального сглаживания. Подробности алгоритмов обучения исходной модели мы здесь не рассматриваем (Arthur et al., 1997).

Работа модели определяется рядом параметров, которые перечислены в табл. 1.

Таблица 1. Базовая конфигурация модели искусственного фондового рынка

Атрибут модели	Значение
Число агентов (трейдеров) N	25
Количество акций N	Совпадает с числом агентов
Средний дивиденд $\bar{d}$	10
Коэффициент авторегрессии для дивидендов $φ$	0,95
Дисперсия ошибки для дивидендов $σ_{ε}^{2}$	0,0743
Безрисковая ставка за период $r_{f}$	0,1
Коэффициент функции полезности CARA $λ$	0,5

Заметим, что у рассматриваемой агент-ориентированной модели искусственного фондового рынка имеется теоретический аналог — однородное равновесие с рациональными ожиданиями (Arthur et al., 1997). В этом равновесии цена $p_{t}^{R E E}$ линейно связана с дивидендами $p_{t} = p_{t}^{R E E} = f d_{t} + g,$ где $f = φ / (1 + r_{f} - φ), g = (1 + f) {(r_{f})}^{- 1} ((1 - φ) \bar{d} - λ (1 + f) σ_{ε}^{2}) .$

Прогноз $p_{t + 1} + d_{t + 1}$ как функция $p_{t} + d_{t}$ имеет вид $E_{t} [p_{t + 1} + d_{t + 1}] = a (p_{t} + d_{t}) + b,$ где $a = φ,$ $b = (1 - φ) ((1 + f) \bar{d} + g),$ а соответствующая условная дисперсия равна $v a r_{t} [p_{t + 1} + d_{t + 1}] = {(1 + f)}^{2} σ_{ε}^{2} .$

Результаты работы агент-ориентированной модели можно непосредственно сопоставить с этим теоретических равновесием. Априори не вполне понятно, покажет ли АОМ результаты, близкие к теоретическим. «Характерной чертой экономической среды является то, что она состоит из агентов, каждый из которых может стараться изучать эту окружающую среду и тем самым то, что делают другие агенты. Это быстро становится очень сложным, и совсем не ясно, будет ли поведение индивидуумов «совместно эволюционировать» к чему-то, соответствующему теоретическому решению для статического равновесия» (Kirman, 2011).

В отличие от (Arthur et al., 1997) мы используем в качестве алгоритма обучения SQ-фильтр. Цена $p_{t}$ играет роль наблюдения $y_{t}$ . Формулу прогноза возьмем линейного вида, но более общую, с разными коэффициентами для цены и дивидендов: $E_{t i} (p_{t}) = a_{t i 1} p_{t} + a_{t i 2} d_{t} + b_{t i} .$ Это дает регрессию с меняющими коэффициентами $β_{t i} = {(a_{t i 1}, a_{t i 2}, b_{t i})}^{T}$ и меняющейся дисперсией $e^{h_{t i}}$ , которую можно использовать в качестве $σ_{t i}^{2} .$ Остальные параметры фильтра были выбраны следующими: $κ = 6$ , $Ω_{β t} = Ω_{β} = d i a g (0,00 3^{2}, 0,01 2^{2}, 0,0 3^{2}),$ ${\tilde{P}}_{β 1} = 100 Ω_{β}$ , $ρ = 0,01$ . Первоначальные значения коэффициентов $β_{1 i}$ выбирались случайно, но достаточно близкими к тем, которые получаются в равновесии с рациональными ожиданиями, если сделать прогнозную функцию линейной не по $p_{t} + d_{t}$ , а по дивидендам $d_{t}$ : $0 \times p_{t} + φ (1 + f) d_{t} + (1 - φ) (1 + f) \bar{d} + g .$

Рис. 1. Динамика коэффициентов $a_{t i 2}$

Рис. 2. Динамика выборочного среднеквадратического отклонения коэффициентов ati2 по агентам

Расчеты по описанной АОМ продемонстрировали следующие основные эффекты.

Параметры $a_{t i 1}, a_{t i 2}, b_{t i}, h_{i t}$ разных агентов сближаются между собой. Это связано с тем, что агенты используют одинаковые алгоритмы обучения и получают одинаковую информацию (рис. 1–2).
Оценка $a_{t i 1}$ колеблется около нулевого уровня, т.е. цена $p_{t}$ не очень информативна для агентов при предсказании $p_{t + 1} + d_{t + 1}$ .
Параметры не сходятся к постоянному уровню, а колеблются в достаточно широких пределах, поскольку агенты постоянно обучаются.
Оценки дисперсии $e^{h_{t i}}$ в среднем выше теоретического аналога ${(1 + f)}^{2} σ_{ε}^{2}$ . Это связано с эффектом из п. 3.
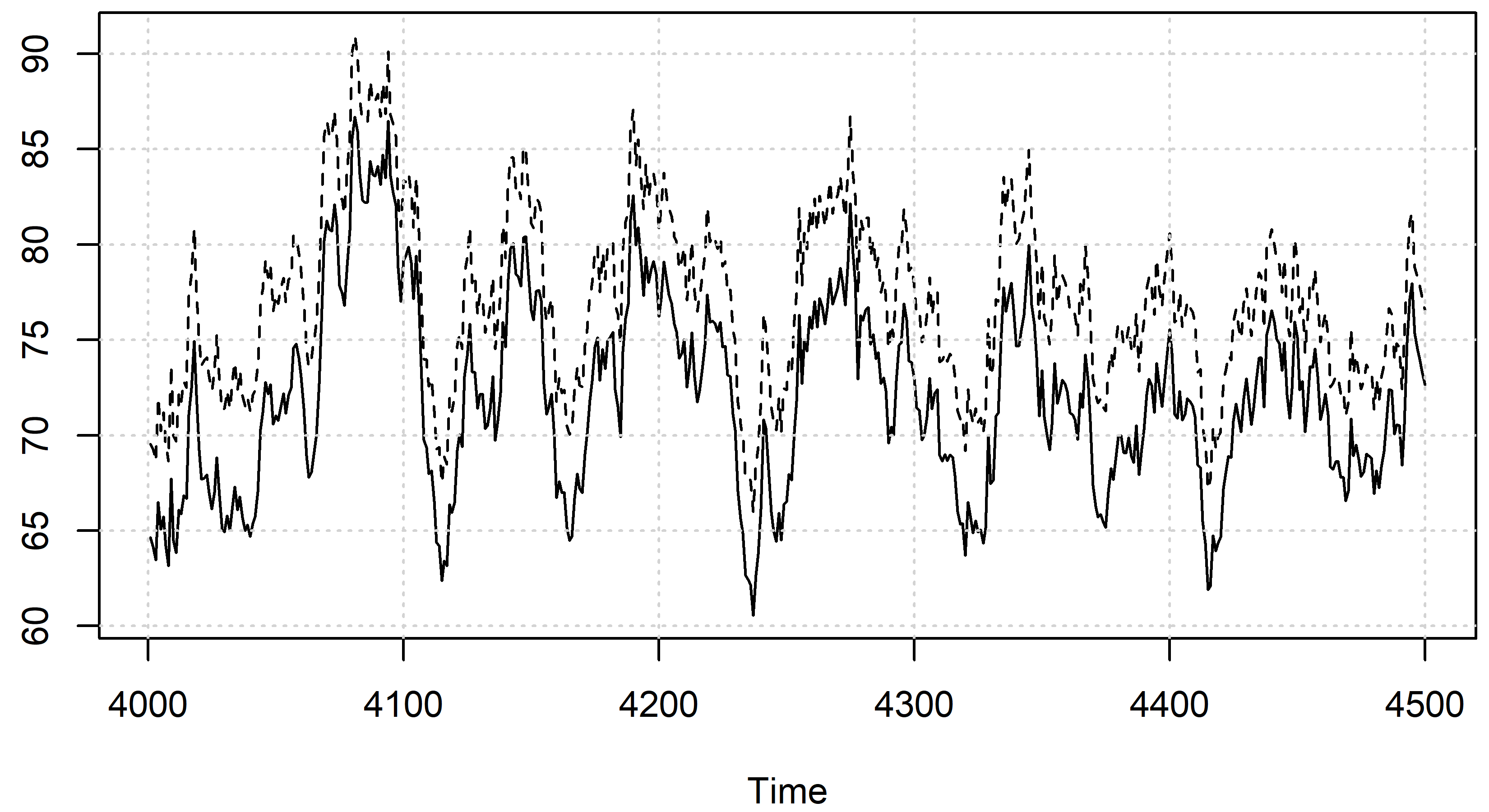
Цена $p_{t}$ в среднем несколько ниже теоретической цены $p_{t}^{R E E}$ (рис. 3). Более того, разница $p_{t}^{R E E} - p_{t}$ положительно коррелирует с оценками дисперсии $e^{h_{t i}}$ у агентов (коэффициент корреляции примерно 0,45). Это объясняется указанным различием дисперсий.

Рис. 3. Типичное поведение двух рядов цен: модельной цены $p_{t}$ (сплошная линия) и «теоретической» $p_{t}^{R E E}$ (пунктир)

Результаты экспериментов демонстрируют, что предложенный алгоритм обучения неплохо работает и обладает правдоподобными свойствами. Однако в рассмотренной постановке модели слабо проявляется тот факт, что каждый агент автономен по поведению и обучению.

Более интересные результаты получаются, если наделить каждого агента в период $t$ некоторой частичной информацией о будущем значении дивиденда $d_{t + 1}$ , причем так, чтобы информация была разная у разных агентов. Не вдаваясь в детали такой модификации модели фондового рынка, отметим, что предложенный алгоритм достаточно правдоподобно работает и в этом случае. А именно оценки параметров у разных агентов уже не сближаются. Оценка параметра $a_{t i 1}$ колеблется около достаточно высокого положительного уровня, что говорит о том, что цена $p_{t}$ в данной модификации становится информативной при предсказании $p_{t + 1} + d_{t + 1}$ .

6. Прогнозы спроса в агент-ориентированной модели российской экономики

Рассматриваемый в статье алгоритм был использован в агент-ориентированной многорегиональной межотраслевой модели (АОМММ), описывающей российскую экономику (см., например, (Цыплаков, 2022) и ссылки там же). В этой модели действует, в частности, механизм торговли, в рамках которого продавцы назначают цены, а покупатели в соответствии с некоторым алгоритмом, включающим элемент случайности, выбирают количества товаров, приобретаемых у тех или иных продавцов. Таким образом, фирмам-продавцам требуется выбрать, какую цену установить.

Спрос на продукцию фирмы зависит от цен, установленных ею и ее конкурентами. Алгоритм покупательского выбора устроен так, что у продавца с более низкой ценой спрос при прочих равных условиях в среднем выше. Кроме того, на общий спрос покупателя-домохозяйства цена также оказывает отрицательное влияние. В целом средний спрос на продукцию фирмы можно представить как воображаемую убывающую функцию ее цены $p_{t}$ .

В каждом периоде фирма имеет некоторые производственные мощности ${\dot{y}}_{t}$ , ограничивающие сверху ее объем производства $y_{t}$ . Также фирма обладает некоторым запасом готовой продукции $S_{t}$ , который она стремится поддерживать на достаточно высоком уровне. Если $D_{t}$ — спрос на продукцию, то за период $t$ запасы готовой продукции изменятся на величину $y_{t} - D_{t}$ . Выбирая цену продукции $p_{t}$ и объем производства $y_{t} \in (0, {\dot{y}}_{t})$ , фирма может влиять на спрос, запасы $S_{t}$ и свою прибыль. В модели фирмы используют оценки функции спроса на свою продукцию $D_{t}^{e} (p_{t})$ для планирования цены и объема производства. По какому именно принципу они это делают, мы здесь не будем обсуждать подробно. Важно, чтобы оценка спроса была достаточно точной и чтобы она адаптировалась к текущей ситуации на рынке. Для решения этой задачи применен алгоритм адаптивной регрессии.

Модель регрессии для отдельной фирмы имеет вид $l n (D_{t} + δ) = - β_{1 t} l n (p_{t}) + β_{2 t} l n ({\bar{p}}_{t}^{o}) + β_{3 t} + ε_{t},$ где $δ > 0$ — небольшая добавка, позволяющая работать с нулевым спросом, ${\bar{p}}_{t}^{o}$ — ожидаемая средняя цена фирм-конкурентов. Для прогнозирования цен конкурентов $p_{t}^{o}$ применяется авторегрессия первого порядка (с тем же адаптивным алгоритмом): $l n (p_{t}^{o}) = γ_{1 t} l n (p_{t - 1}^{o}) + γ_{2 t} + u_{t} .$ В качестве ${\bar{p}}_{t}^{o}$ в модели спроса используется прогноз из этой последней модели.

Были проведены эксперименты по тестированию адаптивных свойств предлагаемого алгоритма. Был взят сценарий сдвига в потребительских предпочтениях, приводящий к изменению потребительского спроса в затронутых отраслях. В АОМММ по умолчанию используются функции полезности Кобба–Дугласа, для которых, как известно, коэффициенты определяют доли отдельных товаров в расходах домохозяйства. За счет увеличения коэффициента для товара 2 (отрасль «Обработка) и уменьшение коэффициента для товара 5 («Услуги») на 5 процентных пунктов в период $t = 100$ были изменены доли соответствующих товаров в расходах. Это повлияло на спрос в этих двух отраслях. Для стабилизации рынков после сдвига требовались изменения в функциях спроса отдельных фирм.

На рис. 4 показана динамика объемов продаж и производства нескольких фирм в отрасли 2 для одного прогона модели. Размеры фирм существенно различаются. Это требует соответствующего установления цен на продукцию — при прочих равных условиях цена на более крупной фирме должна быть более низкой. На этапе инициализации модели этот эффект был учтен, но фирмам все равно потребовался некоторый период обучения, поскольку кроме цены спрос также зависит от местоположения фирмы, ее рынка сбыта и других факторов.

Наблюдается повышательный тренд в объемах производства, связанный с ростом относительной цены продукции в этой отрасли и ростом рентабельности. Объемы продаж следуют этому же тренду. Сразу после периодов $t = 1$ и $t = 100$ продажи для некоторых фирм опережали производство, но адаптация функций спроса привела к постепенному выравниванию этого перекоса.

Рис. 4. Продажи и производство нескольких фирм в отрасли 2

Такую же картину можно наблюдать в агрегированной динамике объемов продаж, производства отрасли 2 (рис. 5). Запасы готовой продукции в два указанных периода адаптации снижались, но затем возвращались к требуемому уровню.

Рис. 5. Продажи, производство и запасы готовой продукции в отрасли 2 в целом

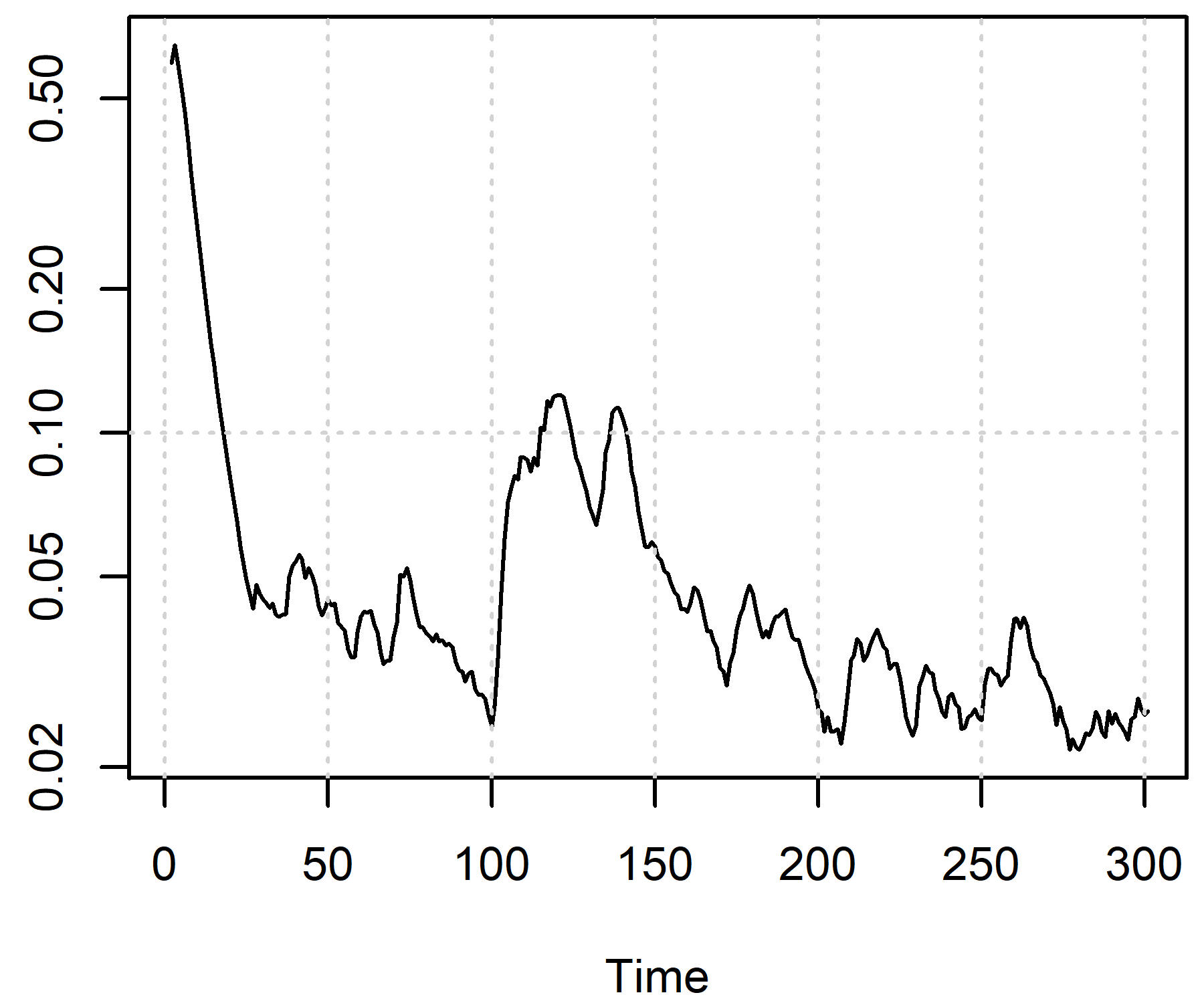
Рис. 6. Средняя неопределенность спроса в отрасли 2

Среднеквадратическое отклонение ошибки $ε_{t}$ в регрессии для спроса равно $e^{h_{t} / 2} .$ Этот ряд можно рассматривать как показатель неопределенности, связанный с предсказанием спроса. В модели АОМММ для мониторинга рассчитывается среднее геометрическое этого показателя, взвешенное по объемам продаж фирм. Динамика средней неопределенности спроса в отрасли 2 показана на рис. 6. После начала работы модели неопределенность спроса находилась на высоком уровне, что связано с тем, что фирмы еще недостаточно изучили свой спрос. Затем неопределенность падает, а после периода $t = 100$ повышается, но до более низкого уровня, чем вначале. Постепенно неопределенность опять падает, так как происходит обучение и фирмы более точно предсказывают спрос на свою продукцию.

7. Заключение

В статье предложен универсальный алгоритм обучения для агент-ориентированных моделей. Основные требования к применимости этого алгоритма — SQ-фильтра — состоят в том, чтобы внутренняя модель мира агента порождала функцию правдоподобия наблюдаемой переменной, которая гладко зависит от параметров, и чтобы можно было в явном виде вычислить соответствующую информационную матрицу. Это позволяет говорить о применимости SQ-фильтра в самых разных видах АОМ (хотя и требуется работа по подбору подходящей удобной для расчетов спецификации зависимости). В частности, хотя здесь это и не обсуждалось, наблюдаемая агентом переменная может быть дискретной, качественной и т.п.

В статье показаны возможности SQ-фильтра на примере моделей окружающего мира, приводящих к линейным регрессиям с t-распределением ошибки. Предложенная адаптивная регрессия хорошо зарекомендовала себя в АОМ при предсказании рыночной цены и при предсказании спроса на продукцию фирмы. В модели искусственного фондового рынка, где агенты-трейдеры обучаются по предложенному алгоритму, обучение происходит вполне качественно и порождает правдоподобные эффекты. В АОМ российской экономики агенты хорошо адаптируются к меняющемуся спросу. В целом приведенные примеры продемонстрировали, что, используя подобный алгоритм, можно наделять агентов правдоподобным поведением, не перегружая модель чрезмерно сложными вычислениями.

Заметим, что в статье за кадром остался вопрос о том, какими выбирать параметры используемых алгоритмов обучения. В (Arthur, 1991) предлагается подход, при котором решения агентов определяются параметризованными алгоритмами принятия решений, и эти алгоритмы подбираются и калибруются таким образом, чтобы поведение агентов достаточно близко соответствовало тому, что наблюдается в реальности. Можно ожидать, что прикладные модели, использующие таких «откалиброванных агентов», будут давать более реалистичные предсказания.

Приложение

Использование QR-разложения для реализации регрессионного SQ-фильтра

Сложности с реализацией описанного регрессионного SQ-фильтра могут возникнуть из-за вычислительной нестабильности при расчетах по рекуррентной формуле для ковариационной матрицы оценок коэффициентов $P_{β, t + 1} = P_{β t} - P_{β t} X_{t}^{T} c_{t}^{- 2} X_{t} P_{β t} + Ω_{β, t + 1} .$ Данная матрица при вычислении непосредственно по указанной формуле может оказаться неположительно определенной. Опишем здесь вычислительный прием, который хорошо зарекомендовал себя на практике — использование QR-разложения.

Пусть $S_{P t}$ — квадратный корень из $P_{β t}$ ; $S_{Ω t}$ — квадратный корень из $Ω_{β, t + 1}$ : $P_{β t} = S_{P t}^{T} S_{P t}, Ω_{β, t + 1} = S_{Ω t}^{T} S_{Ω t} .$ Обозначим

${\hat{c}}_{t} = \sqrt{(κ - 2) (κ + 3) / [κ (κ + 1)] e^{h_{t}}},$ $S_{t} = [\begin{array}{l} {\hat{c}}_{t} & 0 \\ S_{P t} X_{t}^{T} & S_{P t} \\ 0 & S_{Ω t} \end{array}] .$

Тогда

$S_{t}^{T} S_{t} = [\begin{array}{l} {\hat{c}}_{t}^{2} + X_{t} S_{P t}^{T} S_{P t} X_{t}^{T} & X_{t} S_{P t}^{T} S_{P t} \\ S_{P t}^{T} S_{P t} X_{t}^{T} & S_{P t}^{T} S_{P t} + S_{Ω t}^{T} S_{Ω t} \end{array}] = [\begin{array}{l} c_{t}^{2} & X_{t} P_{β t} \\ P_{β t} X_{t}^{T} & P_{β t} + Ω_{β, t + 1} \end{array}] .$

Применим к матрице $S_{t}$ QR-разложение, т.е. представим ее в виде $S_{t} = Q_{t} U_{t},$ где матрица является ортогональной ( ${Q_{t}^{}}^{'} Q_{t} = I$ , $Q_{t} {Q_{t}^{}}^{'} = I$ ), а $U_{t}$ — верхней треугольной. При этом $S_{t}^{T} S_{t} = U_{t}^{T} U_{t} .$ Представим $U_{t}$ в блочном виде, соответствующем структуре $S_{t}$ :

$U_{t} = [\begin{array}{l} U_{t 11} & U_{t 12} \\ 0 & U_{t 13} \\ 0 & 0 \end{array}] .$

Приравнивая $U_{t}^{T} U_{t}$ и $S_{t}^{T} S_{t}$ , получим: $U_{t 11}^{T} U_{t 11} = U_{t 11}^{2} = c_{t}^{2},$ $U_{t 11}^{T} U_{t 12} = U_{t 11} U_{t 12} = X_{t} P_{β t},$ $U_{t 12}^{T} U_{t 12} + U_{t 13}^{T} U_{t 13} = P_{β t} + Ω_{β, t + 1},$ откуда $U_{t 11} = c_{t}$ (берем положительный корень), $U_{t 12} = X_{t} P_{β t} / c_{t}$ и $U_{t 13}^{T} U_{t 13} = P_{β t} - P_{β t} X_{t}^{T} c_{t}^{- 2} X_{t} P_{β t} + Ω_{β, t + 1} = P_{β, t + 1} .$ Таким образом, верхняя треугольная матрица $U_{t}$ имеет вид

$U_{t} = [\begin{array}{l} c_{t} & X_{t} P_{β t} / c_{t} \\ 0 & S_{P, t + 1} \\ 0 & 0 \end{array}] .$

Описанный прием позволяет с помощью стандартного для матричных вычислений QR-разложения получить необходимые для регрессионного SQ-фильтра величины $c_{t}^{2}$ , $X_{t} P_{β t}$ и не теряет положительной полуопределенности.

ГОСТ	Цыплаков А. А. Адаптивная регрессия для агент-ориентированного моделирования // Экономика и математические методы. – 2023. – T. 59. – №4 C. 111-125 . URL: https://emmras.ru/s042473880028256-0-1/?version_id=104400. DOI: 10.31857/S042473880028256-0
MLA	Tsyplakov, Alexander "An adaptive regression for agent-based modeling." Economics and the Mathematical Methods. 59.4 (2023).:111-125. DOI: 10.31857/S042473880028256-0
APA	Tsyplakov A. (2023). An adaptive regression for agent-based modeling. Economics and the Mathematical Methods. vol. 59, no. 4, pp.111-125 DOI: 10.31857/S042473880028256-0

Адаптивная регрессия для агент-ориентированного моделирования

Вы можете

Приложение

Библиография

Адаптивная регрессия для агент-ориентированного моделирования

Вы можете

Приложение

Библиография

Войти через