- PII
- S042473880003315-5-1
- DOI
- 10.31857/S042473880003315-5
- Publication type
- Article
- Status
- Published
- Authors
- Volume/ Edition
- Volume 55 / issue 2
- Pages
- 5-23
- Abstract
to calculate the optimization problem for any number of periods. An optimization method for public investments into projects proposed; it is based on the automatic analysis of “shadow prices” of the linear programming dual problem. A range of experiments are carried, which by means of the graphics illustrate, how various optimization criteria may influence the solution and what consequences they may have in various aspects of the concerned economic environment. For example, if the goal of the regional administration is to increase the financial well-being of the population, then the wage vector is maximized. If the goal of the regional authorities is to increase the profit of any industry or enterprise, then the corresponding vector is maximized. There are many purposes, so the optimization criterion can be combined with different weights corresponding to the tasks facing management. The developed system may be included in the network of situation centers to optimize management solutions at the level of major industrial enterprises, regions or the whole of the country.
- Keywords
- project optimization, project evaluation, linear programming, project economy, long-term planning, Wolfram Mathematica
- Date of publication
- 05.06.2019
- Year of publication
- 2019
- Number of purchasers
- 93
- Views
- 2052
1. Введение
Наступает время проектной экономики, поэтому проекты надо правильно оценивать, расставлять правильные приоритеты для успешного экономического планирования. Планирование нецелесообразно сверхдетально (например, планировать, сколько произвести единиц мороженого), поскольку экономика обладает свойством саморегулирования. Однако планирование является порой необходимой регуляцией со стороны государства на уровне крупных экономических проектов. Управление и оптимизация проектной деятельности государством может обеспечить здоровое функционирование и других отраслей экономики, связанных с конкретным проектом различными финансовыми и товарными отношениями.
В первую очередь оптимальное планирование касается денежных инвестиций в наиболее критические узлы системы (или отрасли), так как финансы являются кровеносной системой любой экономики. Проактивное регулирование экономики со стороны государства актуально, особенно в ситуации геополитической нестабильности, связанной с повышенными импортно-экспортными рисками, оно также необходимо для выявления критических дефицитов любых ресурсов (товарных, человеческих или финансовых) в экономике. Для достижения этих целей нужна адекватная система диагностики экономической ситуации и своевременное грамотное регулирование и планирование. Здесь же встает вопрос о выборе механизма диагностики, т.е. экономических моделей и инструментария.
Известно, что существующие макроэкономические модели общего динамического стохастического равновесия фрагментарны и во многом противоречивы, а также перегружены значительным числом теоретических допущений, параметров и условностей, которые невозможно или очень трудно оценить в реальной экономике (см., например, модели (Ramsey, 1929; Arrow, Debreu, 1954; Samuelson, 1958; Tobin, 1969; Shapiro, Stiglitz, 1984; Blanchard, Fischer, 1989; Bernanke, Gertler, 1995 и др.)), что не позволяет использовать их непосредственно в целях прикладного анализа и планирования.
В свою очередь, эконометрические модели, основанные на анализе статистических данных и выявлении взаимосвязей между экономическими процессами, не требуют выдвижения большого числа априорных предположений об исследуемой системе и практически целиком опираются на эмпирические данные. Однако существенным недостатком моделей данного типа является отсутствие объяснения причин выявленных взаимосвязей.
Возможности и практическое применение упомянутых выше моделей во многом превосходят более поздние агент-ориентированные модели (АОМ) экономики. Отличительной особенностью данных моделей является так называемое моделирование снизу вверх или децентрализованное моделирование, когда изначально неизвестно общее поведение системы, а известны лишь индивидуальные характеристики и алгоритмы поведения агентов (Макаров, Бахтизин, 2013). Области применения АОМ в экономике достаточно широки: финансовая сфера (см. например, работы, (Raberto et al., 2001; LeBaron, 2006; Moiseev, Akhmadeev, 2017), производство (Kutschinski et al., 2003), рынок труда (Tassier, Menczer, 2001), инноватика (Dawid, 2006; Akhmadeev, Manakhov, 2015), бизнес-циклы (Delli Gatti et al., 2008) и многие другие. Преимущество АОМ по сравнению с классическими экономическими моделями общего равновесия заключается в максимальном приближении структуры моделей к реальным социально-экономическими процессам и явлениям. Однако успех применения данных моделей зависит во многом от искусности разработки и адаптации. Преимущества могут превратиться в недостатки при непрофессиональном построении чрезмерно детализированных и нагруженных большим числом параметров моделей, не применимых на практике.
Еще один класс — модели оптимального планирования (ОП), основанные на инструментарии математического программирования. Данный вид моделей широко применялся в середине прошлого века не только в плановой экономике СССР, но и в капиталистических странах, например в США (см. известную модель межотраслевого баланса Леонтьева (Леонтьев, 1951)). В нашей стране основоположником идеи оптимального планирования был академик Л.В. Канторович (Канторович, 1959). В СССР данный вид моделей предназначался для плановой экономики. Однако в условиях перехода к рыночной экономике существенно изменяются сами задачи ОП. Такие модели должны широко применяться в рамках отдельных компаний (предприятий), а в общегосударственных масштабах могут приобретать не директивно-детализированный, а более укрупненный и индикативный характер. Принцип оптимального планирования в комбинации с экономическим анализом, основанным на межотраслевых таблицах типа «затраты–выпуск», являются наглядными инструментами для анализа состояния экономики.
В настоящее время в нашей стране активными темпами идет создание сети ситуационных центров в различных органах федеральной и региональной власти, образовательных учреждениях и крупных промышленных организациях, на что выделяются немалые бюджетные деньги. Целью этих проектов является оперативный мониторинг социально-экономических, природных и других явлений для оптимизации управленческих решений и эффективного планирования. В данном исследовании авторы предпринимают попытку, объединив методы АОМ, линейного программирования и компьютерной оптимизации, построить наиболее адекватную систему планирования и оценки проектов для экономики нашей страны, которую можно будет использовать в таких ситуационных центрах.
Целью работы является разработка инструмента оптимизация экономических проектов, включающая исследование влияния ставок по кредитам, налоговых ставок, уровня накопления в основные фонды, а также других параметров управляющего воздействия на основе комбинированного метода математического и компьютерного программирования.
На упрощенном числовом примере мы показываем, что эффективность проекта существенно зависит от разнородных факторов. Наиболее существенный фактор — критерии оценки проекта. Критериев много, мы перечислим здесь лишь некоторые. Наиболее популярный среди экономистов старой школы критериев — расчетный срок окупаемости вложенных в проект денежных затрат. Но в использовании даже этого критерия могут быть нюансы. Получаемая прибыль может возвращаться инвестору — государственному или частному — она же может направляться разным исполнителям проекта, менять распределение собственности и т.д. Принципиально другой критерий — выполнение проекта в максимально короткий срок. Еще один критерий — наилучшее удовлетворение выполняющих проект работников. Фактор времени в оценке проектов играет критическую роль. В нашем условном примере мы показываем, как меняется оценка эффективности, если в один интервал времени цель проекта — одна, а следовательно, и критерий — один, а в другой интервал цель иная, и, соответственно, существенно корректируется и критерий.
Далее мы специально обращаем внимание на разницу в природе продуктов, фигурирующих в оптимизационной модели. Продуктом могут быть деньги, изобретения, нематериальные шедевры искусства и т.д.
На простом числовом примере мы специально обращаемся к такому продукту, как деньги. Деньги как вид затрат фигурируют во всех способах производства. Поэтому возникает задача создания оптимального количества денег, и задача эта — комплексная, затрагивающая все стороны экономики, она намного сложнее известных из учебников формул связи между количеством денег, ВВП и инфляцией.
Главная же задача нашего исследования, иллюстрируемая расчетами на приводимом здесь примере, состоит в том, как оценивать эффективность нового проекта в зависимости от ряда факторов, в том числе критериев оптимальности, кредитных ставок и пр.
2. Числовая модель для оптимизационных расчетов
Далее в работе приводим упрощенное и формальное представление проектов как векторов, компоненты которых отражают получение благ (продуктов, денег), если число положительное, и затрат, если число отрицательное. Возможности экономики в целом также представлены набором векторов, показывающих возможности производства, финансирования, поведения работников, инвестиций в основные фонды и т.д.
Исходное описание экономики следует классической работе Л.В. Канторовича (Канторович, 1959). Существенное различие состоит лишь в том, что в качестве продукта выступают в том числе деньги.
Алгоритм расчетов, с помощью которого находится оптимальное решение по заданному критерию, представляет собой последовательность действий, среди которых главным является решение оптимизационной задачи, названной далее опорной.
Приводимые ниже численные расчеты можно сгруппировать по двум направлениям. Первое позволяет находить оптимальные траектории развития экономики в зависимости от нескольких принятых в практике критериев. Второе направление позволяет оценивать эффективность новых проектов также в зависимости от исходных данных и критериев оптимальности.
Модель представляет собой финансовую систему закрытого типа, где присутствуют различные типы экономических агентов: банки, кредитующие производителей товаров, а также население, осуществляющее конечное потребление, сами производители различных видов продуктов, которые получают прибыль. Население тратит заработную плату на «конечное потребление», а в случае ее нехватки берет кредит у Центрального банка. Агентами могут являться различные инвестиционные и государственные экономические проекты. Государственный регулятор осуществляет финансирование перспективных проектов через выставление нужного критерия оптимальности для решения актуальных государственных задач.
Опишем модель, о которой говорится выше, более детально, а для этого сформулируем оптимизационную задачу (локальную — для первого года).
Имеется множество N способов производства, или агентов, где интенсивность способа j выражается через число xj и определяет уровень производства конкретного товара. Ниже приводим упрощенный числовой пример задачи оптимального планирования:
1) три агента, каждый из которых производит свой вид товара, они могут представлять три самостоятельных предприятия; 2) три агента, осуществляющих кредитование каждого из вышеперечисленных способов производства; 3) один агент, осуществляющий реализацию конечного потребления (население); 4) один агент, осуществляющий кредитование населения; 5) три агента, выражающих движение рабочей силы от одного производителя к другому.
У каждого агента (отображенного в форме вектора) имеются свои параметры производства (или ресурсы), где знак перед значениями параметров определяет, является ли это затратами или выпуском. В данной задаче 15 различных продуктов: 1) центральный бюджет, выполняющий одновременно функцию центрального банка, 2) финансовые затраты (для каждого из трех производственных предприятий), 3) использование основных средств (для каждого из трех производственных предприятий), 4) производственная матрица, или затраты и выпуск продукции (для каждого из трех производственных предприятий), 5) имеющийся фонд рабочей силы, 6) потребности в рабочей силе трех производственных предприятий, 7) затраты населения на конечное потребление (собственные финансовые ресурсы или кредитные). Конкретные числа приведены в табл. 1.
Таблица 1. Оптимизационная задача для первого года
| НДФЛ, % | 13 | Налог на при-быль, % | 25 | Амортизация, % | 10 | Доля инвестиций в ОС, % | 10 | ||||||||||
| Ставка кредита | Центральный банк | Финансы 1 | Финансы 2 | Финансы 3 | Основные средства 1 | Основные средства 2 | Основные средства 3 | Продукт 1 | Продукт 2 | Продукт 3 | Фонд рабочей силы | Зарплата 1 | Зарплата 2 | Зарплата 3 | Траты населения | Критерий оптимальности | |
| Способ 1 | –1 | –1,1 | 6 | –1,1 | –1 | –1 | 0 | ||||||||||
| Способ 2 | –1 | –1,2 | –1 | 6 | –1 | –1,2 | 0 | ||||||||||
| Способ 3 | –1 | –0,98 | –1 | –0,9 | 5 | –0,9 | 0 | ||||||||||
| Банк1 | 0,1 | –1 | 1 | 0 | |||||||||||||
| Банк 2 | 0,1 | –1 | 1 | 0 | |||||||||||||
| Банк 3 | 0,1 | –1 | 1 | 0 | |||||||||||||
| Конечное потребление | 0 | –0,9 | –1,1 | –2 | 1 | ||||||||||||
| Заработная плата 1 | –1 | 1 | 1 | 0 | |||||||||||||
| Заработная плата 2 | –1 | 1 | 1 | 0 | |||||||||||||
| Заработная плата 3 | –1 | 1 | 1 | 0 | |||||||||||||
| Потребительский банк | –1 | 1 | 0 | ||||||||||||||
| Вектор ограничений ресурсов | –10 | –0,5 | –0,5 | –0,5 | –1 | –1 | –1 | 0 | 0 | 0 | –15 | 0 | 0 | 0 | 0 | ||
| Знак ограничения | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Примечание. Последний столбец в табл. 1 — вектор критерия оптимальности C, не входящий в матрицу А. Вторая строка снизу — вектор B — ограничения на ресурсы: финансовые затраты, производственные фонды, рабочая сила и т.д. В последней строке — знак ограничения на ресурс bj в векторе B: 1 означает «>», 0 — «=» и –1 — «
3. Решение опорной задачи на максимум
В общем виде опорная задача представляет собой стандартную оптимизационную задачу (1):


 (1)
(1)
Распишем эту задачу более подробно, исходя из данных, приведенных в табл. 1:
 (2)
(2)
Задача оптимизации заключается в максимизации конечного потребления продукции с коэффициентом 1. Среда программирования Wolfram Mathematica автоматически приводит систему ограничений к каноническому виду. После решения данной задачи программа находит значения вектора X, т.е. интенсивности выполнения каждого из производственных способов. В табл. 2 приведены результаты решения прямой задачи для периода 1.
Таблица 2. Результат решения задачи на период 1
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 |
| 0,30 | 0,76 | 1,02 | 0,00 | 0,26 | 0,52 | 3,68 | 0,30 | 0,91 | 0,92 | 5,23 |
Проведем краткий анализ: как видно из решения данной задачи, производственное предприятие 1 не воспользовалось кредитом (x4 = 0), выдаваемым центральным банком, а интенсивность самого способа производства предприятия 1 (x1) равна 0,30, что могло произойти из-за дефицита (недостатка) одного из ресурсов, о чем будет сказано ниже при решении двойственной задачи. А предприятие 3 сработало сверх нормы (норма интенсивности равна единице), интенсивность производственного способа (x3) равна 1,02. Как отмечалось выше, в данной задаче единственным критерием оптимальности является максимизация конечного потребления. Интенсивности производственных способов задаются решением оптимизационной задачи таким образом, чтобы задать максимальное конечное потребление в рамках имеющихся ограничений ресурсов.
Данная задача линейного программирования описана Л.В. Канторовичем в его знаменитой книге (Канторович, 1959), за которую он получил Нобелевскую премию. Отличие настоящей модели состоит в том, что в качестве продуктов (параметров) фигурируют не только обычные продукты, фонды и услуги, но и сами деньги (кредитные). Об этом говорится подробнее ниже.
Для того чтобы проанализировать результаты решения данной оптимизационной задачи, необходимо решить двойственную задачу, а также произвести необходимые вычисления для построения задачи на следующий период.
4. Решение двойственной задачи
Решение двойственной задачи предполагает нахождение называемых Л.В. Канторовичем объективно-обусловленных оценок (о.о. оценки) на каждый из ресурсов. В классической оптимизационной проблеме решение двойственной задачи означает нахождение оценок на ресурсы, указанные в ограничениях (вектор B), при продаже которых мы бы получили доход не меньше того, который образуется в случае использовании ресурсов для производства нашими способами, при этом доход или цена при продаже произведенной продукции указывается в векторе C. В классическом виде она формулируется следующим образом:
 (3)
(3)
где B — вектор ресурсов, A — производственная матрица, Y — оценки ресурсов.
Система Wolfram Mathematica решает эту задачу автоматически на основании исходных данных, поэтому не нужно транспонировать матрицы ограничений и подготавливать данные для ее решения. В табл. 3 отображены объективно-обусловленные оценки ресурсов при решении двойственной задачи для периода 1.
Таблица 3. Результат решения двойственной задачи для периода 1
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 | y11 | y12 | y13 | y14 | y15 |
| 0,00 | 0,00 | 0,01 | 0,01 | 0,00 | 0,00 | 3,68 | 0,16 | 0,16 | 0,78 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
Далее, зная о.о. оценки ресурсов, а в данном случае это — продукт 1 (y8 = 0,16), продукт 2 (y9 = 0,16) и продукт 3 (y10 = 0,78), можем определить дефицитность каждого ресурса. Математический смысл данных оценок заключается в определении того, на сколько увеличится (уменьшится) значение целевой функции при увеличении (уменьшении) запаса данного ресурса на одну единицу. В нашем случае самым дефицитным является продукт 3 с о.о. оценкой, равной 0,78, а также наблюдается острая нехватка ОС для того же предприятия 3 (y7) с оценкой, равной 3,68. На этом основании мы делаем вывод о том, что, повысив объемы ОС для предприятия 3 и, соответственно, произведя больше продукта 3, мы добьемся большего прироста целевой функции. Выше было доказано, что при решении основной задачи увеличение интенсивности 3 производственного способа (производства продукта 3) дает больший прирост конечного потребления (целевой функции).
5. Обновление ограничений для решения задачи на следующий период
Распишем пошаговый алгоритм пересчета данных для решения прогностической задачи на несколько периодов.
1. Покажем, как считается прибыль для предприятия 1: интенсивность способа производства определяется через x1. На это значение умножается сумма: операционных затрат, разницы между прямыми затратами и доходом от реализации произведенной продукции, затрат на заработную плату и отчислений на амортизацию ОС; затем также вычитается налог на прибыль:
 ,(4)
,(4)
где  — операционная прибыль предприятия 1 на период
— операционная прибыль предприятия 1 на период  ,
,  — сумма операционных затрат,
— сумма операционных затрат,  — разница между суммой прямых затрат и доходом от реализации произведенной продукции,
— разница между суммой прямых затрат и доходом от реализации произведенной продукции,  — сумма затрат на заработную плату,
— сумма затрат на заработную плату,  — стоимость ОС предприятия 1, выраженная как ограничение ресурса 5 в векторе B,
— стоимость ОС предприятия 1, выраженная как ограничение ресурса 5 в векторе B,  — ставка амортизационных отчислений на ОС,
— ставка амортизационных отчислений на ОС,  — ставка налога на прибыль.
— ставка налога на прибыль.
2. Сумма налога на прибыль всех трех предприятий возвращается в центральный бюджет  :
:
 (5)
(5)
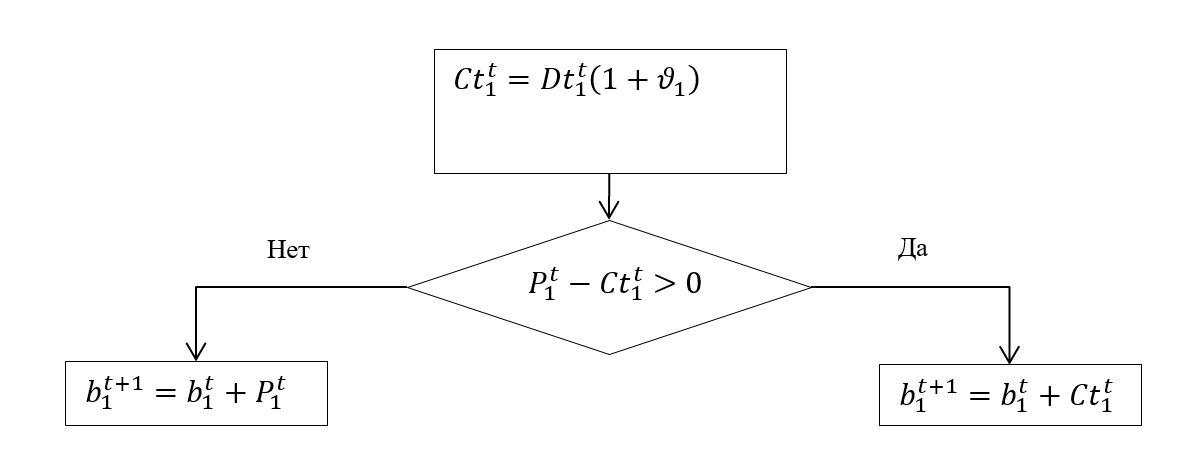
3. Алгоритм возврата сумм кредитных процентов для предприятия 1 представлен на рис. 1. Если прибыль больше полученного кредита, кредит полностью возвращается, а остаток прибыли (чистая прибыль) записывается на баланс предприятия и переносится на следующий период со знаком «+», если меньше, то вся прибыль уходит на погашение кредита, а кредитный долг записывается на баланс предприятия со знаком «—»:
4. Расчет амортизации ОС для периода  , инвестирование государством части бюджета в ОС производственного предприятия 1 (
, инвестирование государством части бюджета в ОС производственного предприятия 1 ( ) и вычет инвестированной суммы из бюджета
) и вычет инвестированной суммы из бюджета  :
:
 , —(6)
, —(6)
и вычет инвестированной суммы из баланса
 (7)
(7)
где  — амортизационная ставка на ОС предприятия 1,
— амортизационная ставка на ОС предприятия 1,  — центральный бюджет в следующий период,
— центральный бюджет в следующий период,  — сумма инвестиций в ОС предприятия 1.
— сумма инвестиций в ОС предприятия 1.
5. Возврат суммы НДФЛ предприятия 1 в ЦБ:
 (8)
(8)
где  — интенсивность использования рабочей силы для предприятия 1,
— интенсивность использования рабочей силы для предприятия 1,  — ставка НДФЛ (в долях).
— ставка НДФЛ (в долях).
6. Естественный прирост населения:
 (9) где
(9) где  — ограничение на человеческие ресурсы,
— ограничение на человеческие ресурсы,  — доля естественного прироста.
— доля естественного прироста.
6. Решение прогностической задачи на несколько периодов
После определения основных параметров задачи и формул их расчета для следующего периода решается задача алгоритмического прогнозирования на несколько периодов. Суть алгоритма заключается в использовании экономического смысла о.о. оценок для корректировки размера инвестиций в ОС с целью увеличения объема конечного потребления в долгосрочной перспективе. То есть инвестировать больше денег в ОС более дефицитных продуктов. Размер инвестиций, согласно формуле (6), определяется фиксированной ставкой  и назначается экзогенно центральным аппаратом (государством).
и назначается экзогенно центральным аппаратом (государством).
Описываемый ниже алгоритм предполагает, что государство, исходя из решения общей оптимизационной задачи, инвестирует в проекты скорректированную сумму. Например, если уровень дефицита продукта 1 в предыдущем периоде был в 0,78, то в ОС предприятия, производящего продукт 1, инвестируется именно эта сумма.
Соответственно, в формуле (6) параметр корректируется следующим образом:
 (10)
(10)
где  — о.о. оценка продукта j.
— о.о. оценка продукта j.
В нашем примере, как видно из табл. 3, дефицит продуктов 1—3 распределен следующим образом: 0,16 — первый ( ); 0,16 — второй (
); 0,16 — второй ( ); 0,78 — третий (
); 0,78 — третий ( ). В табл. 4 представлена таблица с производственной матрицей и пересчетом вектора B для периода 2.
). В табл. 4 представлена таблица с производственной матрицей и пересчетом вектора B для периода 2.
Таблица 4. Ограничения параметров с пересчетом для периода 2
| НДФЛ, % | 13 | Налог на при-быль, % | 25 | Амортизация, % | 10 | Доля инвестиций в ОС, % | 10 | ||||||||||
| Ставка кредита | Центральный банк | Финансы 1 | Финансы 2 | Финансы 3 | Основные средства 1 | Основные средства 2 | Основные средства 3 | Продукт 1 | Продукт 2 | Продукт 3 | Фонд рабочей силы | Зарплата 1 | Зарплата 2 | Зарплата 3 | Траты населения | Критерий оптимальности | |
| Способ 1 | –1 | –1,1 | 6 | –1,1 | –1 | –1 | 0 | ||||||||||
| Способ 2 | –1 | –1,2 | –1 | 6 | –1 | –1,2 | 0 | ||||||||||
| Способ 3 | –1 | –0,98 | –1 | –0,9 | 5 | –0,9 | 0 | ||||||||||
| Банк 1 | 0,1 | –1 | 1 | 0 | |||||||||||||
| Банк 2 | 0,1 | –1 | 1 | 0 | |||||||||||||
| Банк 3 | 0,1 | –1 | 1 | 0 | |||||||||||||
| Конечное потребление | 0 | –0,9 | –1,1 | –2 | 1 | ||||||||||||
| Зарплата 1 | –1 | 1 | 1 | 0 | |||||||||||||
| Зарплата 2 | –1 | 1 | 1 | 0 | |||||||||||||
| Зарплата 3 | –1 | 1 | 1 | 0 | |||||||||||||
| Потребительский банк | –1 | 1 | 0 | ||||||||||||||
| Вектор ограничений ресурсов | –10,49 | –0,39 | –0,67 | –0,27 | –1,05 | –1,05 | –1,68 | 0 | 0 | 0 | –15,15 | 0 | 0 | 0 | 0 | ||
| Знак ограничения | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
При решении прогностической задачи на несколько периодов данный перерасчет ограничений ресурсов производится по окончании каждого периода. Далее мы продемонстрируем ряд наших экспериментов.
6.1. Эксперимент 1. Инвестиции с опорой на объективно-обусловленные оценки. Проведем следующий эксперимент в двух режимах:
1) инвестируем в ОС трех предприятий не фиксированную ставку  , а сумму, выраженную в о.о. оценке данного ресурса
, а сумму, выраженную в о.о. оценке данного ресурса  ; 2) инвестируем фиксированную сумму
; 2) инвестируем фиксированную сумму  , равную средней сумме инвестиций в режиме 1, так чтобы суммарный объем инвестиций был одинаковым.
, равную средней сумме инвестиций в режиме 1, так чтобы суммарный объем инвестиций был одинаковым.
Решим оптимизационную задачу с расчетом на 50 периодов. В качестве показателей эффективности примем: 1) уровень конечного потребления, 2) объем центрального бюджета 3) финансовый баланс трех предприятий (общую сумму) в обоих случаях к периоду 50, 4) показатель ROI (доходность инвестированного капитала) — отношение суммарного дохода на суммарные инвестиции за все периоды моделирования.
Таблица 5. Результаты эксперимента по оценке эффективности инвестиций
| Критерии оценки | Инвестиции с | |
| о.о. оценками | фиксированной суммой | |
| Суммарный объем инвестиций в ОС в денежных единицах | 68,48 | 68,48 |
| Интенсивность конечного потребления в период 50 | 42,26 | 42,26 |
| Объем центрального бюджета к периоду 50 | 71,53 | 69,84 |
| Накопленная интенсивность конечного потребления | 1491,65 | 1468,4 |
| Сумма финансового баланса трех предприятий | 1140,14 | 1122,03 |
| ROI, % | 190 | 187 |
Результаты эксперимента, отраженные в табл. 5, показывают, что по всем показателям (кроме уровня конечного потребления в период 50) режим 1 демонстрирует лучшие результаты и более эффективное распределение инвестиционных средств в экономике.
График на рис. 2 показывает, что эксперимент в режиме 1 дает доходность инвестиций (ROI) в среднем на 20% выше, однако ближе к периоду 50 графики начинают сходиться. Из этого можно сделать следующие выводы: дефицит различных продуктов с течением времени устраняется, а предложенный метод инвестиции наиболее эффективно работает именно в случае с большим разбросом дефицитности различных продуктов.
6.2. Эксперимент 2. Поиск параметров, максимизирующих функцию полезности. Данный эксперимент проводится путем подбора чисел для определения оптимальных параметров управляющего воздействия, в качестве которых была выбрана ставка налога на прибыль и кредитная ставка центрального банка. В качестве целевой функции выбран показатель накоплений центрального бюджета за 50 периодов моделирования (табл. 6).
Таблица 6. Исходные данные и результаты эксперимента
| Данные | Кредитная ставка ЦБ,% | Ставка налога на прибыль,% |
| Границы перебора параметров управляющего воздействия (т.е. численная оптимизация путем подбора параметров в компьютерной программе) | 0, …, 30 | 0, …, 100 |
| Шаг перебора параметров управляющего воздействия | 1 | 5 |
| Управляющие параметры, при которых достигнуто максимальное значение целевой функции (т.е. точка, при которой ЦБ накопил наибольшее количество денег) | 2 | 25 |
На рис. 3 показаны значения управляющих параметров (по осям x и y) и целевой функции (по оси z).
Таким образом, в результате эксперимента 2 были выявлены оптимальные ставки по кредитам и налогу на прибыль. При сравнении с реальными ставками в Российской Федерации налог на прибыль находится почти на таком же уровне (24% — в РФ), а ставка по кредиту (в среднем — 10%) намного выше оптимальной, согласно эксперименту, проведенному выше. Как можно видеть на рис. 4, для налога на прибыль область допустимых значений лежит между 0 и 30%, т.е. при ставке больше 30% бюджет перестает накапливаться. Это связано с тем, что при такой ставке прибыли компаний недостаточно, чтобы платить по счетам, в том числе по кредитным, и компании ликвидируются. По условию алгоритма пересчета прибыли, если кредитный долг какой-либо компании превышает сумму центрального бюджета, она объявляется банкротом и ликвидируется.
На рис. 4 наглядно видно, что уровень конечного потребления не зависит от изменения данных параметров. Однако есть допустимые границы, в рамках которых популяция производственных компаний продолжает существовать и оставаться прибыльными. Например, при ставке налога на прибыль более 35% одна или больше компаний не доживает до периода 50 моделирования. Они становятся убыточными и ликвидируются. Сравнивая эти два критерия оптимальности (рис. 4 и 5), мы видим, что области допустимых значений в обоих случаях примерно совпадают.
6.3. Эксперимент 3. Оценка эффективности ввода в эксплуатацию нового проекта.
Выше мы продемонстрировали возможности системы на простейших числовых примерах с тремя предприятиями, производящими продукты 1—3, причем каждое — со своей эффективностью и объемом привлекаемых ресурсов. Для данного эксперимента был выбран новый пример с четырьмя предприятиями и новыми значениями производственной матрицы A.
Предположим, что в определенном регионе развито машиностроение. Руководство региона решило модернизировать эту отрасль, создав новые способы производства (внедрить инновации), и объявило конкурс проектов производства машин, на который подали свои бизнес-проекты два новых предприятия, которые до этого не работали в регионе. Для удобства анализа модель экономики упрощена до производства трех различных продуктов: машины, металл и пластик. Традиционный способ производства назван «способ 1», а два новых — «способ 2» (табл. 7) и «способ 3» (табл. 8). Теперь продукт (например, «машины») может быть произведен не только основным, но и дополнительными и оригинальными способами, у которых будет другая эффективность производства. Далее мы проведем эксперименты и сравним эффективности этих дополнительных (отличающихся друг от друга) способов производства машин при различных же критериях оптимальности. Таким образом мы покажем, как проекты могут быть оценены не только с точки зрения прибыльности предприятий и принятых классических финансовых показателей оценки проектов (ROI, срок окупаемости инвестиций и др.), но и с позиции эффективности конкретного проекта для всей экономики в зависимости от того, что мы будем считать благом: прирост центрального бюджета, рост конечного потребления, прибыли самих компаний либо рост заработных плат для населения и т.д.
Таблица 7. Ввод в эксплуатацию завода (нового проекта) для производства машин (способ 2)
| НДФЛ, % | 13 | Налог на при-быль, % | 25 | Амортизация, % | 0 | Доля инвестиций в ОС, % | 10 | |||||||||||||
| Ставка кредита | Центральный банк | Финансы 1 | Финансы 2 | Финансы 3 | Финансы 4 | Основные средства 1 | Основные средства 2 | Основные средства 3 | Основные средства 4 | Машины | Пластик | Металл | Фонд рабочей силы | Заработная плата 1 | Заработная плата 2 | Заработная плата 3 | Заработная плата 4 | Траты населения | Критерий оптимальности | |
| 1. Производство машин (способ 1) | –10560 | –11000 | 38000 | –2000 | –5500 | –8000 | 0 | |||||||||||||
| 2. Производство машин (способ 2) | –6500 | –10000 | 29000 | –2000 | –3000 | –6000 | 0 | |||||||||||||
| 3. Производство пластика | –2600 | –12900 | –5000 | 18500 | –2000 | –5000 | 0 | |||||||||||||
| 4. Производство металла | –2300 | –11000 | –7000 | –1300 | 19 000 | –4400 | 0 | |||||||||||||
| Банк 1 | 0,1 | –1 | 1 | 0 | ||||||||||||||||
| Банк 2 | 0,1 | –1 | 1 | 0 | ||||||||||||||||
| Банк 3 | 0,1 | –1 | 1 | 0 | ||||||||||||||||
| Банк 4 | 0,1 | –1 | 1 | 0 | ||||||||||||||||
| Конечное потребление | –5000 | –5000 | 0 | |||||||||||||||||
| Заработная плата 1 | –1 | 1 | 1 | 1 | ||||||||||||||||
| Заработная плата 2 | –1 | 1 | 1 | 1 | ||||||||||||||||
| Заработная плата 3 | –1 | 1 | 1 | 1 | ||||||||||||||||
| Заработная плата 4 | –1 | 1 | 1 | 1 | ||||||||||||||||
| Потребительский банк | –1 | 1 | 0 | |||||||||||||||||
| Вектор ограничений ресурсов | –50000 | –10000 | –6000 | –2900 | –3000 | –15000 | –10000 | –12000 | –10000 | 0 | 0 | 0 | –25000 | 0 | 0 | 0 | 0 | 0 | ||
| Знак ограничения | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
Таблица 8. Ввод в эксплуатацию завода (нового проекта) для производства машин (способ 3)
| НДФЛ, % | 13 | Налог на прибыль, % | 25 | Амортизация, % | 0 | Доля инвестиций в ОС, % | 10 | |||||||||||||
| Ставка кредита | Центральный банк | Финансы 1 | Финансы 2 | Финансы 3 | Финансы 4 | Основные средства 1 | Основные средства 2 | Основные средства 3 | Основные средства 4 | Машины | Пластик | Металл | Фонд рабочей силы | Зарплата 1 | Зарплата 2 | Зарплата 3 | Зарплата 4 | Траты населения | Критерий оптимальности | |
| 1. Производство машин (способ 1) | –10560 | –11000 | 38 000 | –2000 | –5500 | –8000 | 0 | |||||||||||||
| 2. Производство машин (способ 3) | –4500 | –10000 | 29 000 | –1000 | –4000 | –8000 | 0 | |||||||||||||
| 3. Производство пластика | –2600 | –12900 | –5000 | 18500 | –2000 | –5000 | 0 | |||||||||||||
| 4. Производство металла | –2300 | –11 000 | –7000 | –1300 | 19 000 | –4400 | 0 | |||||||||||||
| Банк 1 | 0,1 | –1 | 1 | 0 | ||||||||||||||||
| Банк 2 | 0,1 | –1 | 1 | 0 | ||||||||||||||||
| Банк 3 | 0,1 | –1 | 1 | 0 | ||||||||||||||||
| Банк 4 | 0,1 | –1 | 1 | 0 | ||||||||||||||||
| Конечное потребление | –5000 | –5000 | 0 | |||||||||||||||||
| Заработная плата 1 | –1 | 1 | 1 | 1 | ||||||||||||||||
| Заработная плата 2 | –1 | 1 | 1 | 1 | ||||||||||||||||
| Заработная плата 3 | –1 | 1 | 1 | 1 | ||||||||||||||||
| Заработная плата 4 | –1 | 1 | 1 | 1 | ||||||||||||||||
| Потребительский банк | –1 | 1 | 0 | |||||||||||||||||
| Вектор ограничений ресурсов | –50 000 | –10 000 | –6000 | –2900 | –3000 | –15 000 | –10 000 | –12 000 | –10 000 | 0 | 0 | 0 | –25 000 | 0 | 0 | 0 | 0 | 0 | ||
| Знак ограничения | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
Как видим из данных табл. 7 и 8, способы производства машин 2 и 3 отличаются потреблением количества различных ресурсов, например, способ 3 потребляет больше металла (4000 тыс. руб.), но меньше пластика (1000 тыс. руб.) по сравнению со способом 2 (3000 тыс. и 2000 тыс. руб. соответственно), начальные финансовые инвестиции и ОС выделяются обоим проектам в одинаковом размере. Налог на прибыль (25%), НДФЛ (13%) и ставка амортизации (1%) остаются на прежнем уровне, как и определенный в эксперименте 1 алгоритм инвестирования в ОС.
Определим прибыльность данных проектов. Напомним, что прибыль считается по формуле (4). Как для способа 2, так и для способа 3 производства машин она равна 11 400 тыс. руб. за один период при интенсивности выполнения способа, равной 1, что ставит наши инвестиционные проекты в равные изначальные условия.
Итак, начнем сами эксперименты. Для начала выберем стандартный для рыночной экономики критерий оптимальности (с точки зрения руководства региона) — максимизацию конечного потребления, соответственно, мы видим 1 в векторе C в строке «конечное потребление» (табл. 7, 8). В табл. 9 и 10 приведены решения обозначенных выше оптимизационных задач с интенсивностью применения каждого способа для десяти периодов моделирования.
Таблица 9. Интенсивность способов производства с добавлением способа 2 при максимизации конечного потребления (интенсивность использования способа производства)
| Пери-од | Производство | Банк | Конечное потребление | Заработная плата | |||||||||
| Машины (способ 1) | Машины (способ 2) | Пластик | Металл | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
| 1 | 1,35 | 1,00 | 0,93 | 0,80 | 4298 | 500,00 | 0,00 | 0,00 | 14,04 | 10 831 | 6000 | 4651 | 3517 |
| 2 | 1,39 | 1,04 | 0,34 | 0,60 | 7302 | 0,00 | 0,00 | 0,00 | 15,41 | 11 135 | 6217 | 1687 | 2649 |
| 3 | 1,52 | 1,18 | 0,34 | 0,66 | 4544 | 0,00 | 0,00 | 0,00 | 17,12 | 12 147 | 7081 | 1691 | 2910 |
| 4 | 1,50 | 1,17 | 0,34 | 0,66 | 0,00 | 0,00 | 0,00 | 0,00 | 16,97 | 12 040 | 7022 | 1676 | 2885 |
| 5 | 1,49 | 1,16 | 0,33 | 0,65 | 0,00 | 0,00 | 0,00 | 0,00 | 16,83 | 11 934 | 6964 | 1662 | 2860 |
| 6 | 1,48 | 1,15 | 0,33 | 0,64 | 0,00 | 0,00 | 0,00 | 0,00 | 16,68 | 11 829 | 6906 | 1648 | 2836 |
| 7 | 1,47 | 1,14 | 0,33 | 0,64 | 0,00 | 0,00 | 0,00 | 0,00 | 16,54 | 11 725 | 6849 | 1634 | 2811 |
| 8 | 1,45 | 1,13 | 0,32 | 0,63 | 0,00 | 0,00 | 0,00 | 0,00 | 16,40 | 11 623 | 6792 | 1620 | 2787 |
| 9 | 1,44 | 1,12 | 0,32 | 0,63 | 0,00 | 0,00 | 0,00 | 0,00 | 16,26 | 11 521 | 6736 | 1606 | 2763 |
| 10 | 1,43 | 1,11 | 0,32 | 0,62 | 0,00 | 0,00 | 0,00 | 0,00 | 16,12 | 11 420 | 6681 | 1592 | 2739 |
Таблица 10. Интенсивность способов производства с добавлением способа 3 при максимизации конечного потребления (интенсивность использования способа производства)
| Период | Производство | Банк | Конечное потребление | Заработная плата | |||||||||
| Машины (способ 1) | Машин ы(способ 3) | Пластик | Металл | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
| 1 | 1,32 | 1,00 | 0,70 | 0,67 | 3953 | 0,00 | 0,00 | 0,00 | 14,21 | 10 570 | 8000 | 3496 | 2933 |
| 2 | 1,39 | 1,04 | 0,25 | 0,65 | 7215 | 0,00 | 0,00 | 0,00 | 15,43 | 11 135 | 8289 | 1260 | 2849 |
| 3 | 1,52 | 1,06 | 0,27 | 0,69 | 4653 | 0,00 | 0,00 | 0,00 | 16,44 | 12 147 | 8465 | 1349 | 3039 |
| 4 | 1,50 | 1,07 | 0,27 | 0,69 | 0,00 | 0,00 | 0,00 | 0,00 | 16,42 | 12 040 | 8580 | 1346 | 3035 |
| 5 | 1,49 | 1,09 | 0,27 | 0,69 | 0,00 | 0,00 | 0,00 | 0,00 | 16,41 | 11 934 | 8693 | 1342 | 3031 |
| 6 | 1,48 | 1,10 | 0,27 | 0,69 | 0,00 | 0,00 | 0,00 | 0,00 | 16,39 | 11 829 | 8806 | 1338 | 3027 |
| 7 | 1,47 | 1,11 | 0,27 | 0,69 | 0,00 | 0,00 | 0,00 | 0,00 | 16,37 | 11 725 | 8917 | 1335 | 3023 |
| 8 | 1,45 | 1,13 | 0,27 | 0,69 | 0,00 | 0,00 | 0,00 | 0,00 | 16,36 | 11 623 | 9027 | 1331 | 3019 |
| 9 | 1,44 | 1,12 | 0,26 | 0,68 | 0,00 | 0,00 | 0,00 | 0,00 | 16,24 | 11 521 | 8982 | 1321 | 2997 |
| 10 | 1,43 | 1,11 | 0,26 | 0,68 | 0,00 | 0,00 | 0,00 | 0,00 | 16,10 | 11 420 | 8908 | 1310 | 2971 |
В табл. 11 и 12 приведены изменения значений капитала 4 модельных предприятий в течение десяти периодов моделирования, что потребуется нам для дальнейшей оценки и анализа.
Таблица 11. Изменение капитала четырех предприятий при вводе способа 2 производства машин, тыс. руб.
| Период | Производство машин | Производство пластика | Производство металла | |
| Способ 1 | Способ 2 | |||
| 1 | 7397 | 8075 | 2721 | 2398 |
| 2 | 11 490 | 16 700 | 5442 | 4796 |
| 3 | 18 616 | 25 325 | 8163 | 7195 |
| 4 | 30 741 | 33 950 | 10 884 | 9593 |
| 5 | 42 865 | 42 575 | 13 605 | 11 991 |
| 6 | 54 990 | 51 200 | 16 326 | 14 389 |
| 7 | 67 114 | 59 825 | 19 047 | 16 787 |
| 8 | 79 239 | 68 450 | 21 767 | 19 186 |
| 9 | 91 363 | 77 075 | 24 488 | 21 584 |
| 10 | 103 488 | 85 700 | 27 209 | 23 982 |
Таблица 12. Изменение капитала четырех предприятий при вводе способа 3 производства машин, тыс. руб.
| Период | Производство машин | Производство пластика | Производство металла | |
| Способ 1 | Способ 3 | |||
| 1 | 7484 | 8625 | 2045 | 2000 |
| 2 | 11 380 | 17 250 | 4091 | 4000 |
| 3 | 18 094 | 25 875 | 6136 | 6000 |
| 4 | 29 926 | 34 500 | 8182 | 7999 |
| 5 | 41 758 | 43 125 | 10 227 | 9999 |
| 6 | 53 591 | 51 750 | 12 272 | 11 999 |
| 7 | 65 423 | 60 375 | 14 318 | 13 999 |
| 8 | 77 255 | 69 000 | 16 363 | 15 999 |
| 9 | 89 088 | 77 625 | 18 409 | 17 999 |
| 10 | 100 920 | 86 250 | 20 454 | 19 999 |
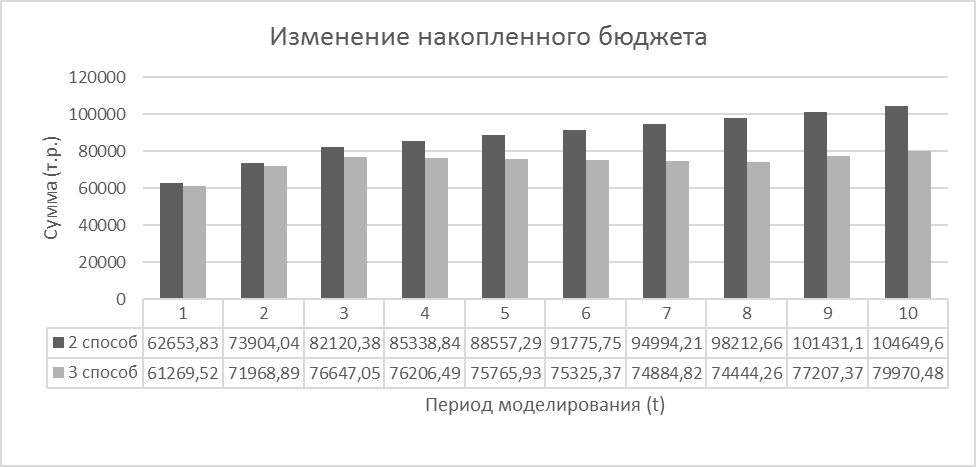
На рис. 5 представлены значения накоплений центрального бюджета за все десять периодов.
Проведем сначала оценку самих способов производства машин и покажем их эффективность по нескольким классическим критериям: доходность инвестированного капитала (ROI) за десять периодов и срок окупаемости инвестиций:
Для первого изначального предприятия этот показатель отличается в эксперименте 1 и 2:
Во-первых, значения способов производства 2 и 3 машин отличаются незначительно, но все же можно уверенно утверждать, что они более привлекательны в качестве инвестиционного объекта по сравнению с традиционным способом 1, одновременно способ 2 ненамного более привлекательный, чем способ 3.
Во-вторых, для расчета срока окупаемости инвестиций, сумма начальных инвестиций проекта 1 равна: 10 000 тыс. руб. (финансовые инвестиции) + 15 000 тыс. руб. (инвестиции в ОС) = 25 000 тыс. руб.
К периоду 3 капитализация проекта 1 равна 18 616 и 18 094 тыс. руб. (при использовании добавочного способа 2 и 3 соответственно), к периоду 4 равна 30 741 и 29 926 тыс. руб., соответственно, срок окупаемости — четыре периода в обоих случаях. Для способов 2 и 3 аналогичным приемом подсчета получаем: срок окупаемости проекта — два периода для обоих способов.
По данным показателям новые проекты выглядят более привлекательными, причем способ 2 ( обеспечивает немного больший возврат инвестиций, чем способ 3 (
обеспечивает немного больший возврат инвестиций, чем способ 3 ( . Остается выяснить, внедрение которого из них будет более полезным с точки зрения всей экономики региона при максимизации конечного потребления. Для этого мы сравним интенсивности выполнения данного конкретного способа: для способа 2 он равен 16,12, а способа 3 равен 16,10, разница хоть и небольшая, но имеется. Например, в сумме за десять периодов это будет 162,35 для первого случая и 160,37 для второго. Соответственно, в больших масштабах даже эта разница может составить значительную сумму и даст эффект в виде роста всей экономики в долгосрочной перспективе. Например, накопленный центральный бюджет будет тогда выглядеть следующим образом: с внедрением способа 2 было накоплено 104 649,6 и 79 970,49 тыс. руб., при способе 3 — разница еще более существенная (рис. 5). Таким образом, уже на основании этих результатов можно делать вывод: выгодно внедрять способ 2 производства машин.
. Остается выяснить, внедрение которого из них будет более полезным с точки зрения всей экономики региона при максимизации конечного потребления. Для этого мы сравним интенсивности выполнения данного конкретного способа: для способа 2 он равен 16,12, а способа 3 равен 16,10, разница хоть и небольшая, но имеется. Например, в сумме за десять периодов это будет 162,35 для первого случая и 160,37 для второго. Соответственно, в больших масштабах даже эта разница может составить значительную сумму и даст эффект в виде роста всей экономики в долгосрочной перспективе. Например, накопленный центральный бюджет будет тогда выглядеть следующим образом: с внедрением способа 2 было накоплено 104 649,6 и 79 970,49 тыс. руб., при способе 3 — разница еще более существенная (рис. 5). Таким образом, уже на основании этих результатов можно делать вывод: выгодно внедрять способ 2 производства машин.
А теперь представим, что правительство региона заботится не только о росте экономики и росте выпуска машин, но и о благосостоянии народа, поэтому хочет максимально увеличить оплату специалистам, работающим во всех отраслях. Соответственно, мы меняем значения вектора C: для конечного потребления мы устанавливаем значение 0, а для заработной платы по всем четырем способам ставим значение 1. Результаты задачи по максимизации заработной платы представлены в табл. 13 и 14.
Таблица 13. Интенсивность способов производства с добавлением способа 2 при максимизации заработной платы
| Период | Производство | Банк | Конечное потребление | Заработная плата | Кредиты в потребительском банке | |||||||||
| Машины (способ 1) | Машины (способ 2) | Пластик | Металл | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |||
| 1 | 1,29 | 1,00 | 0,93 | 0,91 | 3660 | 500,0 | 0,0 | 0,0 | 0,0 | 10 349 | 6000 | 4651 | 4000 | 0,0 |
| 2 | 1,31 | 0,99 | 0,92 | 0,90 | 6296 | 0,0 | 0,0 | 0,0 | 0,0 | 10 495 | 5940 | 4605 | 3960 | 0,0 |
| 3 | 1,33 | 0,98 | 0,91 | 0,89 | 1829 | 0,0 | 0,0 | 0,0 | 0,0 | 10 640 | 5881 | 4559 | 3920 | 0,0 |
| 4 | 1,32 | 0,97 | 0,90 | 0,88 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 10 585 | 5822 | 4513 | 3881 | 0,0 |
| 5 | 1,31 | 0,96 | 0,89 | 0,87 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 10 479 | 5764 | 4468 | 3842 | 0,0 |
| 6 | 1,30 | 0,95 | 0,88 | 0,86 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 10 374 | 5706 | 4423 | 3804 | 0,0 |
| 7 | 1,28 | 0,94 | 0,88 | 0,86 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 10 271 | 5649 | 4379 | 3766 | 0,0 |
| 8 | 1,27 | 0,93 | 0,87 | 0,85 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 10 168 | 5592 | 4335 | 3728 | 0,0 |
| 9 | 1,26 | 0,92 | 0,86 | 0,84 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 10 066 | 5536 | 4292 | 3691 | 0,0 |
| 10 | 1,25 | 0,91 | 0,85 | 0,83 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 99 66 | 5481 | 4249 | 3654 | 0,0 |
Таблица 14. Интенсивность способов производства с добавлением способа 3 при максимизации заработной платы
| Период | Производство | Банк | Конечное потребление | Заработная плата | Кредиты в потребительском банке | |||||||||
| Машины (способ 1) | Машины (способ 3) | Пластик | Металл | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |||
| 1 | 1,04 | 1,00 | 0,93 | 0,91 | 1020 | 0,00 | 0,00 | 0,00 | 0,00 | 8349 | 8000 | 4651 | 4000 | 0,00 |
| 2 | 1,06 | 0,99 | 0,92 | 0,90 | 3017 | 0,00 | 0,00 | 0,00 | 0,00 | 8515 | 7920 | 4605 | 3960 | 0,00 |
| 3 | 1,34 | 0,98 | 0,71 | 0,67 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 10 692 | 7841 | 3530 | 2937 | 0,00 |
| 4 | 1,32 | 0,97 | 0,74 | 0,67 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 10 585 | 7762 | 3724 | 2929 | 0,00 |
| 5 | 1,31 | 0,96 | 0,78 | 0,66 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 10 479 | 7685 | 3915 | 2921 | 0,00 |
| 6 | 1,30 | 0,95 | 0,82 | 0,66 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 10 374 | 7608 | 4105 | 2913 | 0,00 |
| 7 | 1,28 | 0,94 | 0,86 | 0,66 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 10 271 | 7532 | 4293 | 2905 | 0,00 |
| 8 | 1,27 | 0,93 | 0,87 | 0,69 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 10 168 | 7457 | 4335 | 3040 | 0,00 |
| 9 | 1,26 | 0,92 | 0,86 | 0,74 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 10 066 | 7382 | 4292 | 3260 | 0,00 |
| 10 | 1,25 | 0,91 | 0,85 | 0,79 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 9966 | 7308 | 4249 | 3477 | 0,00 |
Мы видим, что способы 2 и 3 выполняются одинаково интенсивно на протяжении всех периодов. Но нам (в данном случае — заинтересованным в увеличении благосостояния населения) важно узнать, на сколько увеличилось благосостояние. Для этого сравним суммарную интенсивность способов производства 2 и 3 по выплате заработной платы на всех четырех предприятий за десять периодов. В первом эксперименте мы получаем 243 485 тыс. руб., во втором — 250 000 тыс. руб., соответственно, внедрение способа 3 дает набольший эффект в росте заработных плат.
Таким образом, мы увидели, как в зависимости от выбранного критерия оптимальности различные экономические проекты могут оказаться более или менее полезными для экономики. В нашем примере проект 2 производства машин был более эффективным, если бы наша цель состояла в увеличении конечного потребления и росте накоплений бюджета. С другой стороны, если цель руководства региона — рост заработных плат, то проект 3 дает лучшие результаты.
Здесь мы рассмотрели только некоторые варианты применения критерия оптимальности, хотя их может быть множество. Например, если бы руководство региона было заинтересовано в увеличении прибыли отдельного предприятия, то критерий оптимальности, и, соответственно, результат решения задачи, т.е. интенсивности всех способов производства, были бы другими.
7. Заключение
Описанный в работе метод компьютерной оценки эффективности проектов может быть использован в работе упомянутых ранее сетей ситуационных центров. Варианты взаимодействия между такими ситуационными центрами, руководством регионов и работающих в нем предприятий могут быть различными.
Например, руководство предприятия предлагает проект модернизации своего предприятия и просит региональные власти помочь в финансировании. Предлагаемый метод оценки эффективности проектов позволяет получить всю палитру вариантов и провести их сравнение по критериям оптимальности, кредитным ставкам, ценовой и потребительской политике. Для расчетов ситуационный центр должен получить информацию о предприятии, предлагаемых проектах модернизации, а также финансовой ситуации в стране и регионе.
Мы еще раз обращаем внимание читателя на то, что приведенные в работе условные числовые примеры были использованы с целью демонстрации возможностей предложенной нами системы. Также хотим отметить, что разработанная система и возможности программной среды Wolfram Mathematica позволяют производить расчеты матриц любой размерности. Число как продуктов (параметров), так и самих проектов может быть значительно расширено в зависимости от поставленных целей.
Применение данной системы для расчетов и оценки экономических проектов для реальных проектов с использованием таблиц межотраслевого баланса планируется осветить в будущих работах авторов.
=== Подрисуночные подписи к статье: СИСТЕМА ОЦЕНКИ ПРОЕКТОВ НА ОСНОВЕ КОМБИНИРОВАННЫХ МЕТОДОВ КОМПЬЮТЕРНОЙ ОПТИМИЗАЦИИ В.Л. Макаров, Б.А. Ахмадеев
Рис. 1. Алгоритм возврата кредитных денег в бюджет:  — сумма возвращаемого кредита, включая проценты;
— сумма возвращаемого кредита, включая проценты;  — кредитная ставка (в долях);
— кредитная ставка (в долях);  — сумма взятого у ЦБ кредита;
— сумма взятого у ЦБ кредита;  — баланс предприятия 1 в период
— баланс предприятия 1 в период  . Рис. 2. Значение ROI на накопленные инвестиции и накопленный возврат за 50 периодов моделирования Рис. 3. Трехмерное представление результатов эксперимента при критерии полезности «уровень накопления бюджета» Рис. 4. Трехмерное представление результатов эксперимента при критерии полезности «уровень накопления конечного потребления» Рис. 5. Накопленный центральный бюджет за десять периодов, тыс. руб.
. Рис. 2. Значение ROI на накопленные инвестиции и накопленный возврат за 50 периодов моделирования Рис. 3. Трехмерное представление результатов эксперимента при критерии полезности «уровень накопления бюджета» Рис. 4. Трехмерное представление результатов эксперимента при критерии полезности «уровень накопления конечного потребления» Рис. 5. Накопленный центральный бюджет за десять периодов, тыс. руб.
Рис. 1 к статье Макаров, Ахмадеев Экономика и мат. методы № 4-2018 г.
Рис. 2 к статье Макаров, Ахмадеев Экономика и мат. методы № 4-2018 г. [[[image49]]] Рис. 3 к статье Макаров, Ахмадеев Экономика и мат. методы № 4-2018 г.
Рис. 4 к статье Макаров, Ахмадеев Экономика и мат. методы № 4-2018 г.
Рис. 5 к статье Макаров, Ахмадеев Экономика и мат. методы № 4-2018 г.
References
- 1. Akhmadeev B., Manakhov S. (2015) Effective and Sustainable Cooperation between Start-ups, Venture Investors, and Corporations. Journal of Security and Sustainability, 5 (2), 269285. DOI: http://dx.doi.org/10.9770/jssi.2015.5.2 (12).
- 2. Arrow K., Debreu G. (1954). Existence of Equilibrium for a Competitive Economy. Econo-metrica, 25, 265290.
- 3. Bernanke B., Gertler M. (1995). Inside the Black Box: The Credit Channel of Monetary Policy Transmission. Journal of Economic Perspectives, 9 (4), 2748.
- 4. Blanchard O.J., Fischer S. (1989). Lectures on Macroeconomics. Cambridge: MIT Press.
- 5. Dawid H. (2006). Agent-Based Models of Innovation and Technological Change. Handbook Computational Economics, 2, 12351272 (ISSN 15740021).
- 6. Delli Gatti D., Guilmi C., Gaffeo E., Giulioni G., Gallegati M., Palestrini A. (2005). A New Approach to Business Fluctuations: Heterogeneous Interacting Agents, Scaling Laws and Fi-nancial Fragility. Journal of Economic Behaviour Organization, 56 (4), 489512.
- 7. Kantorovich L.V. (1959). Economic Calculation of the Best Use of Resources. Moscow: Publishing House of the USSR Academy of Sciences (in Russian).
- 8. Kantorovich L.V., Bogachev V.N., Makarov V.L. (1970). About an Estimation of Efficien-cy of Capital Expenses. Economics and Math. Methods, 6, 6, 811826 (in Russian).
- 9. Kutschinski E., Uthmann T., Polani D. (2003). Learning Competitive Pricing Strategies by Multi-Agent Reinforcement Learning. Journal of Economic Dynamics Control, 27, 22072218.
- 10. LeBaron B. (2006). Agent-Based Financial Markets: Matching Stylized Facts with Style. In: Colander D. (ed.) Post-Walrasian macroeconomics. New York: Cambridge University Press. P. 221235.
- 11. Makarov V.L., Bakhtizin A.R. (2013). Social Modeling a New Computer Breakthrough (Agent-Based Models). Moscow: Economics (in Russian).
- 12. Moiseev N., Akhmadeev Bulat A. (2017). Agent-Based Simulation of Wealth, Capital and Asset Distribution on Stock Markets. Journal of Interdisciplinary Economics, May. DOI: 10.1177/0260107917698781.
- 13. Raberto M., Cincotti S., Focardi S., Marchesi M. (2001). Agent-based simulation of a fi-nancial market. Physica A: Statistical Mechanics and its Applications, 299, (1), 319327.
- 14. Ramsey F.P. (1929). On a Problem in Formal Logic. Proc. London Math. Soc., 30, 264286. doi:10.1112/plms/s2-30.1.264.
- 15. Samuelson P. (1958). An Exact Consumption-Loan Model of Interest with or without the Social Contrivance of Money. J. of Political Economy, 66, 6, 467482.
- 16. Shapiro C., Stiglitz J. (1984). Equilibrium Unemployment as a Discipline Device. American Economic Review, 74 (3), 433444.
- 17. Tassier T., Menczer F. (2001). Emerging Small-World Referral Networks in Evolutionary Labor Markets. IEEE Transactions, Evolutionary Computation, 5 (5), 482292.
- 18. Tobin J. (1969). A General Equilibrium Approach to Monetary Theory. J. of Money, Credit, and Banking, 1, 1529.
![Рис. 2 к статье Макаров, Ахмадеев Экономика и мат. методы № 4-2018 г. [[[image49]]] Рис. 3 к статье Макаров, Ахмадеев Экономика и мат. методы № 4-2018 г. Рис. 2 к статье Макаров, Ахмадеев Экономика и мат. методы № 4-2018 г. [[[image49]]] Рис. 3 к статье Макаров, Ахмадеев Экономика и мат. методы № 4-2018 г.](https://api.selcdn.ru/v1/SEL_83924/images/publication_images/4998/image48.png)