1. ВВЕДЕНИЕ

Напомним, что геометрической медианой конечного набора точек, расположенных в евклидовом пространстве Rn , называется точка m∈Rn , суммарное расстояние от которой до точек набора минимально, т.е.

m=arg minX∈Rn∑i=1kPi-X. (1)

Первая задача о геометрической медиане была сформулирована Пьером Ферма в 1643 г. для случая n=2, k=3, она была решена Еванджелиста Торричелли в 1646 г. (Fermat–Torricelli problem, 2019). При n=1 , когда мы имеем дело с набором чисел P1, ..., Pk , нетрудно проверить, что статистическая медиана m этого набора (выборки) удовлетворяет соотношению (1).

Геометрическая медиана и ее непосредственные обобщения активно использовались экономистами в теории размещения производства, начиная с XIX в. (Launhardt, 1882; Weber, 1909; Weber problem, 2012). Параллельно с экономическими приложениями проводились математические исследования свойств геометрической медианы конечных наборов точек и разрабатывались эффективные численные методы для ее нахождения (Wesolowsky, 1993). Ближе к нашему времени интерес исследователей смещается в сторону непрерывного случая — развиваются исследования, связанные с геометрическими медианами кривых и областей (Fekete, Mitchell, Beurer, 2005; Zhang, Carlsson, 2014; Savvateev, Sorokin, Weber, 2015; Панов 2017).

После этого краткого исторического экскурса дадим необходимые определения и коротко опишем основные результаты настоящей работы, являющиеся обобщением некоторых результатов, изложенных в статье (Панов, 2018). По аналогии с определением (1), геометрическая медиана ограниченной области Ω , расположенной в евклидовом пространстве Rn , определяется как точка m , являющаяся решением минимизационной задачи

m=arg minX∈Rn∫P∈ΩP-XdP, (2)

где P-X — обычное евклидово расстояние между точками X и P . Таким образом, геометрическая медиана — это точка в Rn , которая минимизирует суммарное расстояние от себя до всех точек области Ω (Fekete, Mitchell, Beurer, 2005; Savvateev, Sorokin, Weber, 2015). Существуют эффективные численные, в том числе градиентные, методы отыскания геометрической медианы (Zhang, Carlsson, 2014). В то же время общие аналитические формулы для ее вычисления отсутствуют.

Известно, что при n>1 для любой ограниченной области Ω в Rn геометрическая медиана существует и она единственна (Kemperman, 1987). Таким образом, при n>1 медиана совпадает с единственной точкой X∈Rn , которая является решением градиентного уравнения ∇X∫P∈ΩP-XdP=0. В силу векторной природы данное уравнение называют градиентной системой. А так как ∇XP-X=X-P/P-X, эту градиентную систему можно записать и в виде

∫P∈ΩX-PP-XdP=0. (3)

Мы предлагаем использовать для вычисления геометрической медианы другую, в некоторых случаях более удобную, форму записи градиентной системы (3), которая по крайней мере снижает кратность интеграла, необходимого для составления этой системы:

∫P∈∂ΩP-Xn→PdP=0, (4)

где Ω — это ограниченная область с кусочно-гладкой границей, n→P — единичный нормальный вектор к границе ∂Ω в точке P .

Доказательство того, что геометрическая медиана является решением этого уравнения (теорема 3), — один из главных результатов настоящей работы. Мы продемонстрируем здесь индуктивный геометрический подход к доказательству этого утверждения, начиная с плоского случая и с треугольных и многоугольных областей. Затем мы обсудим распространение этого результата на другие медианоподобные точки, часто используемые в экономических исследованиях.

Пусть f — непрерывная функция аргумента P∈Rn . Для области Ω рассмотрим минимизационную задачу

mf=arg minX∈Rn∫P∈ΩfP-XdP. (5)

Оказывается, здесь работают те же аргументы, что и в случае геометрической медианы. Можно доказать (см. теорему 4), что точка mf является одним из решений уравнения ∫P∈∂ΩfP-Xn→PdP=0. В дальнейшем нам будет удобно использовать другую запись определений (2) и (5). Поэтому для заданной области Ω введем в рассмотрение функцию

ΣΩX=∫P∈ΩP-XdP (6)

и определим геометрическую медиану области Ω , как

m=arg minX∈RnΣΩX. (7)

Аналогично, положим ΣΩfX=∫P∈ΩfP-XdP, тогда можно записать

mf=arg minX∈RnΣΩfX. (8)

Приведем здесь несколько примеров, показывающих необходимость рассмотрения обобщенной оптимизационной задачи (5). Во-первых, в случае fP=P решением этой задачи будет геометрическая медиана области Ω . Далее, для fP=P2 , как в этом нетрудно убедиться, в качестве решения задачи (8) мы получаем центроид области Ω , т.е. ее центр масс. Кроме того в экономических исследованиях часто используется манхэттенское расстояние, соответствующее fP=∑i=1nPi , а также и другие метрики Минковского, соответствующие fP=∑i=1nPip1/p, для которых задача (8) тоже актуальна.

2. ГЕОМЕТРИЧЕСКАЯ МЕДИАНА ТРЕУГОЛЬНОЙ ОБЛАСТИ

В этом разделе мы обсудим свойства геометрической медианы простейшей двумерной, а именно треугольной, области. Треугольную область будем обозначать Δ , а ее вершины – P1, P2, P3 . Согласно определению (7) геометрическая медиана Δ вычисляется как m=arg minX∈R2ΣΔX, где ΣΔX=∫P∈ΔP-XdP.

Пусть P1 и P2 — некоторые точки на плоскости, по аналогии с (6) введем обозначение ΣP1P2X=∫P∈P1P2P-XdP, где интегрирование ведется по отрезку P1P2 . Заметим, что среднее расстояние от точки X до точек отрезка P1P2 равно ΣP1P2X/P2-P1 .

Теорема 1. Точка m=X тогда и только тогда будет геометрической медианой треугольной области Δ с вершинами P1, P2, P3 , когда выполняется равенство

ΣP1P2XP2-P1P1P2→+ΣP2P3XP3-P2P2P3→+ΣP3P1XP1-P3P3P1→=0. (9)

Доказательство. Из определения (7) следует, что геометрическая медиана m —критическая точка функции ΣΔ . Возьмем малый вектор δ→, δ→=δ и вычислим приращение функции ΣΔ при смещении аргумента на этот вектор δΣΔX=ΣΔX+δ→-ΣΔX. В критической точке m оно должно иметь порядок oδ .

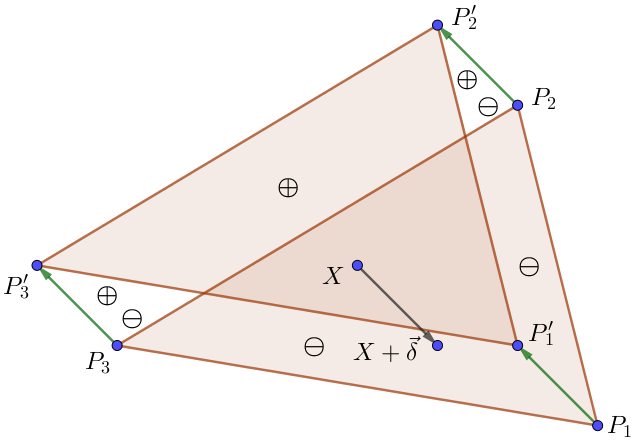
Положим P'i=Pi-δ→ и обозначим через Δ' сдвинутый на вектор -δ→ треугольник со штрихованными вершинами (рис. 1, знаки «+» и «–» соответствуют знакам, с которыми слагаемые ΣπiX входят в приращение δΣΔX ). На рис. 1 показано, что при смещении аргумента на вектор  δ→ мы можем записать приращение функции ΣΔ в виде δΣΔX=ΣΔ'X-ΣΔX.

Рис. 1. Исходный треугольник и его параллельный сдвиг

Обозначим параллелограмм с вершинами Pi, Pi+1, P'i, P'i+1 через πi , а его площадь через |πi| . Тогда приращение функции ΣΔ представляется суммой трех слагаемых вида ΣπiX , взятых с подходящими знаками. Причем при δ→0 средние значения интегралов ΣπiX и ΣPiPi+1X сближаются друг с другом, а именно:

ΣπiX|πi| =ΣPiPi+1XPi+1-Pi+o1.

Вопрос о знаке, с которым слагаемое ΣπiX должно входить в приращение δΣΔX , решается следующим образом. Умножим обе части предыдущего равенства на ориентированную площадь параллелограмма πi , а именно на -δ→∧PiPi+1→ :

-δ→∧PiPi+1→πiΣπi=-δ→∧PiPi+1→ΣPiPi+1(X)Pi+1-Pi+o(δ).

Нетрудно проверить (см. рис. 1), что дробь, стоящая перед ΣπiX , определяет искомый знак. Таким образом,

δΣΔ(X)=-δ→∧ΣP1P2(X)P2-P1P1P2→+ΣP2P3(X)P3-P2P1P2→+ΣP3P1(X)P2-P1P1P2→+o(δ). (10)

Мы видим, что приращение δΣΔX в точке X в том и только в том случае будет иметь порядок oδ , когда выражение в скобках будет равно нулю.▄

Замечание 1. На самом деле соотношение (10) говорит о том, что вектор, расположенный в скобках, — это градиент функции ΣΔX , повернутый на -90° . Так что уравнение  (9) — это всего лишь удобная запись градиентной системы ∇ΣΔX=0 для нахождения геометрической медианы треугольной области Δ .

Градиентную систему (9) можно записать в более компактном и симметричном виде, так как из теоремы 1 вытекает следующее утверждение.

Предложение 1 (характеристическое свойство геометрической медианы треугольной области). Точка m=X тогда и только тогда будет медианой треугольной области Δ с вершинами P1, P2, P3 , когда выполняется соотношение

ΣP1P2XP2-P1=ΣP2P3XP3-P2=ΣP3P1XP1-P3. (11)

Таким образом, геометрическая медиана треугольной области — это точка, для которой три средних расстояния до трех сторон граничного треугольника равны между собой.

Доказательство. В треугольнике одну из сторон выразим через две другие P3P1→=-P1P2→-P2P3→ , тогда для него равенство (10) можно переписать в виде

ΣP1P2XP2-P1-ΣP3P1XP1-P3P1P2→+ΣP2P3XP3-P2-ΣP3P1XP1-P3P2P3→=0.

Из-за независимости векторов P1P2→ и P2P3→ следует, что соответствующие им коэффициенты должны быть равны 0 и, значит, соотношение (11) в критической точке выполняется. ▄

Замечание 2. Отметим, что все интегралы вида ΣPQX , содержащиеся в градиентных системах (9) и (11), вычисляются в элементарных функциях (Zhang, Carlsson, 2014; Панов, 2018).

Сейчас мы используем доказанное здесь характеристическое свойство для точного вычисления геометрической медианы для одного очень узкого класса треугольников. Рассмотрим вырожденный случай, в котором градиентная система решается в явном виде — это случай сплюснутого треугольника. Речь идет о треугольнике со сторонами α, β, γ, в котором γ=α-β , и имеется в виду следующее утверждение, являющееся следствием предложения 1.

Следствие 1. Рассмотрим семейство треугольников со сторонами α, β, γ, , где две большие стороны α и β фиксированы, а меньшая γ — является параметром. Обозначим геометрическую медиану области, ограниченной этим треугольником mγ . Пусть теперь γ стремится к α-β , тогда mγ стремится к точке m , которая отстоит от общей вершины сторон α и β на расстояние αβ/2 .

Это утверждение является простым следствие соотношения (11), примененного непосредственно к сплюснутому треугольнику со сторонами и γ=α-β , для которого оно имеет смысл, хотя само понятие геометрической медианы для его внутренности не совсем определено по причине отсутствия этой внутренности.

Доказательство. Расположим сплюснутый треугольник, как показано это на рис. 2. Рис. 2. Сплюснутая треугольная область

Медиана m этого треугольника лежит на отрезке 0, minα, β. Для ее вычисления воспользуемся формулой (11), которая в данном случае выглядит так

1α∫0αx-mdx=1β∫0βx-mdx=1α-β∫βαx-mdx.

После вычисления интегралов получаем систему

m2+α-m2α=m2+β-m2β=α-m2+β-m2α-β,

ее решением служит m=αβ/2 , при этом значении m все три выражения равны α-2αβ+β .▄

Добавим, что среди сплюснутых треугольников имеются два типа равнобедренных — это треугольники со сторонами α, α/2, α/2 и α, α, 0 . В работе (Панов, 2018) содержится более точная, чем в следствии 1, асимптотическая информация о расположении соответствующих им геометрических медиан.

Замечание 3. Множество сплюснутых треугольных областей, для которых мы получили формулу точного местоположения геометрической медианы, пренебрежимо мало по сравнению с множеством всех треугольных областей. По-видимому, не существует простой аналитической формулы для нахождения расположения геометрической медианы треугольной области общего вида, и тем более произвольной области. Косвенно об этом можно судить по обширному списку центров треугольника, для которых известны формулы вычисления (Kimberling, 2020). Геометрическая медиана треугольной области там отсутствует.

3. ГРАДИЕНТНАЯ СИСТЕМА ДЛЯ ПРОИЗВОЛЬНОЙ ОБЛАСТИ В Rn

Здесь мы сначала закончим с двумерными областями, расположенными в R2 , а затем сформулируем основной результат, пригодный и для n-мерных областей, расположенных в Rn .

Вернемся к теореме 1, а именно к векторному уравнению (9), представляющему градиентную систему для отыскания геометрической медианы треугольной области. Глядя на это уравнение, нетрудно догадаться, как должна выглядеть градиентная система для геометрической медианы произвольной многоугольной области на плоскости.

Теорема 2. Точка m=X тогда и только тогда будет геометрической медианой односвязной многоугольной области Π с вершинами P1, ..., Pn , когда выполняется равенство

ΣP1P2XP2-P1P1P2→+…+ΣPnP1XP1-PnPnP1→=0. (12)

Доказательство этой теоремы дословно воспроизводит доказательство теоремы 2. Мы опустим его, приведем только рис. 3, отражающий данную ситуацию. Напомним, что как и в случае треугольной области, присутствующий в (12) вектор — это градиент функции ΣΠX, повернутый на -90° . Расположение точки X+δ→ в многоугольнике Π такое же, как расположение точки X в многоугольнике П´, являющемся сдвигом П на вектор -δ→ .

Рис. 3. Исходный многоугольник и его параллельный сдвиг

Из теоремы 2 вытекает следующее утверждение.

Следствие 2. Пусть задана ограниченная плоская область Ω с кусочно-гладкой границей. Точка m будет ее геометрической медианой тогда и только тогда, когда выполняется равенство

∫P∈∂ΩP-mdP→=0, (13)

где интегрирование идет по границе области Ω . При этом уравнение (13) равносильно уравнению

∫P∈∂ΩP-mn→PdP=0, (13´)

где n→P — единичный вектор внешней нормали к ∂Ω в точке P .

Набросок доказательства. Будем считать, что область Ω односвязная. Впишем в кривую ∂Ω ломаную Π , порядок точек на которой соответствует ориентации границы ∂Ω с помощью внешней нормали. Для геометрической медианы многоугольной области, ограниченной ломаной Π , запишем соотношение (12). Остается указать, что левая часть записанного соотношения будет являться интегральной суммой для интеграла, представленного в левой части соотношения (13), и после этого перейти к пределу при условии, что длины звеньев ломаной стремятся к нулю. Заметим, что при этом же условии геометрическая медиана вписанной многоугольной области будет стремиться к геометрической медиане области Ω .

Аналогичное доказательство проходит и для неодносвязной области Ω . Добавим, что для доказательства эквивалентности соотношений (13) и (13´) достаточно повернуть вектор dP→ на -90° .

Описанный подход позволяет доказать этот результат для евклидова пространства Rn любой размерности, а не только для n=2 .

Теорема 3. Пусть в евклидовом пространстве Rn задана ограниченная область Ω с кусочно-гладкой границей. Точка m будет ее геометрической медианой тогда и только тогда, когда выполняется равенство ∫P∈∂ΩP-mn→PdP=0, где интегрирование идет по границе Ω , n→P — единичный вектор внешней нормали к ∂Ω в точке P .

В следующем разделе мы приведем альтернативное доказательство более общего утверждения.

4. f -ОБОБЩЕНИЕ

Пусть задана функция f аргумента P∈Rn . По определению функции ΣΩf имеем ΣΩfX=∫P∈ΩfP-XdP . Можно сказать, что функция ΣΩfX представляет собой семейство интегралов, параметризованное точками X∈Rn . Следующее утверждение характеризует критические точки этой функции, в том числе и точку ее минимума mf .

Теорема 4. Пусть функция f непрерывна и Ω — ограниченная область в Rn с кусочно-гладкой границей. Тогда для функции ΣΩf условие критичности точки m равносильно равенству ∫P∈∂ΩfP-mn→PdP=0, где n→P — единичный вектор внешней нормали к границе области Ω в точке P .

Замечание 4. Эта теорема может быть доказана в том же стиле, что и предыдущие, но мы предъявим здесь альтернативное доказательство, немного усилив условия, налагаемые на функцию f .

Доказательство теоремы 4. Мы наметим доказательство только для случая непрерывно дифференцируемой функции f .

Так как ∇XfP-X = -∇P fP-X , условие критичности ∇ΣΩf X=0 теперь можно записать в виде ∫P∈Ω∇PfP-mdP=0. После умножения левой и правой части этого равенства на произвольный постоянный вектор δ→ получаем ∫P∈Ω∇PfP-mδ→dP=0. Под знаком интеграла здесь расположена дивергенция векторного поля, поэтому после применения n-мерного варианта формулы Гаусса–Остроградского (Divergence theorem, 2014) получаем ∫P∈∂ΩfP-mδ→ n→PdP=0. В силу произвольности δ→ имеем ∫P∈∂ΩfP-mn→PdP=0. ▄

5. ЗАКЛЮЧЕНИЕ

Добавим несколько слов о возможных обобщениях полученных результатов. Функция FX,P=P-X , с помощью которой соотношениями (6) и (7) определяется геометрическая медиана, максимально симметрична. Она инвариантна относительно параллельных переносов T , а также изотропна, то есть инвариантна относительно вращений R пространства Rn . Это означает, что FTX,TP=FX,P и FRX,RP=FX,P .

Нетрудно убедиться, что при доказательстве теоремы 3 мы воспользовались только инвариантностью P-X относительно параллельных переносов. На самом деле такой же инвариантностью обладает и любая функция вида FX,P=fP-X . Именно это обстоятельство позволило сформулировать и доказать обобщение основного результата, содержащееся в теореме 4.

Хорошо известно, что при решении любой задачи, в том числе экономической, нужно использовать имеющиеся симметрии. В качестве дополнительного примера сошлемся здесь на работу (Zhang, Carlsson, 2014), где с помощью дополнительной симметрии в явном виде вычисляется функция ΣΩ для многоугольных областей Ω .