Market’s static model for software development based on a transport problem with non-fixed time additions

Lesik, Ilya; Perevozchikov, Aleksandr

doi:10.31857/S042473880019969-4

ВВЕДЕНИЕ

В статье рассматривается задача определения оптимальных планов назначения исполнителей по работам в статической модели рынка разработки программного обеспечения (РПО) на базе транспортной задачи (ТЗ) с фиксированными добавками (ФД) по времени. В отличие от существующей ТЗ с ФД по критерию минимума стоимости (Корбут, Финкильштейн, 1969) мы предлагаем использовать минимаксный критерий, как в классической ТЗ по времени, но с временами, которые кроме фиксированных добавок могут содержать часть, пропорциональную объемам назначения, т.е. гибридную постановку ТЗ с ФД по стоимости и классической ТЗ по времени. Такие задачи возникают при ограниченности суммарного объема транспортных средств, которые приходится использовать многократно, и при наличии некоторой фиксированной добавки, возникающей с учетом задержки принятия логистических решений цифровой платформой. В существующих платформах PBS¹, LSF², NQE, I-SOFT (Ding et al., 2012), EASY³ (What is Condor? 2006), LoadLeveler⁴ (IBM Tivoli Workload Scheduler LoadLeveler, 2007) для решения транспортной задачи и ее частного случая — задачи о назначениях — рассматривается в основном статический вариант с горизонтом планирования, равным одному периоду. Поэтому в настоящей работе мы сосредоточились на ТЗ с НП по времени. Такая схема будет более общей, чем построенная на основе ЗН на УМ, поскольку предполагает наличие переменной части времени, пропорциональной объемам поставок по соответствующему маршруту.

1. PBS Works (официальный сайт компании Altair Engineering, Inc, 2006, >>>>

2. Platform LSF 7 Update 6. «An overview of new features for platform LSF administrors» (официальный сайт компании Platform Computing Corporation, 2009, >>>> platform.com/workload-management/ whotsnew_lst7u6.pdf).

3. «What is Condor?» (официальный сайт продукта Condor, 2006, >>>>

4. IBM Tivoli Workload Scheduler LoadLeveler (официальный сайт компании «Интерфейс», 2007, >>>>

Для цифровых платформ на рынке РПО частные показатели интерпретируются как цена одного дня для каждого назначения, которая может учитывать скидку на объем поставки. Таким образом, учитывается не только базовая розничная цена, но и скидка на опт. Оптимизация производится в интересах цифровой платформы, которая является как бы оптовым поставщиком и хотела бы продавать свой ресурс в розницу насколько это возможно. В результате возникает максиминная задача максимизации наименьшей цены поставки. Это позволяет учесть разницу между оптовой и розничной ценой, которая может быть для каждого назначения определена построением соответствующего линейного тренда по ретроспективным данным. Поэтому предложенная ТЗ с НД является уточнением ЗН на УМ в части разницы между оптовыми и розничными ценами.

Практическая значимость работы связана с использованием статической модели для распределения ресурсов и заданий на рынке РПО для создания соответствующих цифровых трансакционных платформ (Устюжанина, Дементьев, Евсюков, 2021). Несмотря на постоянное увеличение объема сделок, на рынке РПО отсутствуют глобальные платформы по типу указанных выше универсальных платформ распределения заданий PBS, LSF, NQE, I-SOFT, EASY, LoadLeveler. Такие платформы могли быть применены в динамическом алгоритме загрузки заданий хотя бы для получения начального плана, который в динамической модели является элементом управления. Это приводит к большому числу посредников в цепочке, ведущей от заказчика к исполнителю, что влечет уменьшение стоимости работ для исполнителя до 10 раз по сравнению со стоимостью, которую готовы были платить заказчики. Таким образом, создание цифровой платформы на рынке РПО могло бы привести к более справедливому распределению доходов и росту общественного благосостояния. Максимизация же последнего равносильна, как известно, определению глобального равновесия на рынке РПО в соответствии с теоремой нобелевского лауреата Дебре (Debreu, 1954).

В общетеоретическом плане концепция равновесия (Макаров, Рубинов, 1973) на распределенном рынке однородного товара относится к мезоэкономике (Мезоэкономика развития, 2011) и лежит в основе синтеза транспортной системы многоузлового конкурентного рынка с переменным спросом и предложением (Васин, Григорьева, Лесик, 2017, 2018; Васин, Григорьева, Цыганов, 2017).

Основным результатом работы являются исследование статической ТЗ с НД по времени. Показано, что поставленная дискретно-непрерывная задача может быть аппроксимирована сверху классической ТЗ по времени, которую можно получить и по схеме, разработанной в (Balinski, 1961). Приводится точный алгоритм метода ветвей и границ (МВГ) и модельный пример его использования. Рассматривается ε-оптимальная версия метода ветвей и границ, полученная по аналогии с решением многомерной задачи о назначениях (Корбут, Финкильштейн, 1969) и особенности ее использования.

1. ПОСТАНОВКА ТРАНСПОРТНОЙ ЗАДАЧИ С НЕФИКСИРОВАННЫМИ ДОБАВКАМИ ПО ВРЕМЕНИ

Пусть, как в обычной транспортной задаче, $i = 1, . . ., m$ — пункты производства некоторого однородного товара, $j = 1, . . ., n$ — пункты его потребления. Даны величины: $a_{i} > 0$ — объем производства в пункте производства $i$ ; $b_{j} > 0$ — объем потребления в пункте потребления $j$ , отнесенные к одному периоду времени (горизонту планирования).

Требуется составить план перевозок $x = \{x_{i j}\}$ объемов перевозок из пункта $i$ в пункт $j$ , удовлетворяющий обычным транспортным ограничениям

$x_{i j} \geq 0, \sum_{j = 1}^{n} x_{i j} = a_{i}, \sum_{i = 1}^{m} x_{i j} = b_{j}, i \in M = {1, . . ., m}, j \in N = {1, . . ., n}$ (1)

и минимизирующий общее время перевозки

$I (x) = \underset{(i, j) : x_{i j} > 0}{m a x} τ_{i j} (x_{i j}) \to i n f,$ (2)

где предполагается, что $\sum_{i = 1}^{m} a_{i} = \sum_{j = 1}^{n} b_{j}$ , а частные временные показатели под знаком максимума задаются формулами

$τ_{i j} (x_{i j}) = \{\begin{array}{l} 0, x_{i j} = 0; \\ T_{i j} + t_{i j} x_{i j} / V_{i j}, x_{i j} > 0; \end{array}$ (3)

$T_{i j}$ — постоянные затраты времени, необходимые для организации перевозки по данному маршруту; $t_{i j}$ — время перевозки за одну ездку; $V_{i j}$ — суммарный объем транспортных средств на данном маршруте; $x_{i j} / V_{i j}$ — число поездок, необходимое для перевозки объема $x_{i j}$ .

Простейшие примеры показывают, что функция связанного максимума (3) может быть разрывной (Федоров, 1979). При этом справедлива следующая лемма.

Лемма 1. Функция связанного максимума I(x) полунепрерывна снизу в допустимой области (1).

Доказательство. Пусть дана последовательность $x^{n} \to x^{0}$ и $B (x^{0}) = \{(i, j) : x_{i j}^{0} > 0\}$ , тогда для всех достаточно больших выполняются неравенства $x_{i j}^{n} > 0 \forall (i, j) \in B (x^{0}) \Rightarrow B (x^{n}) \supseteq B (x^{0}),$ откуда следует

$\underset{(i, j) \in B (x^{n})}{m a x} f_{i j} (x_{i j}) \geq \underset{(i, j) \in B (x^{0})}{m a x} f_{i j} (x_{i j}) \Rightarrow \underset{x \to \infty}{l i m} i n f I (x^{n}) \geq \underset{x \to \infty}{l i m} i n f \underset{(i, j) \in B (x^{0})}{m a x} f_{i j} (x_{i j}) = I (x^{0}) .$

Причем последнее равенство верно в силу непрерывности частных показателей.

Замечание 1. В силу доказанного утверждения инфимум в постановке задачи (1)–(3) можно заменить на минимум.

Задачу (1)–(3) назовем транспортной задачей с нефиксированными добавками (ТЗНД) по времени, в отличие от транспортной задачи с фиксированными доплатами (ТЗФД) по стоимости (Корбут, Финкильштейн, 1969).

2. АППРОКСИМАЦИЯ ЗАДАЧИ

Введение дополнительных целочисленных переменных в ТЗНД (1)–(3) по времени позволит нам свести задачу к классической ТЗ по времени. Для ТЗФД такой способ был указан в (Balinski, 1961), и он подходит для ТЗНД (1)–(3) по времени, но в нем будут присутствовать некоторые особенности. Положим $M_{i j} = m i n \{a_{i}, b_{j}\}, i = 1, . . ., m, j = 1, . . ., n .$

Рассмотрим частично-целочисленную задачу минимизации

$\underset{(i, j)}{m a x} (T_{i j} y_{i j} + t_{i j} x_{i j} / V_{i j}) \to m i n$ (4)

при условиях (1) и дополнительных условиях

$y_{i j} = 0,1; x_{i j} \leq M_{i j} y_{i j} .$ (5)

Тогда задача (1), (4), (5) эквивалентна исходной задаче (1)–(3) и может быть аппроксимирована сверху (по значению) классической ТЗ по времени:

$\underset{(i, j)}{m a x} (T_{i j} y_{i j} + t_{i j} x_{i j} / V_{i j}) \leq \underset{(i, j)}{m a x} (T_{i j} + t_{i j} M_{i j} / V_{i j}) y_{i j} = \underset{(i, j); x_{i j} > 0}{m a x} (T_{i j} + t_{i j} M_{i j} / V_{i j}) \to m i n$ (6) при условиях (1). Справедлива следующая лемма.

Лемма 2. Задача (1)–(3) аппроксимируется сверху по значению обычной транспортной задачей (1), (6) по времени.

Замечание 2. В частном случае задачи о назначениях $M_{i j} = 1$ задача (1)–(3) эквивалентна обычной ТЗ (1), (4), (7) по времени, в чем легко убедиться непосредственной проверкой.

Замечание 3. В частности, когда $a_{i} \equiv 1, b_{i} \equiv 1 (m = n),$ имеем задачу о назначениях на узкие места (Форд, Фалкерсон, 1966).

3. МЕТОД ВЕТВЕЙ И ГРАНИЦ

Для точного решения дискретно-непрерывной задачи (1)–(3) разобьем допустимое многогранное множество на непустые грани и возьмем их относительные внутренности (Сухарев, Тимохов, Федоров, 1986). Каждая такая грань получается фиксированием подмножеством $B \subset M \times N$ пар индексов $(i, j)$ , на которых соответствующие переменные удовлетворяют условиям:

$x_{i j} > 0, (i, j) \in B$ , $x_{i j} = 0, (i, j) \notin B .$ (7)

Положим

$I_{B} = \underset{x \in {\bar{X}}_{B}}{i n f} \underset{(i, j) \in B}{m a x} τ_{i j} (x_{i j}) .$ (8)

Здесь $X_{B} \subseteq X$ — подмножество допустимых решений $X$ ограничений (1), удовлетворяющих дополнительным ограничениям (7). Поскольку относительные внутренности непустых граней непусты $(X_{B} \neq ϕ)$ (Сухарев, Тимохов, Федоров, 1986, с. 65), то замыкание ${\bar{X}}_{B}$ подмножества $X_{B} \subseteq X$ получается заменой строгих неравенств (7) нестрогими (Федоров, 1979, с. 30):

$x_{i j} \geq 0, (i, j) \in B,$ $x_{i j} = 0, (i, j) \notin B,$ (9)

задача (1), (7), (8) равносильна задаче

$I_{B} = \underset{x \in {\bar{X}}_{B}}{m i n} I_{B} (x) = \underset{x \in {\bar{X}}_{B}}{m i n} \underset{(i, j) \in B}{m a x} τ_{i j} (x_{i j}) .$ (10)

Задача (1), (9), (10) является задачей выпуклого программирования, поэтому исходная задача (1)–(3) сводится к решению задач выпуклого программирования на непустых гранях. Справедлива следующая лемма.

Лемма 3. Минимальное значение $I$ общего показателя в задаче (1)–(3) получается как наименьшее значение $I_{B}$ задачи (10) по всем $B \subset M \times N$ .

Поскольку это комбинаторная задача, то в общем случае для точного решения необходимо использовать метод ветвей и границ. Узлы поискового орграфа можно отождествить с подмножествами $\bar{B} \subset M \times N$ , дополняющими множества $B$ в $M \times N$ . Ориентированной дугой связываются любые два подмножества $\bar{B'} \supseteq \bar{B''}$ , отличающихся одним элементом.

Спрашивается, как получить нижние оценки в ТЗНД по времени. Для этого можно снять все ограничения $x_{i j} = 0$ в данном узле поискового орграфа, но оставить тот же критерий с теми же функциями и в том же количестве под знаком максимума, который следует минимизировать на всем допустимом множестве $X$ . Тогда показатель не изменится, а множество расширится, в результате минимум станет меньше. Полученная задача является задачей выпуклого программирования, которая может быть решена методом Б.Т. Поляка (Поляк, 1983).

Для вычисления $I_{B}$ в узлах поискового орграфа можно снять равенства в ограничениях (9) при помощи штрафной функции (Федоров, 1979):

$L_{B} (x) = \sum_{(i, j) \in \bar{B}} x_{i j}^{2} .$ (11)

Тогда приходим к показателю

$J_{B} (x) = I_{B} (x) + C L_{B} (x)$ , (12)

который также следует минимизировать на всем допустимом множестве $X$ . Здесь $C > 0$ — достаточно большая константа.

В силу линейности частных показателей в (10) и выпуклости (11) показатель (12) представляет собой выпуклую функцию такого же типа, как при вычислении нижних оценок.

Теперь мы выясним, сколько может быть нулевых переменных $x_{i j}$ . Поскольку имеем $m n - m - n + 1 = (m - 1) (n - 1)$ независимых переменных, то нулевых переменных может быть не более $(m - 1) (n - 1)$ и размерность граней может принимать соответственно значения $0, 1, . . ., (m - 1) (n - 1) - 1$ в невырожденном случае.

4. ПРИМЕР ТОЧНОГО РЕШЕНИЯ ЗАДАЧИ

Пример 1. Предположим, что $a = (5, 4), b = (2, 4, 3)$ , а исходные матрицы имеют вид:

$T = (\begin{array}{l} \begin{array}{l} 1 & 2 & 3 \end{array} \\ \begin{array}{l} 4 & 3 & 2 \end{array} \end{array})$ , $t = (\begin{array}{l} \begin{array}{l} 3 & 2 & 5 \end{array} \\ \begin{array}{l} 2 & 4 & 5 \end{array} \end{array})$ , $V = (\begin{array}{l} \begin{array}{l} 2 & 4 & 3 \end{array} \\ \begin{array}{l} 2 & 4 & 3 \end{array} \end{array}),$ (13)

тогда

$M = (\begin{array}{l} \begin{array}{l} 2 & 4 & 3 \end{array} \\ \begin{array}{l} 2 & 4 & 3 \end{array} \end{array}) .$

Рассмотрим сначала основной случай, когда все $x_{i j} > 0$ . Тогда, исключая зависимые переменные в первом столбце и первой строке, приходим к показателю

$\begin{array}{l} I (x) = m a x \{(T_{11}^{} + t_{11}^{} \{a_{1} - (b_{2} - x_{22}) - (b_{3} - x_{23})\} / V_{11}), (T_{21}^{} + t_{21}^{} (a_{2} - x_{22} - x_{23}) / V_{21}^{}), \\ (T_{12}^{} + t_{12}^{} (b_{2} - x_{22}) / V_{12}), (T_{13}^{} + t_{13}^{} (b_{3} - x_{23}) / V_{13}), (T_{22}^{} + t_{22}^{} x_{22} / V_{22}), (T_{23}^{} + t_{23}^{} x_{23} / V_{23})\} \to m i n \end{array}$ (14)

при ограничениях

$a_{1} - (b_{2} - x_{22}) - (b_{3} - x_{23}) \geq 0, a_{2} - x_{22} - x_{23} \geq 0, b_{2} - x_{22} \geq 0, b_{3} - x_{23} \geq 0, x_{22}, x_{23} \geq 0,$

или $a_{2} \geq x_{22} + x_{23} \geq b_{2} + b_{3} - a_{1}, b_{2} \geq x_{22} \geq 0, b_{3} \geq x_{23} \geq 0,$ или с учетом значения параметров

$4 \geq x_{22} + x_{23} \geq 2, 4 \geq x_{22} \geq 0; 3 \geq x_{23} \geq 0 .$ (15)

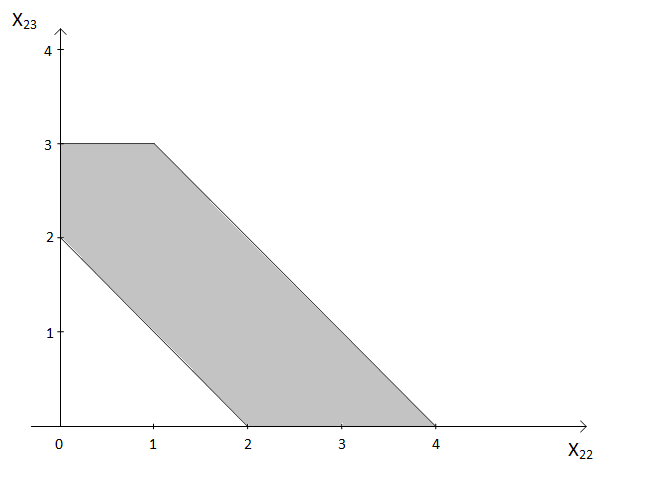
Рис. 1. Допустимая область независимых переменных в примере 1

С учетом значений параметров общий показатель (14) примет вид:

$\begin{matrix} I (x) = m a x \{[3 (x_{22} + x_{23}) / 2 - 2], [8 - x_{22} - x_{23}], \\ [4 - x_{22} / 2)], [8 - 5 x_{23} / 3], [3 + x_{22}], [2 + 5 x_{23} / 3]\} \to m i n . \end{matrix}$ (16)

Мы видим, что согласно (15) значение 4 входит в область значений всех частных показателей, стоящих под знаком максимума в (16) (рис. 1). Построим линии уровней частных показателей с этим значением, тогда из соображений, в какую сторону будут сдвигаться линии при росте значения переменных, решение задачи локализуется в конфликтной области

$4 \geq x_{22} + x_{23}, x_{22} \geq 1; 2,4 \geq x_{23} \geq 1,2 .$

Перебирая возможные варианты уравнивания соответствующих частных показателей, убеждаемся, что единственное решение соответствует системе

$\begin{array}{l} 8 - \frac{5}{3} x_{23} = 3 + x_{22} \Rightarrow \frac{10}{3} x_{23} = 6 \Rightarrow x_{23} = 1,8; \\ 2 + \frac{5}{3} x_{23} = 3 + x_{22} \Rightarrow 3 + x_{22} = 5 \Rightarrow x_{22} = 2 . \end{array}$

При этом общее значение уравненных частных показателей равно $3 + x_{22} \approx 3 + 2 = 5 .$ Не вошедший в тройку уравненных показателей частный показатель будет $8 - x_{22} - x_{23} = 8 - 3,8 = 4,2 < 5,$ следовательно, остальные частные показатели, не вошедшие в четверку конфликтующих, будут заведомо иметь значения меньше 5, что и требовалось проверить.

Замечание 4. Аналогично разбираются остальные случаи, когда какие-то $x_{i j} = 0$ . Это соответствует одномерным отрезкам границы и вершинам, т.е. 5+5=10 случаев! Согласно лемме 3 решение ТЗНД по времени сводится к ее решению на всех гранях.

Приведем соответствующие расчеты и вычислим нижние оценки в узлах поискового орграфа, необходимые в примере размера 2×3 работы МВГ, и значения критерия в полученных точках для отсева неперспективных вариантов и их наследников.

0-мерные грани

Узел 1.

$\begin{matrix} x_{22} = 4, x_{23} = 0 \Rightarrow τ_{11} = 3 (x_{22} + x_{23}) / 2 - 2 = 4; τ_{12} = 4 - x_{22} / 2 = 2; \\ τ_{13} = 8 - 5 x_{23} / 3 = 8; τ_{21} = 8 - x_{22} - x_{23} = 4; τ_{22} = 3 + x_{22} = 7; τ_{23} = 2 + 5 x_{23} / 3 = 2; \\ x_{11} = x_{22} + x_{23} - 2 = 2; x_{12} = 4 - x_{22} = 0; x_{13} = 3 - x_{23} = 3; x_{21} = 4 - x_{22} - x_{23} = 0; \\ x_{22} = 4; x_{23} = 0 \Rightarrow m a x (4,8, 7) = 8 > 5 . \end{matrix}$

Нижняя оценка получается в результате решения задачи

$m a x (3 (x_{22} + x_{23}) / 2 - 2, 8 - 5 x_{23} / 3, 3 + x_{22}) \to m i n .$ (17)

Здесь минимум берется по всей допустимой области значений переменных. Минимум достигается на прямой $8 - 5 x_{23} / 3 = 3 + x_{22} \Leftrightarrow x_{22} + 5 x_{23} / 3 = 5$ , когда общее значение $3 + x_{22}$ минимально, т.е. при $x_{22} = 0 \Rightarrow x_{23} = 3$ , когда $3 + x_{22} = 3$ . Это и есть минимальное значение показателя в задаче (17), равное нижней оценке в узле 1.

Точка, в которой достигается нижняя оценка, имеет два нуля $x_{22}, x_{13} = 0$ , поэтому значение критерия равно максимуму показателей для других переменных $m a x (2,5; 4; 5; 7) = 7$ .

Узел 2.

$\begin{array}{l} x_{22} = 2, x_{23} = 0 \Rightarrow \\ τ_{11} = 1,5 (x_{22} + x_{23}) - 2 = 1; τ_{12} = 4 - 0,5 x_{22} = 3; τ_{13} = 8 - 5 x_{23} / 3 = 8; \\ τ_{21} = 8 - x_{22} - x_{23} = 6; τ_{22} = 3 + x_{22} = 5; τ_{23} = 2 + 5 x_{23} / 3 = 2; \\ x_{11} = x_{22} + x_{23} - 2 = 0; x_{12} = 4 - x_{22} = 2; x_{13} = 3 - x_{23} = 3; \\ x_{21} = 4 - x_{22} - x_{23} = 0; x_{22} = 2; x_{23} = 0; \\ \Rightarrow m a x (3,8, 6,5) = 8 > 5 . \end{array}$

Нижняя оценка получается в результате решения задачи

$m a x (4 - x_{22} / 2, 8 - 5 x_{23} / 3, 8 - x_{22} - x_{23}, 3 + x_{22}) \to m i n .$ (18)

Здесь минимум берется по всей допустимой области значений переменных. Перебирая возможные варианты уравнивания соответствующих частных показателей, убеждаемся, что единственное решение соответствует системе

$\begin{array}{l} 8 - 5 x_{23} / 3 = 8 - x_{22} - x_{23} \Rightarrow x_{22} = 5 - 5 x_{23} / 3 = 75 / 21 = 1,429; \\ 3 + x_{22} = 8 - x_{22} - x_{23} \Rightarrow 2 x_{22} + x_{23} = 5 \Rightarrow x_{23} = 15 / 7 \approx 2,143 . \end{array}$

При этом общее значение уравненных частных показателей равно $8 - x_{22} - x_{23} \approx 4,429,$ не вошедший в тройку уравненных показателей (18) — $4 - x_{22} / 2 \approx 3,285 < 4,429 .$ Значит, остальные частные показатели будут заведомо меньше $4,429$ , что и требовалось проверить. Это и есть минимальное значение показателя в задаче (18), равное нижней оценке в узле 2.

Точка, в которой достигается нижняя оценка, не имеет нулей $x_{i j}$ , поэтому значение критерия равно максимуму показателей для всех переменных $m a x (3,358; 3,286; 4,428; 4,428; 4,428; 5,572) = 5,572$ .

Узел 3.

$\begin{matrix} x_{22} = 0, x_{23} = 2 \Rightarrow τ_{11} = 3 (x_{22} + x_{23}) / 2 - 2 = 1; τ_{12} = 4 - x_{22} / 2 = 4; τ_{13} = 8 - 5 x_{23} / 3 = 14 / 3; \\ τ_{21} = 8 - x_{22} - x_{23} = 6; τ_{22} = 3 + x_{22} = 3; τ_{23} = 2 + 5 x_{23} / 3 = 16 / 3; x_{11} = x_{22} + x_{23} - 2 = 0; \\ x_{12} = 4 - x_{22} = 4; x_{13} = 3 - x_{23} = 1; x_{21} = 4 - x_{22} - x_{23} = 2; x_{22} = 0; x_{23} = 2 \Rightarrow \\ m a x (4, 14 / 3, 6, 16 / 3) = 6 > 5 . \end{matrix}$

Нижняя оценка получается в результате решения задачи

$m a x (4 - x_{22} / 2, 8 - 5 x_{23} / 3, 8 - x_{22} - x_{23}, 2 + 5 x_{23} / 3) \to m i n .$ (19)

Здесь минимум берется по всей допустимой области значений переменных. Перебирая возможные варианты уравнивания соответствующих частных показателей, убеждаемся, что единственное решение соответствует системе

$\begin{array}{l} 8 - 5 x_{23} / 3 = 8 - x_{22} - x_{23} \Rightarrow x_{23} = 18 / 10 = 1,8; \\ 2 + 5 x_{23} / 3 = 8 - x_{22} - x_{23} \Rightarrow 8 - x_{22} - x_{23} = 5 \Rightarrow x_{22} = 1,2 . \end{array}$

При этом общее значение уравненных частных показателей равно $8 - x_{22} - x_{23} = 5,$ не вошедший в тройку уравненных показателей (19) — $4 - 0,5 x_{22} = 3,4 < 5 .$ Значит, остальные частные показатели будут заведомо меньше 5, что и требовалось проверить. Это и есть минимальное значение показателя в задаче (19), равное нижней оценке в узле 3.

Точка, в которой достигается нижняя оценка, не имеет нулей $x_{i j}$ , поэтому значение критерия равно максимуму показателей для всех переменных $m a x (2,25; 3,4; 5; 5; 4,2; 5) = 5$ . Узел 4.

$\begin{matrix} x_{22} = 0, x_{23} = 3 \Rightarrow τ_{11} = 3 (x_{22} + x_{23}) / 2 - 2 = 5 / 2; τ_{12} = 4 - x_{22} / 2 = 4; τ_{13} = 8 - 5 x_{23} / 3 = 3; \\ τ_{21} = 8 - x_{22} - x_{23} = 5; τ_{22} = 3 + x_{22} = 3; τ_{23} = 2 + 5 x_{23} / 3 = 7; x_{11} = x_{22} + x_{23} - 2 = 1; \\ x_{12} = 4 - x_{22} = 4; x_{13} = 3 - x_{23} = 0; x_{21} = 4 - x_{22} - x_{23} = 1; x_{22} = 0; x_{23} = 3 \Rightarrow \\ m a x (5 / 2, 4, 5, 7) = 7 > 5 . \end{matrix}$

Нижняя оценка получается в результате решения задачи

$m a x (3 (x_{22} + x_{23}) / 2 - 2, 4 - x_{22} / 2, 8 - x_{22} - x_{23}, 2 + 5 x_{23} / 3) \to m i n .$ (20)

Здесь минимум берется по всей допустимой области значений переменных. Минимум достигается на прямой $8 - x_{22} - x_{23} = 2 + 5 x_{23} / 3 \Leftrightarrow x_{22} + 8 x_{23} / 3 = 6$ , когда общее значение $2 + 5 x_{23} / 3$ минимально, т.е. при $x_{23} = 1,2$ , когда $x_{22} = 2,8$ и $2 + 5 x_{23} / 3 = 4$ . Это и есть минимальное значение показателя в задаче (20), равное нижней оценке в узле 4.

Точка, в которой достигается нижняя оценка, не имеет нулей $x_{i j}$ , поэтому значение критерия равно максимуму показателей для всех переменных $m a x (4; 2,6; 6; 4; 5,8; 4) = 6$ .

Узел 5.

$\begin{matrix} x_{22} = 1, x_{23} = 3 \Rightarrow τ_{11} = 3 (x_{22} + x_{23}) / 2 - 2 = 4; τ_{12} = 4 - x_{22} / 2 = 7 / 2; τ_{13} = 8 - 5 x_{23} / 3 = 3; \\ τ_{21} = 8 - x_{22} - x_{23} = 4; τ_{22} = 3 + x_{22} = 4; τ_{23} = 2 + 5 x_{23} / 3 = 7; x_{11} = x_{22} + x_{23} - 2 = 2; \\ x_{12} = 4 - x_{22} = 3; x_{13} = 3 - x_{23} = 0; x_{21} = 4 - x_{22} - x_{23} = 0; x_{22} = 1; x_{23} = 3 \Rightarrow \\ m a x (4, 7 / 2, 4, 7) = 7 > 5 . \end{matrix}$

Нижняя оценка получается в результате решения задачи

$m a x (3 (x_{22} + x_{23}) / 2 - 2, 4 - x_{22} / 2, 3 + x_{22}, 2 + 5 x_{23} / 3) \to m i n .$ (21)

Здесь минимум берется по всей допустимой области значений переменных. Минимум достигается на прямой $3 + x_{22} = 2 + 5 x_{23} / 3 \Leftrightarrow x_{22} = 5 x_{23} / 3 - 1$ , когда общее значение $3 + x_{22}$ минимально, когда $x_{22} + x_{23} = 2$ , откуда $8 x_{23} / 3 = 3$ $\Rightarrow x_{23} = 9 / 8 = 1,125$ $\Rightarrow x_{22} = 2 - x_{23} = 0,875$ и $3 + x_{22} = 3,875$ . Это и есть минимальное значение показателя в задаче (21), равное нижней оценке в узле 5. При этом $4 - x_{22} / 3 \approx 3,562 < 3,875$ , что и требовалось проверить.

Точка, в которой достигается нижняя оценка, имеет два нуля $x_{13} = 0$ , поэтому значение критерия равно максимуму показателей для других переменных $m a x (4; 3,5; 4; 4; 7) = 7$ .

1-мерные грани

Узел 6.

$\begin{matrix} 2 < x_{22} < 4, x_{23} = 0 \Rightarrow τ_{11} = 3 (x_{22} + x_{23}) / 2 - 2 < 4; τ_{12} = 4 - x_{22} / 2 < 3; τ_{13} = 8 - 5 x_{23} / 3 = 8; \\ τ_{21} = 8 - x_{22} - x_{23} < 6; τ_{22} = 3 + x_{22} < 7; τ_{23} = 2 + 5 x_{23} / 3 = 2; x_{11} = x_{22} + x_{23} - 2 = x_{22} - > 0; \\ x_{12} = 4 - x_{22} > 0; x_{13} = 3 - x_{23} = 3; x_{21} = 4 - x_{22} - x_{23} = 4 - x_{22} > 0; x_{22} > 2; x_{23} = 0; \Rightarrow \\ m a x (4, 3, 8, 6, 7, 8) = 8 > 5 . \end{matrix}$

Нижняя оценка:

$m a x (3 (x_{22} + x_{23}) / 2 - 2, 4 - x_{22} / 2, 8 - 5 x_{23} / 3, 8 - x_{22} - x_{23}, 3 + x_{22}) \to m i n,$ (22)

минимум берется по всей допустимой области значений переменных. Перебирая возможные варианты уравнивания соответствующих частных показателей, убеждаемся, что единственное решение соответствует системе

$\begin{matrix} 8 - 5 x_{23} / 3 = 8 - x_{22} - x_{23} \Rightarrow x_{22} = 5 - 5 x_{23} / 3 = 75 / 21 = 1,429; \\ 3 + x_{22} = 8 - x_{22} - x_{23} \Rightarrow 2 x_{22} + x_{23} = 5 \Rightarrow x_{23} = 15 / 7 \approx 2,143 . \end{matrix}$

При этом общее значение уравненных частных показателей равно $8 - x_{22} - x_{23} \approx 4,429,$

а не вошедшие в тройку уравненных показателей (22)

$3 (x_{22} + x_{23}) / 2 - 2 \approx 3,358 < 4,429,4 - x_{22} / 2 \approx 3,285 < 4,429 .$

Значит, остальные частные показатели будут заведомо меньше $4,429$ , что и требовалось проверить. Это и есть минимальное значение показателя в задаче (22), равное нижней оценке в узле 6.

Точка, в которой достигается нижняя оценка, не имеет нулей $x_{i j}$ , поэтому значение критерия равно максимуму показателей для всех переменных $m a x (3,358; 3,286; 4,428; 4,428; 4,428; 5,572) = 5,572$ , как в вершине 2.

Узел 7.

$\begin{matrix} x_{22}, x_{23} > 0, x_{22} + x_{23} = 2 \Rightarrow τ_{11} = 3 (x_{22} + x_{23}) / 2 - 2 = 1; τ_{12} = 4 - x_{22} / 2 < 4; \\ 14 / 3 < τ_{13} = 8 - 5 x_{23} / 3 < 8; τ_{21} = 8 - x_{22} - x_{23} = 6; 3 < τ_{22} = 3 + x_{22} < 5; \\ 2 < τ_{23} = 2 + 5 x_{23} / 3 < 16 / 3; x_{11} = x_{22} + x_{23} - 2 = 0; x_{12} = 4 - x_{22} > 2; x_{13} = 3 - x_{23} > 1; \\ x_{21} = 4 - x_{22} - x_{23} = 2; x_{22} > 0; x_{23} > 0; \Rightarrow m a x (6,8 - 5 x_{23} / 3) \to i n f, \\ 0 < x_{23} < 2 \Rightarrow 6 = 8 - 5 x_{23} / 3, x_{23} = 6 / 5 \Rightarrow m a x = 6 > 5 . \end{matrix}$

Нижняя оценка

$m a x (4 - x_{22} / 2, 8 - 5 x_{23} / 3, 8 - x_{22} - x_{23}, 3 + x_{22}, 2 + 5 x_{23} / 3) \to m i n$ (23)

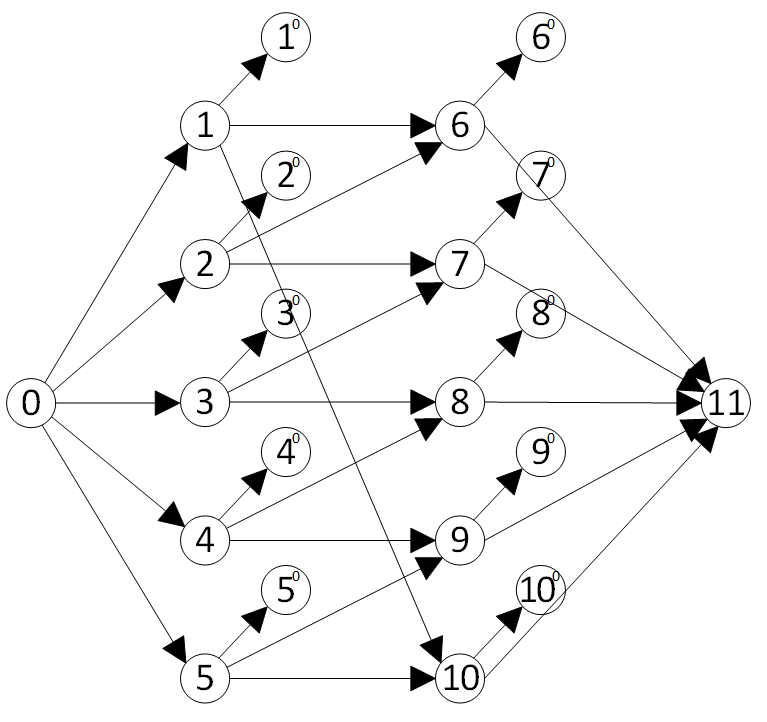
равна 5. Это показывается так же, как в основном случае, когда все переменные положительны. Основной случай обозначим узлом 11, чтобы в построенном орграфе дуги вели от вершин с меньшими номерами к большим. Введем еще начальный узел (узел 0), с которым соединим узлы 1–5. Кроме того, каждый узел соединим с терминальным узлом такого же номера, но пометим их индексом «0» и будем приписывать им значения терминального узла в случае его раскрытия, т.е. получения всех непосредственно следующих за ним узлов поискового орграфа (рис. 2).

Рис. 2. Поисковый орграф в примере 1

Перебирая возможные варианты уравнивания соответствующих частных показателей, убеждаемся, как в основном варианте, что имеется только единственное решение $x_{23} = 1,8; x_{22} = 2$ . При этом общее значение уравненных частных показателей равно 5. Значит, остальные частные показатели, не вошедшие в четверку конфликтующих, будут заведомо меньше 5, что и требовалось проверить.

Узел 8.

$\begin{matrix} (x_{22} + x_{23}) - 2 < 7 / 2; τ_{12} = 4 - x_{22} / 2 = 4; 3 < τ_{13} = 8 - 5 x_{23} / 3 = 14 / 3 < 5; \\ τ_{21} = 8 - x_{22} - x_{23} < 6; τ_{22} = 3 + x_{22} = 3; 16 / 3 < τ_{23} = 2 + 5 x_{23} / 3 < 7; x_{11} = x_{22} + x_{23} - 2 > 0; \\ x_{12} = 4 - x_{22} = 4; x_{13} = 3 - x_{23} > 0; x_{21} = 4 - x_{22} - x_{23} > 0; x_{22} = 0; x_{23} > 2 \Rightarrow \\ m a x (8 - x_{23}, 2 + 5 x_{23} / 3) \to i n f, 2 < x_{23} < 3 \Rightarrow 8 - x_{23} = 2 + 5 x_{23} / 3, x_{23} = 18 / 8 \Rightarrow \\ i n f = 8 - x_{23} = 5,75 > 5 . \end{matrix}$

Нижняя оценка:

$m a x (3 (x_{22} + x_{23}) / 2 - 2, 4 - / 2 x_{22}, 8 - 5 x_{23} / 3, 8 - x_{22} - x_{23}, 2 + 5 x_{23} / 3) \to m i n,$ (24)

минимум берется по всей допустимой области значений переменных. Перебирая возможные варианты уравнивания соответствующих частных показателей, убеждаемся, как и в вершине 2, что единственное решение соответствует системе

$\begin{array}{l} 8 - 5 x_{23} / 3 = 8 - x_{22} - x_{23} \Rightarrow 6 = 10 x_{23} / 3 \Rightarrow x_{23} = 18 / 10 = 1,8; \\ 2 + 5 x_{23} / 3 = 8 - x_{22} - x_{23} \Rightarrow x_{22} + 8 x_{23} / 3 = 6 \Rightarrow x_{22} = 1,2 . \end{array}$

При этом общее значение уравненных частных показателей равно $8 - x_{22} - x_{23} = 5,$ а не вошедшие в тройку уравненных показателей (24) будут

$3 (x_{22} + x_{23}) / 2 - 2 = 2,5 < 5; 4 - x_{22} / 2 = 3,6 < 5 .$

Значит, остальные частные показатели, не вошедшие в четверку конфликтующих, будут заведомо меньше 5, что и требовалось проверить. Это и есть значение минимальное показателя в задаче (24), равное нижней оценке в узле 8.

Точка, в которой достигается нижняя оценка, не имеет нулей $x_{i j}$ , поэтому значение критерия, как в вершине 3, равно максимуму показателей для всех переменных $m a x (2,25; 3,4; 5; 5; 4,2; 5) = 5$ .

Узел 9.

$\begin{matrix} x_{22} = 3, 0 < x_{23} < 1 \Rightarrow τ_{11} = 3 (x_{22} + x_{23}) / 2 - 2 < 4; τ_{12} = 4 - x_{22} / 2 = 2,5; \\ τ_{13} = 8 - 5 x_{23} / 3 > 6 / 3; τ_{21} = 8 - x_{22} - x_{23} < 5; τ_{22} = 3 + x_{22} = 6; τ_{23} = 2 + 5 x_{23} / 3 < 6 / 3; \\ x_{11} = x_{22} + x_{23} - 2 > 1; x_{12} = 4 - x_{22} = 1; x_{13} = 3 - x_{23} > 2; x_{21} = 4 - x_{22} - x_{23} > 0; \\ x_{22} = 3; 0 < x_{23} < 1; \Rightarrow m a x (8 - 5 x_{23} / 3) \to i n f, 0 < x_{23} < 1 \Rightarrow i n f = 6 / 3 > 5 . \end{matrix}$

Нижняя оценка:

$m a x (3 (x_{22} + x_{23}) / 2 - 2, 4 - x_{22} / 2, 8 - 5 x_{23} / 3, 8 - x_{22} - x_{23}, 3 + x_{22}, 2 + 5 x_{23} / 3) \to m i n .$ (25)

Минимум берется по всей допустимой области значений переменных. Это совпадает с основным случаем 11. Поэтому нижняя оценка в вершине 9, совпадающая с минимумом в (25), равна 5. Перебирая возможные варианты уравнивания соответствующих частных показателей, убеждаемся, как в основном варианте, что единственное решение $x_{23} = 1,8;$ $x_{22} = 2$ . При этом общее значение уравненных частных показателей равно 5. Значит, остальные частные показатели, не вошедшие в четверку конфликтующих, будут заведомо меньше 5, что и требовалось проверить.

Узел 10.

$\begin{matrix} 1 < x_{22} < 4, 0 < x_{23} < 3, x_{22} + x_{23} = 4 \Rightarrow x_{22} = 4 - x_{23}, τ_{11} = 3 (x_{22} + x_{23}) / 2 - 2 = 4; \\ τ_{12} = 4 - x_{22} / 2 < 3,5; τ_{13} = 8 - 5 x_{23} / 3 < 8; τ_{21} = 8 - x_{22} - x_{23} = 4; τ_{22} = 3 + x_{22} < 7; \\ τ_{23} = 2 + 5 x_{23} / 2 < 7; x_{11} = x_{22} + x_{23} - 2 = 2; x_{12} = 4 - x_{22} > 0; x_{13} = 3 - x_{23} > 0; \\ x_{21} = 4 - x_{22} - x_{23} = 0; x_{22} > 1; x_{23} > 0 \Rightarrow \\ m a x (4, 8 - 5 x_{23} / 2, 3 + x_{22} = 7 - x_{23}, 2 + 5 x_{23} / 2) \to i n f, \\ 0 < x_{23} < 3 \Rightarrow 2 + 5 x_{23} / 2 = 7 - x_{23} \Rightarrow x_{23} = 15 / 8 \Rightarrow i n f = 7 - x_{23} = 41 / 8 > 5 . \end{matrix}$

Нижняя оценка:

$m a x (3 (x_{22} + x_{23}) / 2 - 2, 4 - x_{22} / 2, 8 - 5 x_{23} / 3, 3 + x_{22}, 2 + 5 x_{23} / 3) \to m i n .$ (26)

И она равна 5. Это показывается так же, как в основном случае, когда все переменные положительны. Убеждаемся, как в основном варианте, что единственное решение $x_{23} = 1,8;$ $x_{22} = 2 .$ При этом общее значение уравненных частных показателей равно 5. Значит, остальные частные показатели, не вошедшие в четверку конфликтующих, будут заведомо меньше 5, что и требовалось проверить.

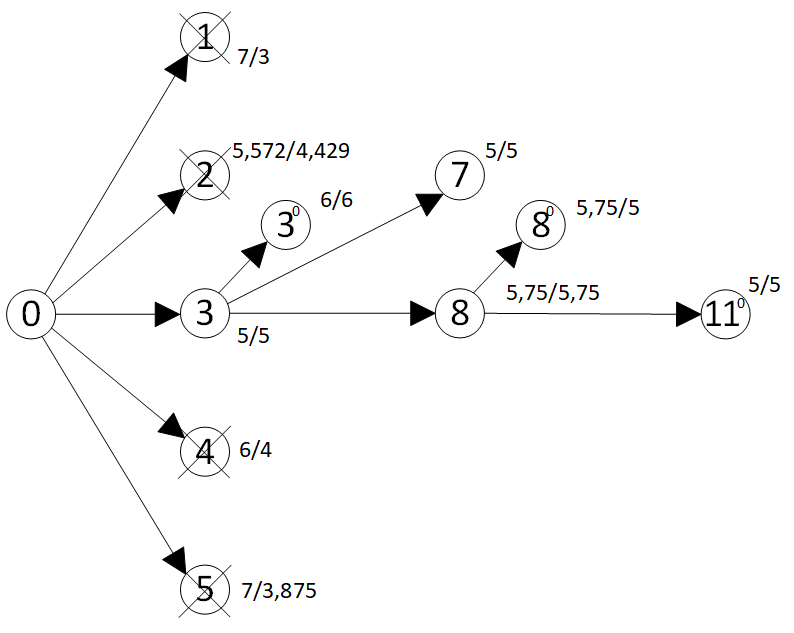
Процесс раскрытия вершин в примере 1 в классической схеме метода ветвей и границ с использованием правила отсева из (Финкильштейн, 1976) приведен на рис. 3. Через косую черту около узлов указана нижняя оценка, перед чертой стоит значение общего показателя в точке, в которой достигается нижняя оценка. Классическое правило отсева состоит в том, что на каждом шаге отбрасываются узлы со значениями не меньше текущего рекорда $r$ .

Рис. 3. Классическая схема метода ветвей и границ: рекорд — r=5 , точность — ε=0 , граница отсева — b=r=5

Замечание 5. Сокращение МВГ было вызвано тем, что к этому времени на этапе определения решения уже отброшены все пустые грани прямым методом перебора граней, что эквивалентно этому решению, но служит для наглядности описания МВГ. Это позволяет проиллюстрировать МВГ в полноформатном модельном примере 2×3 и, в частности, получить контрпример супер- (суб-) модулярности ТЗНД по времени (Хачатуров и др., 20212).

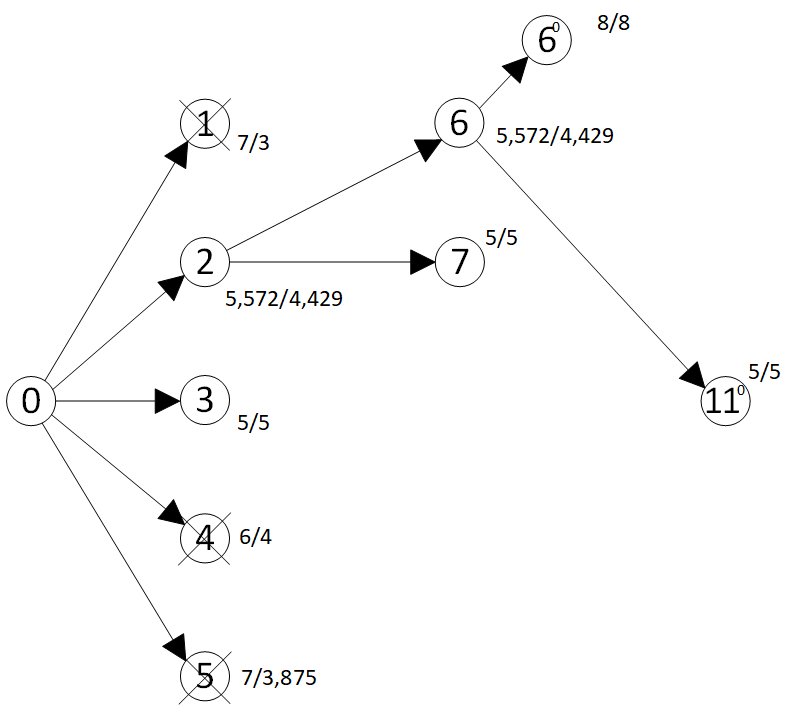
Процесс раскрытия вершин в примере 1 в ε-оптимальной схеме метода ветвей и границ с использованием правила отсева из (Финкильштейн, 1976) приведен на рис. 4. Обобщенное правило отсева состоит в том, что на каждом шаге отбрасываются узлы со значениями не меньше текущего рекорда $r$ , умноженного на $1 + ε$ .

Рис. 4. Классическая схема метода ветвей и границ: рекорд — $r = 5$ , точность — $ε = 0,15 = 15 %,$ граница отсечения — $b = (1 + ε) r = 5,75$

5. КОНТРПРИМЕР СУБМОДУЛЯРНОСТИ

Напомним, что функция $C = C (ω)$ , определенная на $2^{J},$ называется супер- (суб-) модулярной, если $\forall δ, ν \in 2^{J}$ выполняется неравенство $C (δ) + C (γ) \leq (\geq) C (δ \cup γ) + C (δ \cap γ) .$

Пример 2. Для краткости будем обозначать тип $θ (x)$ узла в примере 1 $x = (x_{11}, . . ., x_{23})$ по знакам соответствующих компонент, определяемых функцией $θ (x) = (s i g n x_{11}, . . ., s i g n x_{23})$ . Тогда $θ (x)$ можно отождествить с индикаторной функцией подмножества пар индексов, $B (x) = \{(i, j) : x_{i j} > 0\}$ и применять к ним теоретико-множественные операции объединения и пересечения.

1. Пусть $δ = 1,$ $θ (δ) = (1,1, 1,1, 1,0),$ $γ = 2,$ $θ (γ) = (0,1, 1,1, 1,1)$ . Тогда $θ (δ) \cup θ (γ) = (1,1, 1,1, 1,1) = θ (6),$ $θ (δ) \cap θ (γ) = (0,1, 1,1, 1,0) = θ (2)$ и $C (δ) + C (γ) = 8 + 6 \geq C (δ \cup γ) + C (δ \cap γ) = 5 + 2$ , где $C (γ) = I (B (γ))$ и $x$ отождествляется с номером $γ$ вершины поискового орграфа МВГ.

2. Пусть $δ = 3,$ $θ (δ) = (1,1, 1,1, 0,1),$ $γ = 5,$ $θ (γ) = (0,1, 1,1, 1,1)$ . Тогда $θ (δ) \cup θ (γ) = (1,1, 1,1, 1,1) = θ (6),$ $θ (δ) \cap θ (γ) = (0,1, 1,1, 0,1) = θ (3)$ и $C (δ) + C (γ) = 5,$ $750 + 5,125 \leq C (δ \cup γ) + C (δ \cap γ) = 5 + 6$ .

6. МЕТОД СУБГРАДИЕНТНОГО СПУСКА ДЛЯ НАХОЖДЕНИЯ НИЖНИХ ОЦЕНОК

Рассмотрим задачу нахождения нижней оценки в узле $\bar{B}$ :

${\underline{I}}_{B} = \underset{x \in X}{m i n} I_{B} (x) = \underset{x \in X}{m i n} \underset{(i, j) \in B}{m a x} τ_{i j} (x_{i j}) .$ (27)

Показатель (27) представляет собой выпуклую функцию. Исключая зависимые переменные из балансовых ограничений, как мы это делали в примере 1, приходим к задаче выпуклого программирования на множестве допустимых значений, заданной системой неравенств:

$F_{k} (x) \leq 0, k = 1, . . ., l$ (28)

с линейными функциями $F_{k} (x)$ и условием принадлежности объемлющему параллелепипеду $W$ :

$x_{i j} \in W_{i j} = [0, a_{i j}] \forall (i, j),$ (29)

которую можно свернуть в одно скалярное неравенство при помощи функции максимума

$\underset{k = 1, . . ., l}{m a x} F_{k} (x) \leq 0 .$ (30)

Эту задачу можно решить методом Б.Т. Поляка (Поляк, 1983):

$\begin{matrix} x_{i j}^{k + 1} = P_{W_{i j}} (x_{i j}^{k} - λ_{k} ν_{i j}^{k}) \forall (i, j), k = 0,1, . . ., \\ ν^{k} \in \{\begin{array}{l} \partial I_{B} (x^{k}), F (x^{k}) \leq 0, \\ \partial F (x^{k}), F (x^{k}) > 0, \end{array} λ_{k} \to + 0, \sum_{k = 0}^{\infty} λ_{k} = \infty, \end{matrix}$ (31)

где $k$ — номер шага; $λ_{k}$ — программный шаг метода; $P_{W_{i j}} (x_{i j})$ — оператор проектирования на компоненту $W_{i j}$ объемлющего параллелепипеда $W$ . Очевидно, что множество допустимых решений $X$ ограничено и имеет внутренние точки. Тогда согласно результатам (Поляк, 1983, с. 259) справедлива следующая теорема сходимости.

Теорема 2. Последовательность $[x^{k}]$ в методе (31) сходится к множеству решений задачи минимизации (27).

Замечание 6. Для получения значения основного показателя в узле, заданном подмножеством $B$ , решается задача минимизации штрафной функции $J_{B} (x)$ вместо $I_{B} (x)$ в (27) на всем множестве $X$ .

7. ПРИЛОЖЕНИЕ К ТЗНД ПО ЦЕНЕ

Пусть, как в обычной транспортной задаче, через $i = 1, . . ., m$ обозначены пункты производства (разработчики ПО) некоторого однородного товара (человеко-дней при стандартном 8-часовом дне чистого рабочего времени, определяемого по таймеру), через $j = 1, . . ., n$ — пункты его потребления (заказчики ПО). Даны величины: $a_{i} > 0$ — объем производства в пункте производства $i$ , $b_{j} > 0$ — объем потребления в пункте потребления j, отнесенные к одному дню (горизонту планирования).

Ищутся величины $x_{i j} \geq 0$ (объем перевозок из пункта $i$ в пункт j), удовлетворяющие обычным транспортным ограничениям (1) и минимизирующие функцию

$\underset{(i, j) : x_{i j} > 0}{m a x} c_{i j} (x_{i j})$ ,(32)

Где

$c_{i j} (x_{i j}) = \{\begin{array}{l} 0, x_{i j} = 0 \\ m a x (d_{i j} - c_{i j} x_{i j}, 0), x_{i j} > 0 . \end{array}$ (33)

Здесь $d_{i j}$ — базовые розничные цены одного дня производителя с учетом прибыли цифровой платформы, например 30%; $c_{i j} x_{i j}$ — скидка к цене на оптовую поставку объема $x_{i j}$ .

Введением дополнительных целочисленных переменных ТЗНД (1), (32), (33) по времени может быть сведена к классической ТЗ по времени. Способ такого сведения был указан в (Balinski, 1961) для ТЗФД, он проходит и для ТЗНД (1), (32), (33) по времени с некоторыми особенностями.

Рассмотрим частично-целочисленную задачу

$\underset{(i, j)}{m i n} m a x (d_{i j} y_{i j} - c_{i j} x_{i j}, 0) \to m a x$ (34)

при условиях (1) и дополнительных условиях (5).

Тогда задача (1), (5), (34) эквивалентна исходной задаче (1), (32), (33) и может быть аппроксимирована снизу (по значению) классической ТЗ по времени:

$\underset{(i, j)}{m i n} m a x (d_{i j} y_{i j} - c_{i j} x_{i j}, 0) \geq \underset{(i, j)}{m i n} m a x (d_{i j} - c_{i j} M_{i j}) y_{i j}, 0) = \underset{(i, j); x_{i j} > 0}{m i n} m a x (d_{i j} - c_{i j} M_{i j}, 0) \to m a x$ (35)

при условиях (1). Таким образом, задача (1), (32), (33) аппроксимирована снизу обычной ТЗ (1), (5), (35) по времени, которую можно решить венгерским методом расстановки пометок.

ЗАКЛЮЧЕНИЕ

В работе предложена практически значимая методика определения загрузки работ по исполнителям на рынке РПО, обеспечивающая учет скидок на опт. Основным результатом работы является постановка ТЗНД по времени, доказательство полунепрерывности общего показателя, из которого следует, что достигается его инфинум на ограниченном замкнутом множестве допустимых решений. Предложена геометрическая интерпретация решения задачи как минимума значений на непустых гранях и метод штрафов для их нахождения. Показано, что аналогично строятся нижние оценки показателя в методе ветвей и границ по непустым граням. Получена аппроксимация исходной задачей обобщенной задачей о назначения на узкие места методом (Balinski, 1961), которую можно решить модифицированным методом расстановки пометок, описанным в работе (Сергиенко, Симоненко, Симоненко, 2016), имеющим сложность $O (N l g N)$ , где $N = m + n$ . Приведены числовые примеры всех задач и алгоритмов их решения.

Практическая значимость работы определяется применением в трансакционных платформах на рынке РПО для загрузки заданий по терминологии, обоснованной в работе (Устюжанина, Дементьев, Евсюков, 2021). Построена статическая модель загрузки заданий с двумя группами агентов — компаниями–разработчиками ПО и компаниями–заказчиками ПО, которые могут опередить свои резервные цены на рынке повременной аренды разработанного ПО в двухсекторной модели экономики (Васин, Морозов, 2005). Дискриминируемыми агентами являются компании–заказчики ПО, которые оплачивают услуги оператора платформы в виде процентных надбавок, включенных оператором в цену работы компаний–разработчиков По. Имеются в виду платформы-рынки, взаимодействие экономических агентов на которых носит эпизодический характер разовых сделок. Предполагается удаленное взаимодействие, т.е. возможность коммуникации между агентами, находящимися на любом расстоянии друг от друга.

Допускается возможность масштабирования, что означает теоретическое отсутствие ограничений для расширения поля взаимодействия (числа пользователей). Такое расширение возможно за счет перекрестного сетевого эффекта, когда численность одного вида пользователей влияет на численность другого вида (спрос порождает предложение, и наоборот). Предполагается, что цифровые трансакционные платформы могут оказывать влияние на объем коммуникации через уровень и структуру цен. Исходя из базовых характеристик поля взаимодействия, платформа РПО относится к двусторонним рынкам. Для одноранговых (peer-to-peer) (Устюжанина, Дементьев, Евсюков, 2021) цифровых трансакционных платформ, к которым относятся платформы на рынке РПО, организующих торговые трансакции, непосредственными агентами являются поставщики — агенты, разрабатывающие ПО, и потребители — агенты, использующие разработанное ПО для повременной сдачи в аренду.

Операторы платформы на рынке РПО могут получать доход в виде платы пользователей за покупку, которые, в свою очередь, имеют доход в виде платы за временное пользование разработанных ПО в двухсекторной модели экономики (Васин, Морозов, 2005), цена которого определяет резервные цены потребителей.

В заключение следует отметить, что настоящая статья является продолжением серии статей (Перевозчиков, Лесик, 2014, 2016, 2020, 2021) в части замены базовой статической ТЗНД по стоимости ТЗНД по времени, которая может служить фундаментальной основой для построения соответствующих цифровых платформ.

GOST	Lesik I., Perevozchikov A. Market’s static model for software development based on a transport problem with non-fixed time additions // Economics and the Mathematical Methods. – 2022. – V. 58. – Issue 2 C. 97-111 . URL: https://emmras.ru/s042473880019969-4-1/?version_id=92899. DOI: 10.31857/S042473880019969-4
MLA	Lesik, Ilya, Perevozchikov, Aleksandr "Market’s static model for software development based on a transport problem with non-fixed time additions." Economics and the Mathematical Methods. 58.2 (2022).:97-111. DOI: 10.31857/S042473880019969-4
APA	Lesik I., Perevozchikov A. (2022). Market’s static model for software development based on a transport problem with non-fixed time additions. Economics and the Mathematical Methods. vol. 58, no. 2, pp.97-111 DOI: 10.31857/S042473880019969-4

Market’s static model for software development based on a transport problem with non-fixed time additions

You can

ВВЕДЕНИЕ

1. ПОСТАНОВКА ТРАНСПОРТНОЙ ЗАДАЧИ С НЕФИКСИРОВАННЫМИ ДОБАВКАМИ ПО ВРЕМЕНИ

2. АППРОКСИМАЦИЯ ЗАДАЧИ

3. МЕТОД ВЕТВЕЙ И ГРАНИЦ

4. ПРИМЕР ТОЧНОГО РЕШЕНИЯ ЗАДАЧИ

5. КОНТРПРИМЕР СУБМОДУЛЯРНОСТИ

6. МЕТОД СУБГРАДИЕНТНОГО СПУСКА ДЛЯ НАХОЖДЕНИЯ НИЖНИХ ОЦЕНОК

7. ПРИЛОЖЕНИЕ К ТЗНД ПО ЦЕНЕ

ЗАКЛЮЧЕНИЕ

References

Market’s static model for software development based on a transport problem with non-fixed time additions

You can

ВВЕДЕНИЕ

1. ПОСТАНОВКА ТРАНСПОРТНОЙ ЗАДАЧИ С НЕФИКСИРОВАННЫМИ ДОБАВКАМИ ПО ВРЕМЕНИ

2. АППРОКСИМАЦИЯ ЗАДАЧИ

3. МЕТОД ВЕТВЕЙ И ГРАНИЦ

4. ПРИМЕР ТОЧНОГО РЕШЕНИЯ ЗАДАЧИ

5. КОНТРПРИМЕР СУБМОДУЛЯРНОСТИ

6. МЕТОД СУБГРАДИЕНТНОГО СПУСКА ДЛЯ НАХОЖДЕНИЯ НИЖНИХ ОЦЕНОК

7. ПРИЛОЖЕНИЕ К ТЗНД ПО ЦЕНЕ

ЗАКЛЮЧЕНИЕ

References

Via social network