Народнохозяйственная производственная функция России в 1990—2017 гг.

Пономарева Ольга С.; Афанасьев Антон А.

doi:10.31857/S042473880006708-7

Код статьи

S042473880006708-7-1

DOI

10.31857/S042473880006708-7

Тип публикации

Статья

Статус публикации

Опубликовано

Авторы

Пономарева Ольга Станиславна

Должность: Senior Research Scholar
Аффилиация: Central Economics and Mathematics Institute, Russian Academy of Sciences
Адрес: Moscow, Russian Federation

Афанасьев Антон Александрович

Должность: Ведущий научный сотрудник
Аффилиация: Центральный экономико-математический институт РАН
Адрес: Нахимовский проспект, дом 47

Том/ Выпуск

Том 56 / Номер 1

Страницы

67-78

Аннотация

В статье (Афанасьев, Пономарева, 2014), опубликованной в этом журнале, авторы провели эконометрическое исследование трех видов макроэкономических производственных функций Российской Федерации во временном интервале 1990—2012 гг.: функции с трудом и капиталом; функции с учетом производственной инфраструктуры, представляющей собой основные фонды отраслей транспорта и связи России; и функции с мировой ценой на нефть марки «Брент». В данной работе, являющейся продолжением вышеуказанной, эконометрическое исследование производственных функций проводится на расширенном временном интервале — 1990–2017 гг. — и с учетом корректировок статистических данных о мировой цене на нефть в 2011–2012 гг. Исследованные производственные функции адекватно — с точки зрения классических критериев эконометрики и содержательного смысла — описывают процесс расширенного воспроизводства народного хозяйства Российской Федерации в 1990–2017 гг. Отличительной особенностью настоящего исследования, как и работы (Афанасьев, Пономарева, 2014), является методика перечета основных фондов в сопоставимые цены, относительно стабильные во времени коэффициенты исследованных производственных функций при расширении временного ряда, хорошая прогнозная сила производственных функций, характеризующаяся невысокими ошибками ex-postпрогноза.

Ключевые слова

народное хозяйство, производственная функция, Россия, капитал, труд, цена, нефть марки «Брент».

Дата публикации

20.03.2020

Год выхода

2020

Всего подписок

Всего просмотров

2101

Экономико-математическому анализу производственных функций на народнохозяйственном и отраслевом уровнях посвящено большое число работ как российских, так и зарубежных авторов (Cobb, Douglas, 1928; Solow, 1957; Канторович, Вайнштейн, 1967; Канторович, Жиянов, 1973; Михалевский, Соловьев, 1966; Гребенников, 1968, 1969; Яременко, Ершов, Смышляев, 1974; Варшавский, 1976; Иванилов, 1983; Клейнер, 1986; Суворов Н., Суворов А., 1988; Макаров, 1999; Бессонов, 2002; Гладышевский, 2004; Бродский, 2006; Шамис, 2009; Афанасьев, 2007, 2008, 2009а, 2009б, 2014; Ершов, 2013 Афанасьев, Пономарева, 2014, 2016; Баранов, Бессонов, 2018). Настоящая работа является продолжением нашего эконометрического исследования производственной функции российской экономики, результаты которого за 1990–2012 гг. опубликованы в статье (Афанасьев, Пономарева, 2014). В данной работе производственная функция исследуется на расширенном временном интервале 1990–2017 гг.

Мы рассматриваем два вида производственных функций экономики России:

а) без мировой цены на нефть марки «Брент»

$Y_{t (1990)} / L_{t} = e^{α_{0}} {(z_{t} {\bar{Ф}}_{t (1990)} / L_{t})}^{α_{1}};$ (1)

б) с мировой ценой на нефть марки «Брент»

$Y_{t (1990)} / L_{t} = e^{α_{0}} {(z_{t} {\bar{Ф}}_{t (1990)} / L_{t})}^{α_{1}} e^{γ p_{t (2010)}}$ ,(2)

где $Y_{t (1990)}$ — валовой внутренний продукт России в сопоставимых ценах 1990 г. в году $t$ ; ${\bar{Ф}}_{t (1990)}$ — среднегодовая стоимость основных фондов народного хозяйства в сопоставимых ценах 1990 г. в году $t$ ; $z_{t}$ — степень загрузки производственных мощностей в российской промышленности в году $t$ ; $L_{t}$ — среднегодовая численность занятого в народном хозяйстве населения в году $t$ ; $p_{t (2010)}$ — мировая цена на нефть марки «Брент» в сопоставимых ценах 2010 г.

Как и в работе (Афанасьев, Пономарева, 2014), для эконометрического исследования производственных функций авторами были использованы статистические данные Росстата (ВВП, основные фонды, труд, среднегодовые индексы фактических цен производителей в капитальном строительстве), Российского экономического барометра (РЭБ) (степень загрузки производственных мощностей) и Мирового банка (WBCPD) (мировая цена нефти марки «Брент») (табл. 1). Расчет среднегодовой стоимости основных фондов в сопоставимых ценах 1990 г. за 1991–2017 гг. приведен в табл. 2, он осуществлялся на основе статистических данных Росстата по методике, изложенной в работе (Афанасьев, Пономарева, 2014). С 1991 г. среднегодовая стоимость в сопоставимых ценах 1990 г. вычислялась как среднее арифметическое между стоимостью основных фондов на начало отчетного года в сопоставимых ценах $Ф Н_{t (1990)}$ и стоимостью основных фондов на конец отчетного года в сопоставимых ценах $Ф К_{t (1990)}$ :

${\bar{Ф}}_{t (1990)} = 0,5 (Ф Н_{t (1990)} + Ф К_{t (1990)}),$ (3)

$Ф К_{t (1990)} = Ф Н_{t (1990)} + Ф В_{t (1990)} - Ф Л_{t (1990)},$ (4)

$Ф Н_{t (1990)} = Ф К_{t - 1 (1990)}$ , $Ф Н_{1991 (1990)} = Ф Н_{1991},$ (5)

$Ф В_{t (1990)} = Ф В_{t} / \prod_{i = 1991}^{t} И К С_{i},$ (6)

$Ф Л_{t (1990)} = Ф Л_{t} / \prod_{i = 1992}^{t} И Л_{i},$ (7)

$И Л_{t} = Ф Н_{t} / Ф К_{t - 1},$ (8)

где $t$ — индекс года; $Ф В_{t (1990)}$ — стоимость введенных в действие новых основных фондов в сопоставимых ценах 1990 г.; $Ф Л_{t (1990)}$ — стоимость ликвидированных основных фондов в сопоставимых ценах 1990 г.; $Ф Н_{t}$ и $Ф К_{t}$ — стоимости основных фондов в фактических ценах на начало и конец года соответственно; $Ф В_{t}$ и $Ф Л_{t}$ — стоимости введенных в действие новых и ликвидированных основных фондов в фактических ценах соответственно; $И К С_{t}$ — среднегодовой индекс фактических цен производителей в капитальном строительстве (январь–декабрь отчетного года к январю–декабрю предыдущего года); $И Л_{t}$ — индекс фактической переоценки основных фондов.

Таблица 1. Статистические данные для эконометрического исследования за 1990–2017 гг.

$t$	$Y_{t (1990)}$ , млрд руб.	${\bar{Ф}}_{t (1990)}$ , млн руб.	$z_{t}$ , %	$L_{t}$ ^*, тыс. человек	$p_{t (2010)}$ ^**, долл./бар.
1990	644	1 871 649	100	75 325	28,65
1991	612	1 957 288	100	73 848	24,50
1992	523	2 009 054	73	72 071	23,14
1993	478	2 030 396	74	70 852	19,72
1994	417	2 014 984	61	68 484	18,91
1995	400	1 995 229	60	66 441	18,57
1996	386	1 983 823	54	65 950	22,90
1997	391	1 967 098	54	64 639	22,22
1998	371	1 953 216	55	63 642	15,48
1999	394	1 953 747	62	63 963	22,10
2000	434	1 962 932	66	64 517	35,54
2001	456	1 976 006	69	64 980	31,89
2002	477	1 993 845	70	65 574	32,99
2003	512	2 015 564	73	65 979	36,24
2004	549	2 040 209	74	66 407	45,05
2005	584	2 074 736	76	66 792	62,07
2006	632	2 119 496	78	67 174	72,72
2007	686	2 169 707	80	68 019	76,18
2008	722	2 229 842	77	68 474	94,95
2009	665	2 292 706	65	67 463	64,13
2010	695	2 350 079	72	67 577	79,64
2011	725	2 416 816	78	67 727	99,97
2012	750	2 499 424	79	67 968	101,61
2013	760	2 581 327	78	67 901	99,21
2014	765	2 644 159	77	67 813	91,59
2015	744	2 673 133	75	68 389	53,65
2016	742	2 696 319	77	68 430	46,98
2017	753	2 729 568	79	68 127	55,91

Источники: статистические данные за 1990–2012 см. (Афанасьев, Пономарева, 2014); табл. 2; РЭБ, 2018, с. 44; Российский статистический ежегодник, 2016, с. 109, 267, 2017, с. 258, 2018, с. 259; Россия в цифрах, 2017, с. 93; WBCPD, 2017, 2019.

^* В связи с изменением методики расчета Росстатом среднегодовой численности занятых в народном хозяйстве показатель за 2017 г. вычислен авторами по среднегодовому темпу роста за 2017 г. (РЦ 2018, с. 91; РСЕ 2017, с. 49).

^** Уточненные данные за 2011–2012 гг.

Таблица 2. Расчет среднегодовой стоимости основных фондов народного хозяйства России в сопоставимых ценах 1990 г. за 1991–2017 гг.¹

Год	В фактических ценах, млн руб. (до 1994 г. — неденоминированных)	$И К С_{t},$ раз к предыдущему году	$И Л_{t},$ раз к предыдущему году	В сопоставимых ценах 1990 г., млн неденоминированных руб.
	Наличие на начало отчетного года	Введено в действие новых	Ликвидировано (списано)	Наличие на конец отчетного года			Наличие на начало отчетного года	Введено в действие новых	Ликвидировано (списано)	Наличие на конец отчетного года	Среднегодовая стоимость
1990	1 833 568	135 925	41 191	1 926 916	1,000	–	–	–	–	–	1 871 649
1991	1 926 916	175 540	41 719	2 061 141	1,713	1,000	1 926 916	102 463	41 719	1 987 660	1 957 288
1992	41 808 023	2 005 179	606 689	43 214 607	16,100	20,284	1 987 660	72 697	29 910	2 030 447	2 009 054
1993	43 214 607	15 093 139	958 938	63 860 780	11,600	1,000	2 030 447	47 172	47 276	2 030 344	2 030 396
1994	1 189 560 972	72 349 654	27 727 669	1 221 494 279	5,300	18,627	2 030 344	42 665	73 385	1 999 623	2 014 984
1995	5 182 039 730	230 406 948	93 864 056	5 306 460 330	2,730	4,242	1 999 623	49 770	58 558	1 990 835	1 995 229
1996	13 072 378 021	334 301 914	221 157 712	13 250 160 200	1,720	2,463	1 990 835	41 984	56 007	1 976 812	1 983 823
1997	13 286 271 536	406 471 841	253 452 937	13 411 950 567	1,145	1,003	1 976 812	44 583	64 011	1 957 384	1 967 098
1998	14 125 670	428 564	220 572	14 277 540	1,055	1,053	1 957 384	44 555	52 892	1 949 047	1 953 216
1999	14 206 427	597 306	157 999	14 327 234	1,308	0,995	1 949 047	47 476	38 077	1 958 446	1 953 747
2000	16 479 505	841 245	181 607	17 335 233	1,422	1,150	1 958 446	47 022	38 050	1 967 418	1 962 932
2001	20 162 861	1 115 886	184 789	21 414 799	1,236	1,163	1 967 418	50 463	33 287	1 984 594	1 976 006
2002	24 430 544	1 615 063	290 000	26 333 273	1,136	1,141	1 984 594	64 294	45 791	2 003 096	1 993 845
2003	30 329 106	1 815 658	295 665	32 173 286	1,104	1,152	2 003 096	65 470	40 535	2 028 032	2 015 564
2004	32 541 444	1 972 112	287 079	34 873 724	1,124	1,011	2 028 032	63 267	38 912	2 052 386	2 040 209
2005	38 366 273	2 943 686	309 183	41 493 568	1,141	1,100	2 052 386	82 794	38 093	2 097 087	2 074 736
2006	43 822 840	3 252 436	320 797	47 489 498	1,112	1,056	2 097 087	82 242	37 424	2 141 906	2 119 496
2007	54 251 541	4 296 411	379 410	60 391 454	1,152	1,142	2 141 906	94 347	38 744	2 197 508	2 169 707
2008	64 533 994	5 744 850	429 373	74 441 095	1,194	1,069	2 197 508	105 700	41 032	2 262 176	2 229 842
2009	76 218 866	6 356 223	537 331	82 302 969	1,052	1,024	2 262 176	111 212	50 151	2 323 236	2 292 706
2010	85 664 471	6 275 935	563 203	93 185 612	1,054	1,041	2 323 236	104 188	50 503	2 376 921	2 350 079
2011	94 876 442	8 813 314	614 888	108 001 247	1,092	1,018	2 376 921	133 944	54 155	2 456 711	2 416 816
2012 2013 2014 2015 2016 2017	108 819 425 120 246 829 133 352 499 149 327 112 164 494 574 183 087 077	10 338 476 11 160 485 10 887 946 10 721 081 13 256 290 12 484 066	702 185 810 193 1 044 973 1 304 140 1 274 050 1 176 041	121 268 908 133 521 531 147 429 656 160 725 261 183 403 693 194 649 464	1,070 1,058 1,048 1,105 1,066 1,036	1,008 0,992 0,999 1,013 1,023 0,998	2 456 711 2 542 136 2 620 518 2 667 800 2 678 467 2 714 172	146 804 149 803 139 518 124 314 144 188 131 101	61 379 71 422 92 235 113 648 108 482 100 310	2 542 136 2 620 518 2 667 800 2 678 467 2 714 172 2 744 963	2 499 424 2 581 327 2 644 159 2 673 133 2 696 319 2 729 568

Источники: ГМЦ Росстата, Росстат, расчеты авторов по формулам (3)–(8), данные Росстат за 1990 г.

Результаты эконометрического исследования производственных функций российской экономики без мировой цены на нефть марки «Брент» (1) и с мировой ценой на нефть марки «Брент» (2), выполненного на основе статистических данных из табл. 1, представлены в табл. 3 и 4.

Таблица 3. Результаты эконометрического исследования производственной функции российской экономики без мировой цены на нефть марки «Брент» (1) за 1990–2004 гг.

Годы	$α_{0}$	$α_{1}$	$R^{2}$	$D W$
1990–1993	–7,28 (–7)	0,77 (2,47)	0,75	2,42
1990–1994	–7,52 (–13)	0,85 (5)	0,88	2,93
1990–1995	–7,64 (–18)	0,88 (6)	0,90	3,10
1990–1996	–7,48 (–23)	0,83 (8)	0,92	2,69
1990–1997	–7,35 (–25)	0,79 (8)	0,92	2,11
1990–1998	–7,39 (–29)	0,80 (9)	0,92	2,38
1990–1999	–7,41 (–28)	0,81 (9)	0,91	2,10
1990–2000	–7,41 (–30)	0,81 (10)	0,91	2,18
1990–2001	–7,41 (–32)	0,81 (10)	0,91	2,19
1990–2002	–7,43 (–33)	0,81 (11)	0,91	2,19
1990–2003	–7,48 (–33)	0,83 (11)	0,91	2,09
1990–2004	–7,59 (–31)	0,87 (11)	0,90	1,74

Примечание. В скобках приведены t-статистики.

Источник: Афанасьев, Пономарева, 2014.

Таблица 4. Результаты эконометрического исследования производственной функции российской экономики с мировой ценой на нефть марки «Брент» (2) для 1990–2017 гг.

Годы	$e^{α_{0}}$	$α_{1}$	$γ$	$R^{2}$	$D W$
1990–2000	0,00064 (–29)	0,76 (8)	0,003 (1,02)
1990–2001	0,00064 (30)	0,77 (9)	0,002 (0,95)	0,92	1,85
1990–2002	0,00064 (–32)	0,77 (9)	0,002 (1,15)	0,92	1,87
1990–2003	0,00064 (–33)	0,77 (9)	0,003 (1,59)	0,93	1,79
1990–2004	0,00064 (–33)	0,76 (10)	0,004 (2,63)	0,93	1,60
1990–2005	0,00064 (35)	0,76 (10)	0,004 (4)	0,95	1,69
1990–2006	0,00064 (–36)	0,76 (11)	0,004 (5)	0,96	1,69
1990–2007	0,00064 (–37)	0,76 (11)	0,004 (6)	0,97	1,67
1990–2008	0,00064 (39)	0,76 (11)	0,004 (8)	0,97	1,66
1990–2009	0,00071 (–27)	0,72 (8)	0,004 (7)	0,95	1,41
1990–2010	0,00071 (–28)	0,72 (8)	0,004 (8)	0,96	1,78
1990–2011^*	0,00076 (–26)	0,71 (7)	0,004 (7)	0,95	1,56
1990–2012^*	0,00080 (–25)	0,70 (7)	0,004 (6)	0,95	1,27
1990–2013	0,00082 (–24)	0,69 (7)	0,004 (6)	0,95	1,14
1990–2014	0,00082 (–25)	0,68 (7)	0,004 (6)	0,96	1,12
1990–2015	0,00066 (–28)	0,75 (8)	0,003 (6)	0,95	1,23
1990–2016	0,00058 (–32)	0,80 (10)	0,003 (6)	0,95	1,23
1990–2017	0,00057 (–35)	0,81 (11)	0,003 (6)	0,96	1,26

Примечание. В скобках приведены t-статистики; «*» отмечены данные с учетом корректировки Мировым банком мировой цены на нефть марки «Брент» в 2011–2012 гг.

Таблица 5. Ошибка ex-post прогноза АРЕ на 2001–2017 гг. по функции (2), %

Год ex-post прогноза	Обучающая выборка за период с 1990 г. По:
	2000 г.	2001 г.	2002 г.	2003 г.	2004 г.	2005 г.	2006 г.	2007 г.	2008 г.	2009 г.	2010 г.	2011 г.	2012 г.	2013 г.	2014 г.	2015 г.	2016 г.
2001	2,4
2002	0,2	0,5
2003	1,8	2,7	2,5
2004	4,1	5,4	5,2	4,1
2005	2,1	4,3	3,9	2,0	1,2
2006	3,2	6,0	5,5	3,1	1,0	0,1
2007	6,3	9,1	8,6	6,1	1,9	2,8	2,9
2008	6,7	10,5	9,8	6,5	0,7	2,0	2,1	0,6
2009	17,0	19,0	18,6	16,9	14,0	14,6	14,7	13,9	13,8
2010	8,5	11,5	10,9	8,4	3,9	4,9	5,0	3,9	3,7	1,4
2011	0,9	3,4	2,6	1,2	7,9	6,4	6,3	8,0	8,3	11,6	12,0
2012	1,6	2,8	2,0	1,9	8,8	7,2	7,1	8,9	9,1	12,4	12,8	9,5
2013	1,1	3,2	2,4	1,4	7,9	6,5	6,4	8,0	8,3	11,3	11,7	8,5	6,4
2014	0,9	4,7	4,0	0,6	5,1	3,8	3,7	5,1	5,4	7,8	8,2	5,3	3,4	2,4
2015	9,3	10,9	10,6	9,2	7,1	7,5	7,6	7,1	7,0	6,7	6,6	7,6	8,5	9,1	9,4
2016	8,4	9,6	9,4	8,3	6,6	7,0	7,0	6,7	6,7	6,8	6,7	7,5	8,3	8,9	9,2	6,8
2017	4,8	6,5	6,2	4,6	2,2	2,8	2,8	2,2	2,2	2,0	1,9	3,1	4,2	4,9	5,3	2,8	1,1
Средняя	4,7	6,9	6,8	5,3	5,3	5,5	5,9	6,4	7,2	7,5	8,6	6,9	6,2	6,3	8,0	4,8	1,1

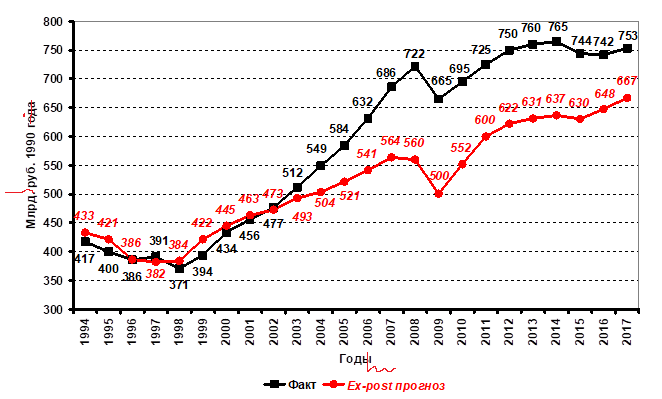
Как видно из данных, представленных в табл. 3 и 4, производственные функции (1) и (2) адекватно описывают процесс расширенного воспроизводства народного хозяйств нашей страны с точки зрения как содержательного смысла, так и канонических критериев эконометрики: функция (1) — во временных промежутках, начинающихся с 1990 г. и оканчивающихся 1993–2004 гг., а функция (2) — во временных промежутках начинающихся с 1990 г. и оканчивающихся 2000–2017 гг. Отметим, что функция (1) также достаточно точно прогнозирует объемы российского ВВП в сопоставимых ценах до 2004 г. (рис. 1–2). В самом деле, ретроспективная оценка абсолютной величины относительной ошибки прогноза $A P E$ (ошибка ex-post-прогноза) в 1993–2004 гг., вычисляемая по формуле

$A P E = |\frac{e x - p o s t п р о г н о з н ы й В В П}{ф а к т и ч е с к и й В В П} - 1| \times 100 %$ ,

не превышает 7%. Однако при расширении временного промежутка до 2014 г. качество эконометрических оценок и точность прогнозов снижается, что скорее всего вызвано усилением влияния мировой цены на нефть на экономическое развитие России с 2004 г. Вместе с тем интересен тот факт, что, несмотря на начавшееся в 2004 г. расхождение, направление динамики ex-post-прогноза реального ВВП России по функции (1), исследованной в 1990–1993 гг., практически везде (кроме 1997, 2008 и 2016 г.) соответствует направлению динамики фактического реального ВВП в 1994–2017 гг. (рис. 1, 2).

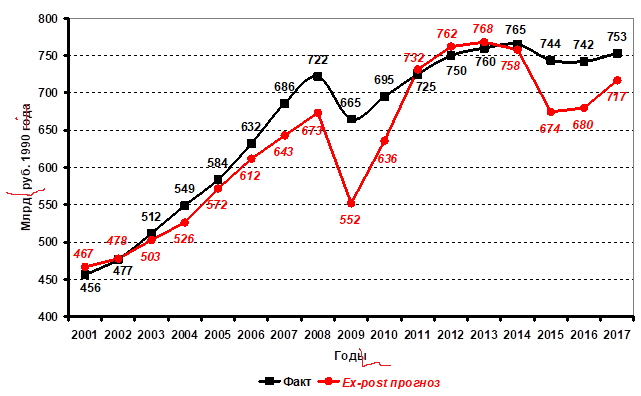
Функция (2) с мировой ценой на нефть дает лучшие результаты ex-post-прогнозов на 2005–2017 гг., чем функция (1) (табл. 5, рис. 3, 4). Наименьшими средними ошибками ex-post прогноза обладают функции, исследованные с 1990 г. по 2000, 2015 и 2016 г. Средние ошибки $A P E$ составляют соответственно 4,7, 4,8 и 1,1% (табл. 5).

Результаты эконометрического исследования функции (2), изложенные в табл. 4 и проиллюстрированные на рис. 5–7, свидетельствуют о нижеследующем.

1. Коэффициент нейтрального технического прогресса $e^{α_{0}}$ в течение 2000–2008 гг. почти не изменялся, находясь на уровне 0,00064. С 2009 по 2014 г. наблюдался его рост до 0,00082, а в 2015–2017 гг. — значительное падение до 0,00057, что ниже уровня 2000–2008 гг.

2. Эластичность ВВП по основным фондам в 2000–2008 гг. не претерпевала существенных изменений, находясь в пределах 0,76–0,77, но в 2009–2014 заметно снизилась до 0,68, а в 2015–2017 — существенно выросла до 0,81, превысив уровень 2000–2008 гг. Такая динамика говорит о вытеснении капитала трудом в 2009–2014 гг. и вытеснении труда капиталом в 2015–2017 гг., начавшемся в условиях внешнеэкономических и внешнеполитических ограничений, в которых российская экономика оказалась с 2014 г.

3. Коэффициент при мировой цене на нефть марки «Брент» в сопоставимых ценах 2010 г. оставался неизменным на уровне 0,004 с 2004 по 2014 г., т.е. в течение 11 лет, а в 2015–2017 гг. (в условиях санкционного давления на экономику России) немного снизился до 0,003, что может свидетельствовать о некотором небольшом ослаблении зависимости народного хозяйства нашей страны от мировых цен на энергоносители. Этот вывод косвенно подтверждается тем, что фактические и ex-post-прогнозные значения ВВП по функции без цены на нефть (1) начинают сближаться в 2015–2017 гг. (см. рис. 1 и 2).

4. Ошибки ex-post-прогноза на 2011–2014 гг. по функции (2), исследованной в 1990–2000 гг., не превышают 1,6%, ошибки прогноза на 2015 и 2016 г. являются более высокими и составляют 9,3 и 8,4% соответственно, а ошибка прогноза на 2017 г. равна 4,8%.

Рис. 1. Динамика фактического и ex-post прогнозного на 1994–2017 гг. (по функции (1), исследованной в 1990–1993 гг.) ВВП Российской Федерации в сопоставимых ценах 1990 г., млрд руб. 1990 г.

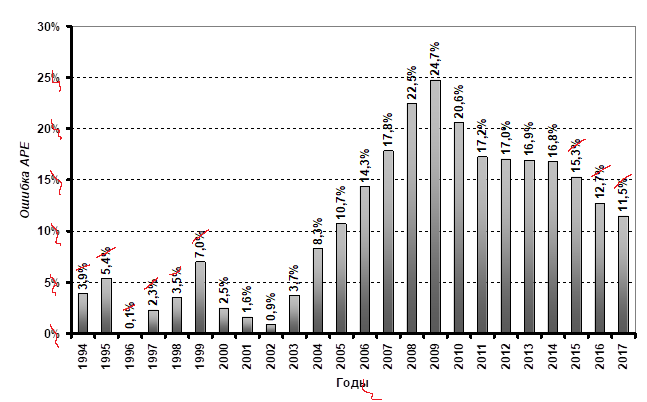
Рис. 2. Ошибки ex-post прогноза APE на 1994–2017 гг. (по функции (2), исследованной в 1990–1993 гг.) ВВП России в сопоставимых ценах 1990 г.

Рис. 3. Динамика фактического и ex-post прогнозного на 2001–2017 гг. (по функции (2), исследованной в 1990–2000 гг.) ВВП Российской Федерации в сопоставимых ценах 1990 г., млрд руб. 1990 г.

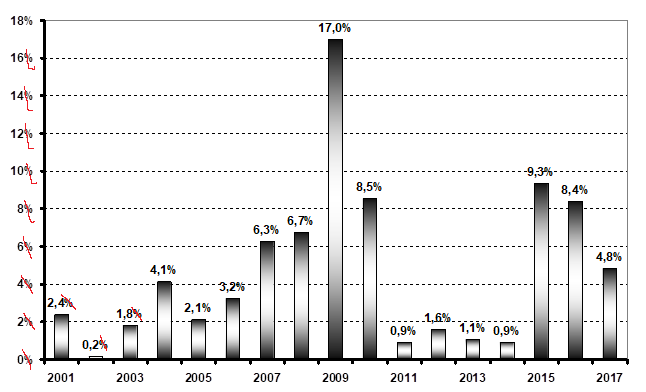
Рис. 4. Ошибки ex-post прогноза APE на 2001–2016 гг. (по функции (2), исследованной в 1990–2000 гг.) ВВП России в сопоставимых ценах 1990 г.

Рис. 5. Коэффициент нейтрального технического прогресса eα0 функции (2), исследованной во временных промежутках, начинающихся 1990 г. и оканчивающихся 2000–2017 гг.

Рис. 6. Эластичность ВВП России по основным фондам α1 функции (2), исследованной во временных промежутках, начинающихся 1990 г. и оканчивающихся 2000–2017 гг.

Рис. 7. Коэффициент при цене на нефть марки "Брент" $γ$ функции (2), исследованной во временных промежутках, начинающихся 1990 г. и оканчивающихся 2000–2017 гг.

В заключение отметим, что исследованные нами производственные функции могут быть использованы профильными министерствами и ведомствами России в качестве эффективного инструмента анализа и прогнозирования динамики социально-экономического развития нашей страны.

Библиография

1. Афанасьев А.А. (2007). Производственная функция нефтяной промышленности России в 1961–2005 гг. // Проблемы экономики и управления нефтегазовым комплексом. № 4. С. 18–29.
2. Афанасьев А.А. (2008). Экономико-математическое моделирование и прогнозирование добычи природного газа в Тюменской области // Газовая промышленность. № 6. С. 19–25.
3. Афанасьев А.А. (2009а). Производственная функция российской экономики с учетом основных фондов транспорта и связи в 1990–2007 гг. В сб.: “Системное моделирование социально-экономических процессов: Труды 32-й Международной школы-семинара, Вологда, 5–10 октября 2009 г.”. Гребенников В.Г., Щепина И.Н., Эйтингон В.Н. (ред.). Часть 1. Воронеж: Издательско-полиграфический центр ВГУ. С. 93–97.
4. Афанасьев А.А. (2009б). Производственные функции газодобывающей промышленности Тюменской области и дочерних обществ ОАО “Газпром” в 1993–2007 гг. // Экономика и математические методы. Т. 45. № 2. С. 37–53.
5. Афанасьев А.А. (2014). Устойчивость стратегических целей – необходимое условие развития Газпрома как глобальной энергетической компании // Газовая промышленность. № 704. С. 10–20.
6. Афанасьев А.А., Пономарева О.С. (2014). Производственная функция народного хозяйства России в 1990–2012 гг. // Экономика и математические методы. Т. 50. № 4. С. 21–33.
7. Афанасьев А.А., Пономарева О.С. (2016). Макроэкономическая производственная функция России в 1990–2016 гг. В сб.: Управление развитием крупномасштабных систем (MLSD’2018). Том 1. М.: ИПУ РАН. С. 408–414.
8. Баранов Э.Ф., Бессонов В.А. (2018). Взгляд на российскую экономическую трансформацию // Вопросы экономики. № 11. С. 142–158.
9. Бессонов В.А. (2002). Проблемы построения производственных функций в российской переходной экономике. В кн.: Бессонов В.А., Цухло С.В. “Анализ динамики российской переходной экономики”. М.: Институт экономики переходного периода. С. 5–89.
10. Бродский Б.Е. (2006). О влиянии реального обменного курса рубля на российскую экономику // Прикладная эконометрика. № 4. С. 90–104.
11. Варшавский Л.Е. (1976). Генетическое моделирование экономического развития нефте- и газодобывающей промышленности (на примере газодобывающей промышленности СССР). Дисс. на соиск. уч. степ. кандидата экономических наук по специальности 08.00.13. М.: ЦЭМИ АН СССР.
12. Гладышевский А.И. (2004). Прогнозирование воспроизводственных процессов в экономике (инвестиционный аспект). М.: Макс Пресс.
13. Гребенников В.Г. (1968). Некоторые проблемы взаимосвязи темпов роста национального дохода, фондоотдачи и норм накопления // Экономика и математические методы. Т. 4. Вып. 4. С. 583–596.
14. Гребенников В.Г. (1969). Использование производственных функций для анализа долгосрочных тенденций экономического роста США. В сб.: “Методы и модели долгосрочного анализа”. М.: ЦЭМИ АН СССР. С. 51–77.
15. Ершов Э.Б. (2013). Композитные производственные функции // Экономический журнал Высшей школы экономики. Т. 17. № 1. С. 108–129.
16. Иванилов Ю.П. (1983). Производственная народнохозяйственная функция. М.: ВЦ АН СССР.
17. Канторович Л.В., Вайнштейн А.Л. (1967). Об исчислении нормы эффективности на основе однопродуктовой модели развития хозяйства // Экономика и математические методы. Т. 3. Вып. 5. С. 697–710.
18. Канторович Л.В., Жиянов В.И. (1973). Однопродуктовая динамическая модель экономики, учитывающая изменение структуры фондов при наличии технического прогресса // Доклады АН СССР. Т. 211. № 6. С. 1280–1283.
19. Клейнер Г.Б. (1986). Производственные функции: теория, методы, применение. М: Финансы и статистика.
20. Макаров В.Л. (1999). Вычислимая модель российской экономики (RUSEC). Препринт № wp/99/069. М.: ЦЭМИ РАН.
21. Михалевский Б.Н., Соловьев Ю.П. (1966). Производственная функция народного хозяйства СССР в 1951–1963 гг. // Экономика и математические методы. Т. 2. Вып. 6. С. 10–21.
22. РСЕ (2016). Российский статистический ежегодник. 2016: Статистический сборник. М.: Росстат.
23. РСЕ (2017). Российский статистический ежегодник. 2017: Статистический сборник. М.: Росстат.
24. РСЕ (2018). Российский статистический ежегодник. 2018: Статистический сборник. М.: Росстат.
25. РЦ (2017). Россия в цифрах. 2017: Краткий статистический сборник. М.: Росстат.
26. РЭБ (2018) // Российский экономический барометр. № 3–4.
27. Суворов Н.В., Суворов А.В. (1988). Методологические вопросы измерения эффективности общественного производства // Экономика и математические методы. Т. 24. Вып. 3. С. 400–409.
28. Шамис Л.В. (2009). Проблемы рационального замещения производственных ресурсов (на примере газодобывающей отрасли) // Проблемы экономики и управления нефтегазовым комплексом. № 8. С. 13–18.
29. Яременко Ю.В., Ершов Э.Б., Смышляев А.С. (1974). Исследование взаимосвязи факторов роста экономики СССР в 1950–1970 гг. В кн.: “Математические методы решения экономических задач”. М.: Наука. С. 31–48.
30. Cobb Ch.W., Douglas P.H. (1928). A Theory of Production // The American Economic Review. Vol. 18. No. 1. P. 139–165.
31. Solow R.М. (1957). Technical Change and the Aggregate Production Function // The Review of Economics and Statistics. Vol. 39. No. 3. P. 312–320.
32. WBCPD (2017). World Bank Commodity Price Data (The Pink Sheet). [Электронный ресурс] Режим доступа: http://pubdocs.worldbank.org/en/226371486076391711/CMO-Historical-Data-Annual.xlsx Загл. с экрана. Яз. англ. (дата обращения: 03.05.2017).
33. WBCPD (2019). World Bank Commodity Price Data (The Pink Sheet). [Электронный ресурс] Режим доступа: http://pubdocs.worldbank.org/en/226371486076391711/CMO-Historical-Data-Annual.xlsx Загл. с экрана. Яз. англ. (дата обращения: 01.07.2019).

ГОСТ	Афанасьев А. А. , Пономарева О. С. Народнохозяйственная производственная функция России в 1990—2017 гг. // Экономика и математические методы. – 2020. – T. 56. – Номер 1 C. 67-78 . URL: https://emmras.ru/s042473880006708-7-1/?version_id=12196. DOI: 10.31857/S042473880006708-7
MLA	Afanasiev, Anton, Ponomareva, Olga "The Macroeconomic Production Function of Russia in 1990–2017." Economics and the Mathematical Methods. 56.1 (2020).:67-78. DOI: 10.31857/S042473880006708-7
APA	Afanasiev A., Ponomareva O. (2020). The Macroeconomic Production Function of Russia in 1990–2017. Economics and the Mathematical Methods. vol. 56, no. 1, pp.67-78 DOI: 10.31857/S042473880006708-7

ООНЭкономика и математические методы Economics and the Mathematical Methods

Народнохозяйственная производственная функция России в 1990—2017 гг.

Вы можете

Библиография

Индексирование

ООНЭкономика и математические методы Economics and the Mathematical Methods

Народнохозяйственная производственная функция России в 1990—2017 гг.

Вы можете

Библиография

Индексирование

Войти через